二叉搜索树

二叉搜索树的概念
二差搜索树结构设计
二叉搜索树的操作以及实现
- 遍历
- 判空
- 插入
- 查找
- 删除(☆☆☆)
- 二叉搜索树的其他方法
二叉搜索树的应用
二叉搜索树的性能分析
二叉树习题练习
AVL树
- AVL树的概念
- AVL树的结构设计
- AVL树的插入(非常重要)
- - AVL树的旋转(☆☆☆☆☆)
  - AVL树的插入操作的代码
  - 代码中的细节
- AVL树的性能

二叉搜索树的概念

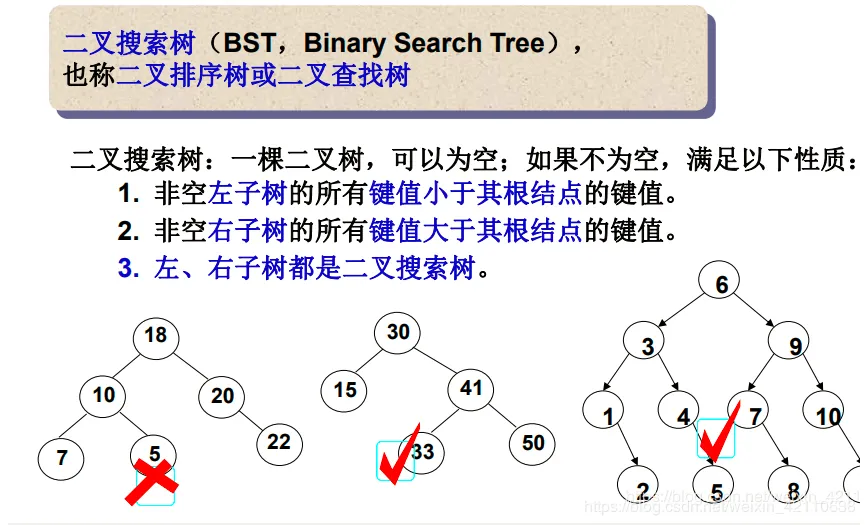
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

二差搜索树结构设计

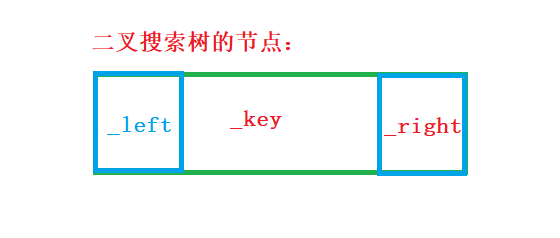
首先我们肯定需要一个节点：

其中_key的数据类型可以是任意数据类型，因此，我们可以将二叉搜索树的节点设置成一个模板类：

	template<class K>
	class BSNode
	{
	public:
		BSNode(const K& key = K())
			:_key(key),_left(nullptr),_right(nullptr)
		{}
		~BSNode()
		{}
	public:
		K _key;
		BSNode<K>* _left;
		BSNode<K>* _right;
	};

同理二叉搜索树，我们也要设计成模板类：

template<class K>
	class BinarySearchTree
	{
	public:
		typedef BSNode<K> Node;
		BinarySearchTree(Node* root = nullptr) :
			_root(root) {}
			
			//function code……
			
	private:
		Node* _root;
	};

二叉搜索树的操作以及实现

遍历

二叉搜索树的遍历，我们一般使用的是中序遍历，因为这种方式遍历出来的结果，一定是有序的：
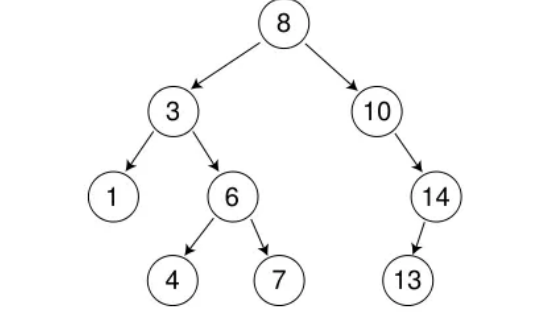
在这里插入图片描述
对于中序遍历，我们不在过多赘述，直接上代码：

public:
void InOrder()//将这个接口暴露给用户，然后隐藏真正的_inOrder接口
		{
			//为什么要封装这一层呢？
			//主要是因为，我们像实现：对象.Inorder()的方式来直接调用，不想在传入参数，况且
			//_root是私有变量，在类外我们也不好获取，就算获取到了，也会感觉写法不够优雅；
			//_root设置为私有的话，又会破坏其封装性
			_InOrder(_root);
			cout << endl;
		}
private:
void _InOrder(Node* root)
{
	if (root == nullptr)
		return;
	_InOrder(root->_left);
	cout << root->_key << " ";
	_InOrder(root->_right);
}

上面是递归写法，简直小意思啦，我们玩一个稍微难一点的，我们可以用非递归的方式来实现二叉树的中序遍历：

//中序遍历非递归写法
void InOrderNR()const
		{
			Node* cur = _root;
			std::stack<Node*> st;
			while (cur!=nullptr||st.empty()==false)
			{
				while (cur)
				{
					st.push(cur);
					//先访问左子树
					cur = cur->_left;
				}
				//访问根
				std::cout << st.top()->_key << " ";
				//访问右子树
				cur = st.top()->_right;
				st.pop();
			}
			std::cout << std::endl;
		}

思路：
1、将cur这课树的左路节点全部入栈；
2、访问栈顶元素；
3、开始访问栈顶元素的右子树(cur=st.top()->_right),并弹栈；

既然都到这了，我们随便也把前序遍历、后序遍历的非递归版本也写一下

//前序遍历非递归
void PreOrderNR()const
{
	Node* cur = _root;
	std::stack<Node*> st;
	while (cur != nullptr || st.empty() == false)
	{
		while (cur)
		{
			st.push(cur);
			//先访问根
			std::cout << cur->_key << " ";
			//再访问左子树
			cur = cur->_left;
		}
		//开始访问右子树
		cur = st.top()->_right;
		st.pop();
	}
	std::cout << std::endl;
}

思路:
1、将cur这课树的左路节点全部入栈，在入栈的同时访问cur节点；
2、访问栈顶元素的右子树(cur=st.top()->_right),弹栈；

//后序遍历非递归
void PostOrderNR()const
{
	Node* cur = _root;
	Node* prev = nullptr;//记录上一次访问的节点
	std::stack<Node*> st;
	while (cur != nullptr || st.empty() == false)
	{
		while (cur)
		{
			st.push(cur);
			//访问左子树
			cur = cur->_left;
		}
		//开始访问栈顶元素的右子树
		//1、如果右子树为空，或者被访问过了，那就直接访问根
		if (st.top()->_right == nullptr || prev == st.top()->_right)
		{
			prev = st.top();
			std::cout << st.top()->_key << " ";
			st.pop();
		}
		else
		{
			//2、如果右子树不为空，也没有被访问过，那么就开始访问右子树
			cur = st.top()->_right;
		}
	}
	std::cout << std::endl;
}

思路：
1、将cur这课树的左路节点全部入栈；
2、访问栈顶元素的右子树，在访问之前，我们可以先比较一下:
①如果栈顶元素的右子树为空树(st.top()->_right ==nullptr) 或者说栈顶元素的右子树我们已经访问过了(prev ==st.top()->_right)，那么说明栈顶元素的右子树，已经不值得我们再去访问了，我们直接访问栈顶元素就好了，然后弹栈；
②如果前面的两个条件都不满足，那么说明栈顶元素的右子树还没有被访问过，我们就需要先去访问栈顶元素的右子树(cur=st.top()->_right);

判空

bool empty()const
{
		return _root == nullptr;
}

插入

根据二叉搜索树的性质，我们可以很轻松的写出插入的操作：

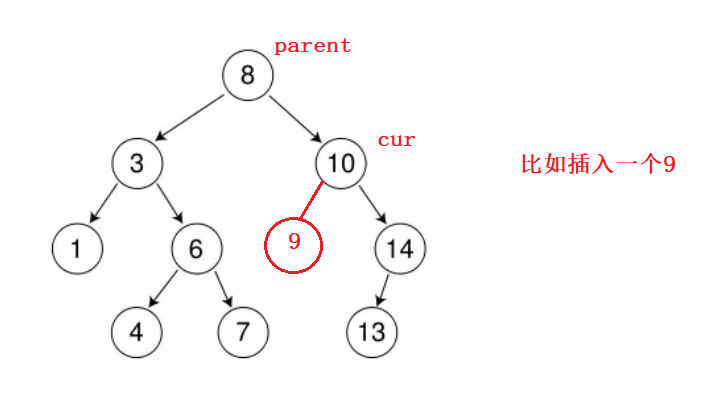
在这里插入图片描述
搜索二叉树，不允许插入重复的元素，如果重复元素插入，那么表面此次插入失败；

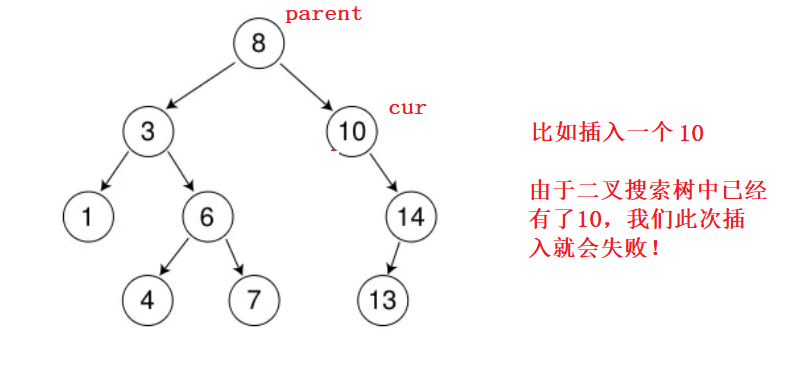
bool insert(const K& key)
{
	//如果是首次插入,那么直接更新_root
	if (_root == nullptr)
	{
		_root= new Node(key);
		return true;
	}
	Node* cur = _root;
	Node* parent = nullptr;//记录一下cur的父亲，方便以后链接
	while (cur)
	{
		parent = cur;//在cur往后走之前先记录一下cur
		if (cur->_key > key)//要插入的节点，比cur->_key小，所以我们应该插在cur的左子树
		{
			cur = cur->_left;
		}
		else if (cur->_key < key)//要插入的节点，比cur->_key大，所以我们应该插在cur的右子树
		{
			cur = cur->_right;
		}
		else//二叉搜索树不允许插入重复元素，插入失败 
		{
			return false;
		}
	}
	//找到了插入位置
	Node* NewNode = new Node(key);
	//判断一下该插入parent的左孩子，还是右孩子
	if (key < parent->_key)
	{
		//插入parent的左子树
		parent->_left = NewNode;
	}
	else
	{
		//插入parent的右子树
		parent->_right = NewNode;
	}
	return true;
}

递归版本的插入:

bool insertR(const K& key)
{
	return _insertR(_root, key);
}
//这里注意root的类型，是指针的引用，这里很巧妙,避免了设计多个参数的困扰，
//这里的root有两层含义:
//1、在空间上，root引用的是上一个节点的_left域或者_right域；
//2、在存储内容上，是本层节点的地址；
bool _insertR(Node*& root, const K& key)
{
	//找到了要插入的位置
	if (root == nullptr)
	{
		Node* newNode = new Node(key);
		root = newNode;
		return true;
	}
	//插入失败
	if (root->_key == key)
		return false;
		//插在cur的左子树
	if (root->_key > key)
		return _insertR(root->_left, key);
	else//插在cur的右子树
		return _insertR(root->_right, key);
}

查找

查找的思想与插入一样，就不在过多赘述:

Node* find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		Node* parent = cur;//记录一下key的父亲
		if (cur->_key > key)//cur往左走
			cur = cur->_left;
		else if (cur->_key < key)
			cur = cur->_right;
		else//找到这个节点了
			return cur;
	}
	return nullptr;//没找到
}

递归版本：

Node* findR(const K&key)//递归版本的查找
{
	return _findR(_root,key);
}
Node* _findR(Node* root, const K& key)
{
	if (root == nullptr)
		return nullptr;
	if (root->_key == key)
		return root;
	if (root->_key > key)
		return _findR(root->_left, key);
	else
		return _findR(root->_right, key);
}

删除(☆☆☆)

二叉搜索树的删除，是比较复杂的，因为根据被删除的节点的类型不同，我们有着不同的删除方法；
为此我们可以对这些情况进行分类：
1、假设被删除的节点是个叶子节点；
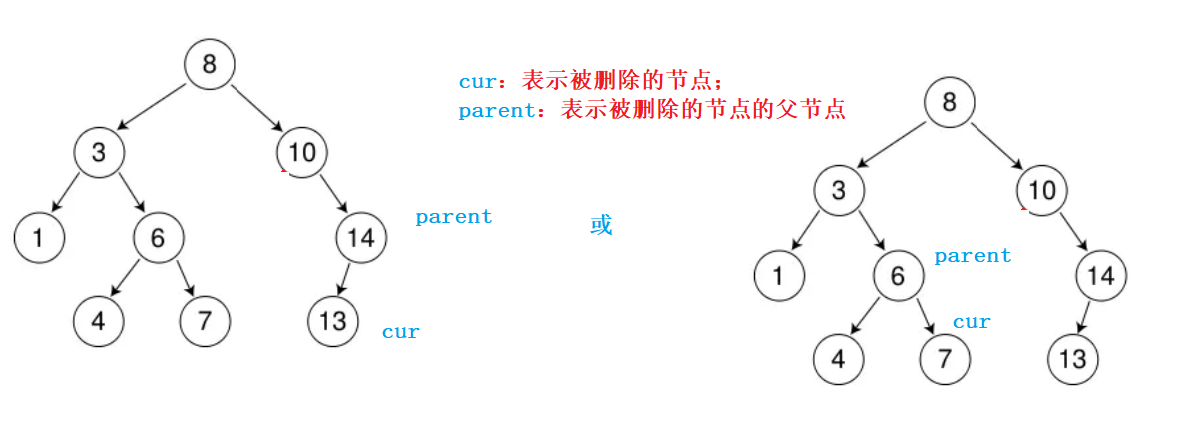
在这里插入图片描述

解决办法：

先判断cur是parent的左孩子还是右孩子节点，然后将对应的parent节点的_left域或_right域置空；
最后释放cur节点；

2、 假设被删除的节点是度为1的节点

其中度为1的节点，还可以细分为：左孩子为空&&右孩子不为空、右孩子为空&&左孩子不为空，这两种情况；我们来具体讨论一下：
①左孩子为空&&右孩子不为空
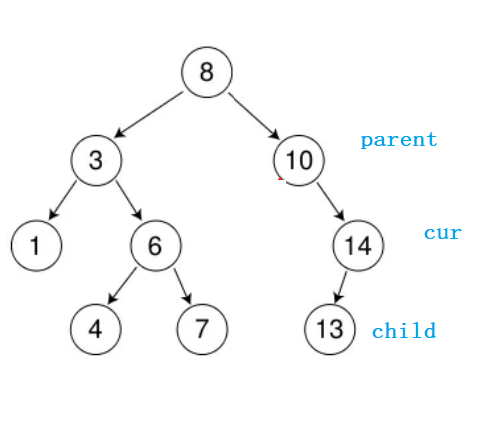
在这里插入图片描述
如此看来，cur节点既然度为1，那么必然存在后代对吧，而且这个后代我们可以很轻松的找到对吧！
我们就用child来表示cur节点的后代吧；
由于现在我们讨论的cur是左孩子为空&&右孩子不为空，那么cur节点的右孩子一定存在对吧，那么child=cur->_right;这一定是成立的吧！
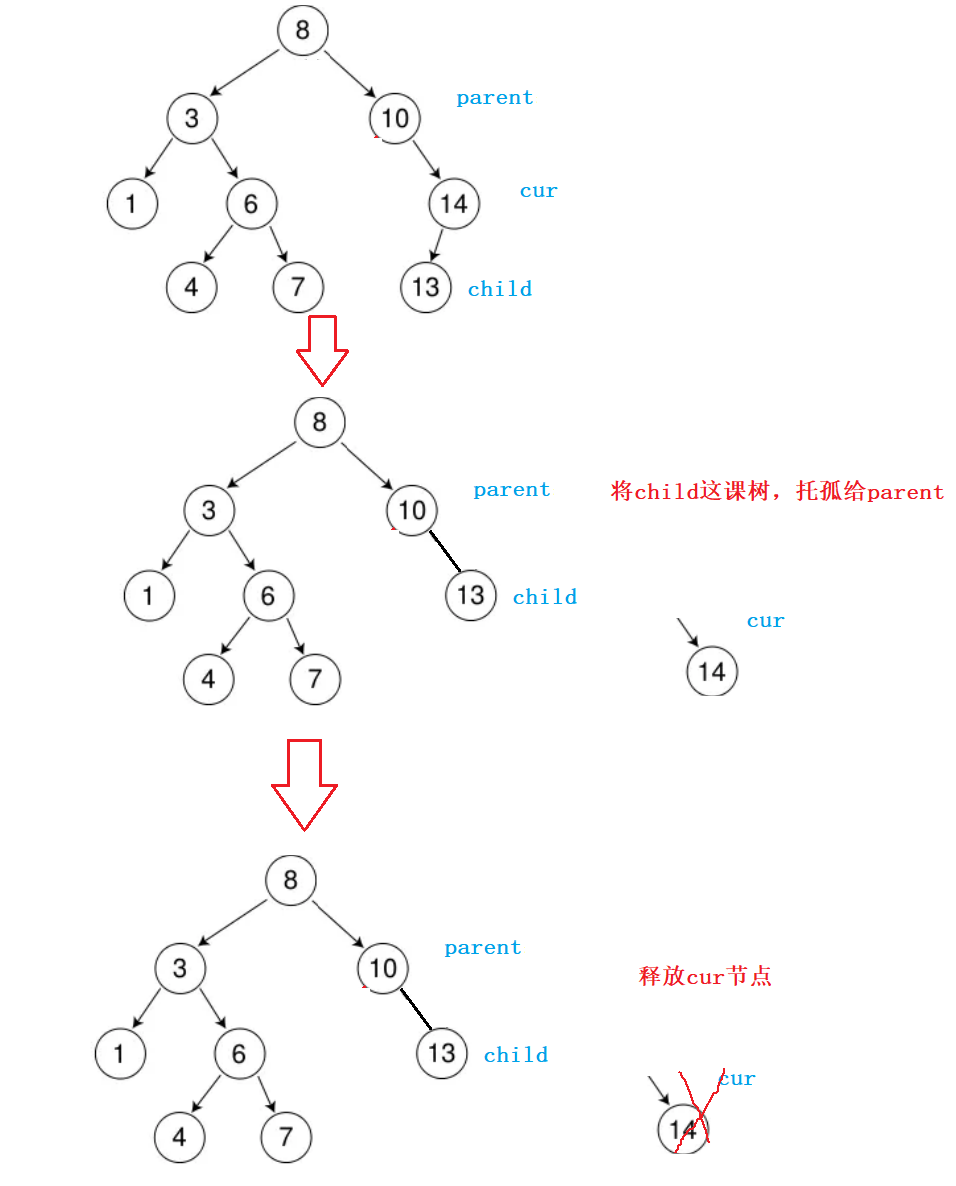
因此我们现在我们要做的就是“托孤”,cur不是马上要被删除了，在cur节点被删除之前，我们先把cur的孩子托付给parent，可是到底是托付给parent的右边还是左边呢？
这是我们需要判断的：
如果cur->_key< parent->_key,说明cur是parent的左孩子，作为cur的孩子，child自然应该链接在parent的左边；
如果cur->_key > parent->_key,说明cur是parent的右孩子，作为cur的孩子，child自然应该链接在parent的右边；
随后完成“托孤”这一壮举过后，我们便可以让cur顺利的“驾崩”了；
在这里插入图片描述
②右孩子为空&&左孩子不为空

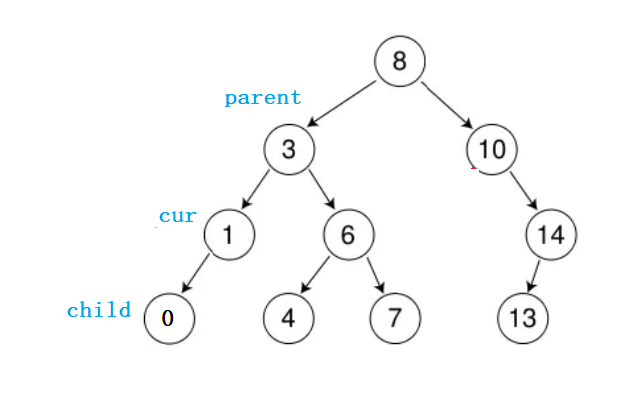
在这种情况下，cur节点的左孩子一定存在，我们需要先保存一下cur节点的左孩子，就用child来表示；
接着，我们再将cur的孩子“托孤”给parent节点，具体是托孤给parent的右边还是左边：我们需要进行判断：
如果cur->_key < parent-> _key,说明cur是parent的左孩子，作为cur的孩子，child自然应该链接在parent的左边；
如果cur->_key > parent->_key,说明cur是parent的右孩子，作为cur的孩子，child自然应该链接在parent的右边；
紧接着，我们在释放cur节点，就顺利的完成了本次节点的删除！
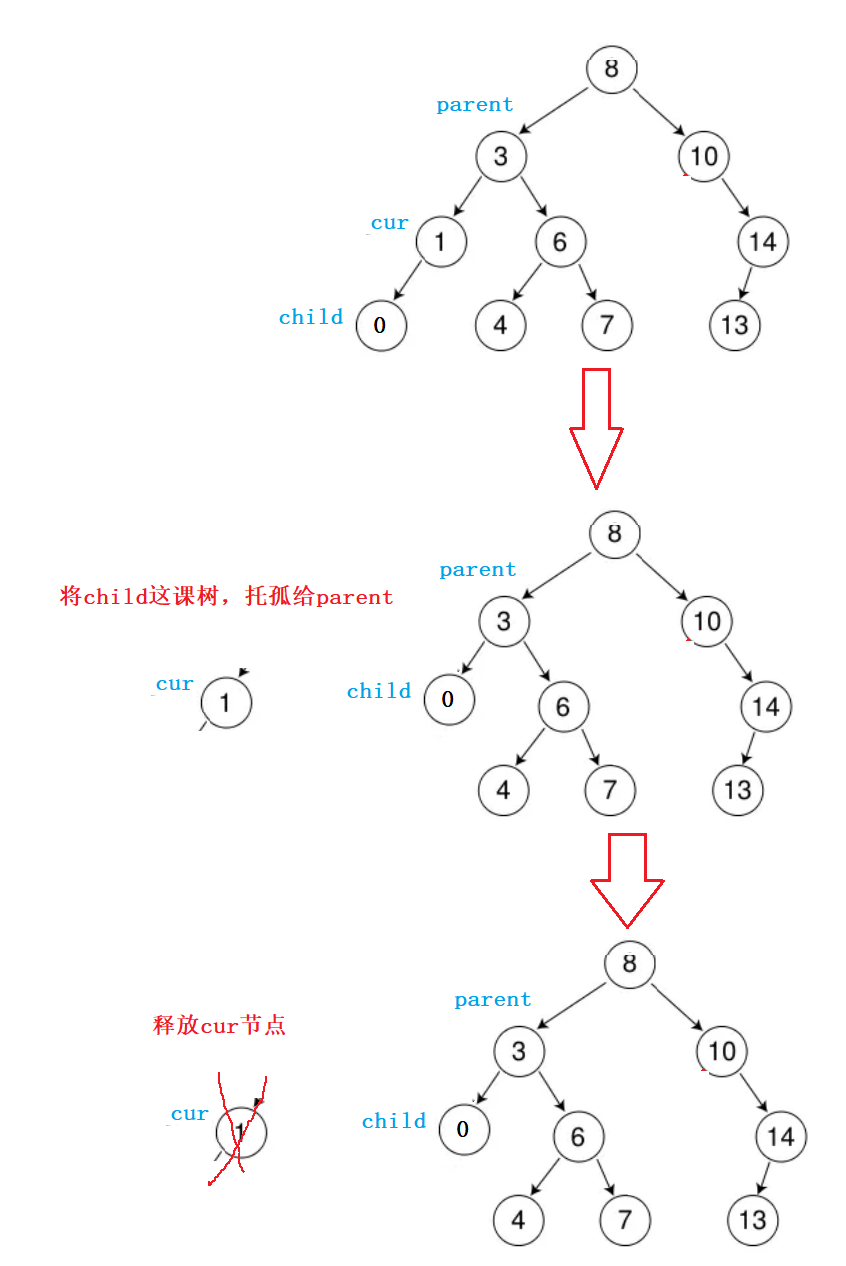
在这里插入图片描述
综上所述：
我们可以发现：左孩子为空&&右孩子不为空、右孩子为空&&左孩子不为空，这两种情况的处理方式非常相同！

解决办法：

找到cur的后代（child）；
根据cur在parent的左边还是右边，将child正确的“托孤”给parent；
释放cur节点；

3、假设被删除的节点是度为2的节点
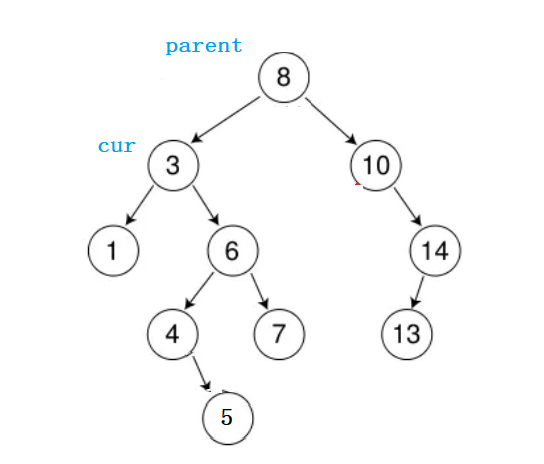
在这里插入图片描述
对于这种节点的删除，我们所采取的办法是：“狸猫换太子”+“托孤” 这两者相结合；
如何个“狸猫换太子”？切听我慢慢道来：
cur不是一个度为2的节点嘛，那么他的右孩子一定存在对吧！
我们就暂且将，cur的右孩子用CurRight来表示吧：
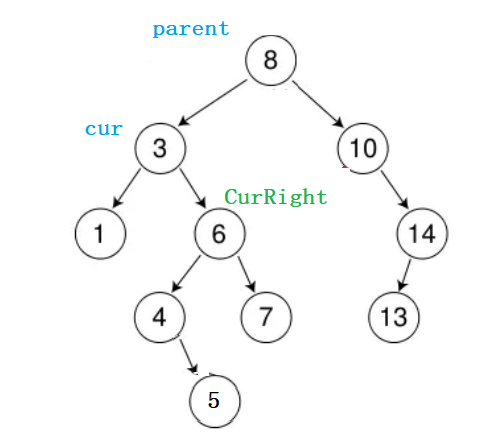
在这里插入图片描述
现在，我们将CurRight这课子树与原树剥离开来（逻辑层面上的剥离），那么CurRight是不是就是一颗独立的子树了，好，我们在去CurRight这课树中寻找最小值寻找，我们暂且用RightMin来记录吧，同时使用PRightMin来记录RightMin节点的父节点，
最开始的时候:RightMin=CurRight,PRightMin=nullptr;
在一颗二叉搜索树中寻找这课树的最小值，那么这个最小值一定在这课树的最左边不是！所以我们只要一直往左边走就能找到CurRight这课树的最小值了：

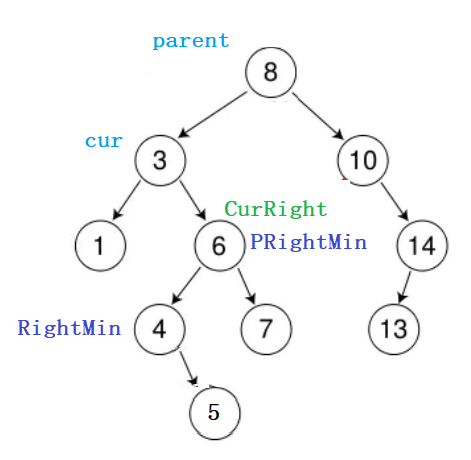
在这里插入图片描述
走到这里过后，我们在保存一下，RightMin节点的后代，RightMin节点一定是这课树的最小节点，同时也是这课树的最左节点，那么RightMin节点一定是一个度为0或者度为1的节点，我们不管他到底是那种情况，我们先保存就对了，我们用RightMin_child来记录RightMin节点的孩子：
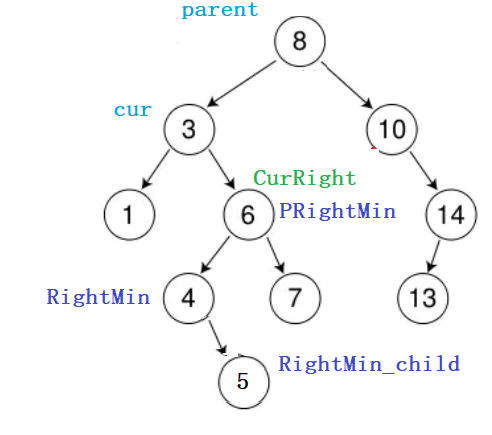
在这里插入图片描述
做完这一切准备，我们的好戏就要开场了：
我们交换cur节点与RightMin节点的 _key值，然后利用“托孤”的办法，删除RightMin节点，你看看，我们是不是就顺利的完成了本次删除：

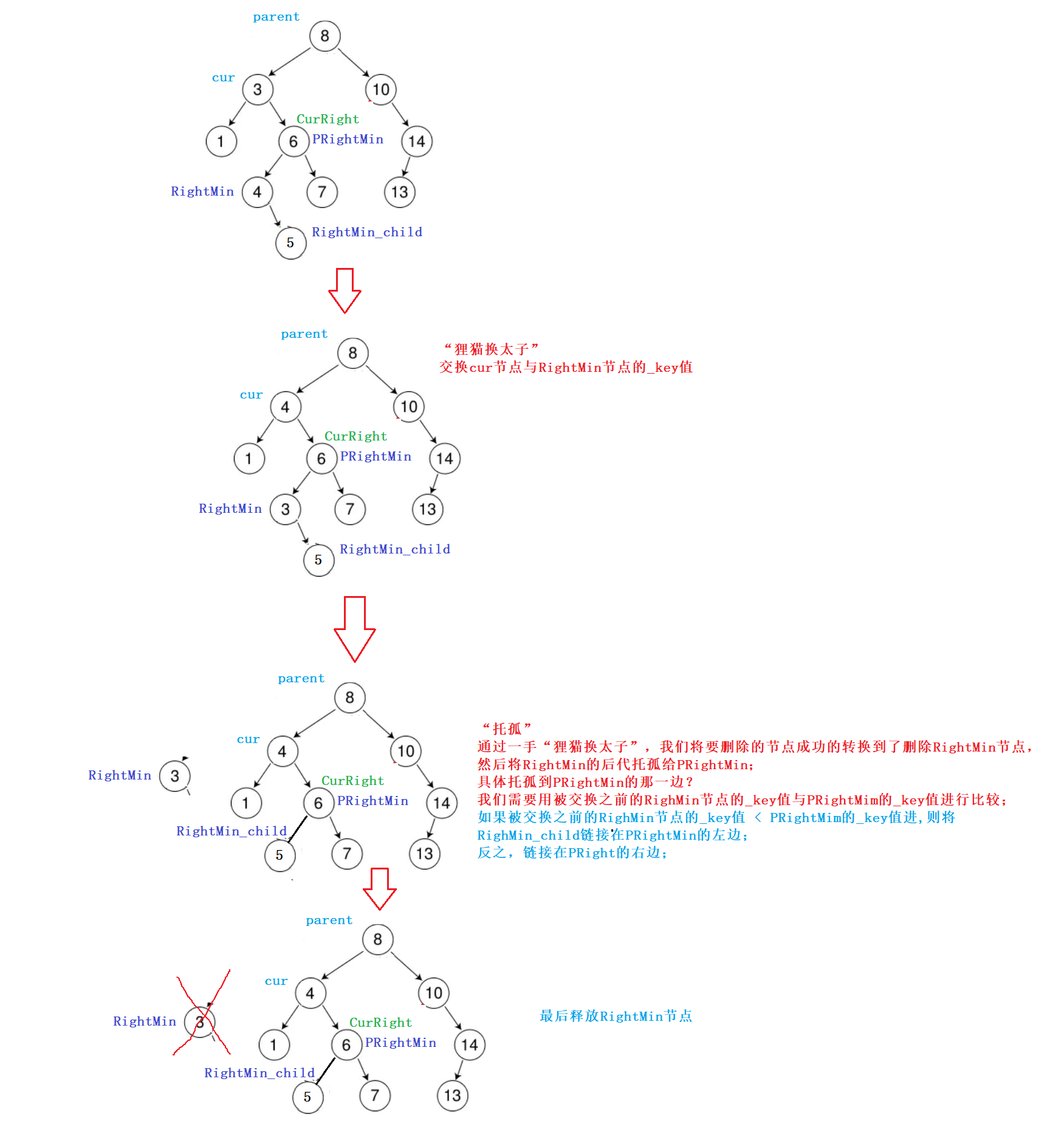
解决办法：

先找到cur这个节点的右子树，记作CurRight
在CurRight这课树中，找到这课树中的最小节点及其父亲节点，分别记作：RightMIn、>PRightMin，然后在保存一下RightMin这个节点的右子树，暂且记作RightMin_child;
交换cur节点与RightMin_child节点的_key值；
将RightMin_child这课树托孤给PRightMin这课树；
释放RightMin这个节点；

好了，我们讨论完了，所有被删除的节点的情况，因此，根据这几种情况，我们就用代码来实现一下把，当然，上面的只是大体思路，还有一些细节，我们需要在代码中具体处理一下:

bool erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
	if (cur->_key < key)
	{
		parent = cur;
		cur = cur->_right;
	}
	else if (cur->_key > key)
	{
		parent = cur;
		cur = cur->_left;
	}
	else//被删除的节点，找到了
	{
		//细节1：实际上，我们按照我们刚才的理论总共有3中情况，但是实际上第一种情况与第二种
		//情况实际上是可以合并在一起的，我们可以假设叶子节点的孩子为空树嘛，空树也是树！
		//因此，实际的删除情况只有2种！
		if (cur->_left == nullptr || cur->_right == nullptr)
		{
			Node* child = nullptr;
			//提前记录一下被删除的节点的孩子
			if (cur->_right == nullptr)//右孩子为空&&左孩子不为空
				child = cur->_left;
			else//左孩子为空&&右孩子不为空
				child = cur->_right;
			//细节2：我们之前讨论的删除节点cur都是建立在cur的parent节点存在的情况之上
			//要是万一，cur没有父亲节点呢？（parent=nullptr）
			//谁没有父亲？根节点！因此，我们的child没有parent可以托付
			//我们的child就只能，立马继位了，成为新一代的“王”
			if (cur == _root)//被删除节点是根节点
				_root = child;
			else//被删除节点不是根节点，直接托孤
				//child托给parent的右边
				if (cur->_key > parent->_key)
					parent->_right = child;
				else//child托给parent的左边
					parent->_left = child;
			delete cur;//释放cur节点
		}
		else
		{
			//cur是度为2的节点
			Node* RightMin = cur->_right;//用于记录cur的右子树中的最小节点
			Node* PRightMin = cur;//用于记录cur的右子树中的最小节点 的父亲节点
			while (RightMin->_left)
			{
				PRightMin = RightMin;
				RightMin = RightMin->_left;
			}
			//找到了右子树最小的节点
			//1、交换cur节点和RightMin的节点的值(狸猫换太子)
			std::swap(cur->_key,RightMin->_key);
			//2、记录RightMin的右孩子
			Node* RightMin_child = RightMin->_right;//记录RightMin的孩子
			//3、将右子树最小节点的右孩子托孤给父亲
			//这里我们把右子树“剥离”整颗树来看，RightMin节点有无父节点
			if (PRightMin == cur)//说明在cur->_right整颗右子树中没有RightMin节点的父节点,我们需要将RIghtMin的孩子托付给cur的右边
				PRightMin->_right = RightMin_child;
			//RIghtMIn在cur->right这课树中有父节点
			//直接将孩子节点托给PRightMin节点的左边
			else
				PRightMin->_left = RightMin_child;
			delete RightMin;//释放RightMin节点
		}
		return true;
	}
}
//没找到要删除的节点，直接删除失败
return false;
}

上面是，非递归版本，我们再来搞一搞递归版本：

bool eraseR(const K&key)
{
	return _eraseR(_root,key);
}
//注意这里，采用的root的引用，非常的巧妙!
bool _eraseR(Node*& root, const K&key)
{
	if (root == nullptr)
		return false;
	if (root->_key == key)
	{
		//a.被删除的节点度为0或度为1
		if (root->_left == nullptr || root->_right == nullptr)
		{
			Node* del = root;
			Node* child = nullptr;
			if (root->_left == nullptr)
				child = root->_right;
			else
				child = root->_left;
			root = child;
			delete del;
		}
		else//b.被删除的节点度为2
		{
			//1、先找到右子树中最小的节点
			Node* RightMin = root->_right;
			Node* PRightMin = root;
			while (RightMin->_left)
			{
				PRightMin = RightMin;
				RightMin = RightMin->_left;
			}
			//找到啦
			std::swap(root->_key, RightMin->_key);
			//将我们要删除掉值转换到右子树中，这样问题就变成了删除右子树中的最小节点
			//这里的话，我们要把root->_right剥离开来看,这样才能更清晰
			_eraseR(root->_right,key);
		}
		return true;
	}
	if (root->_key > key)
		return _eraseR(root->_left, key);
	else
		return _eraseR(root->_right,key);
}

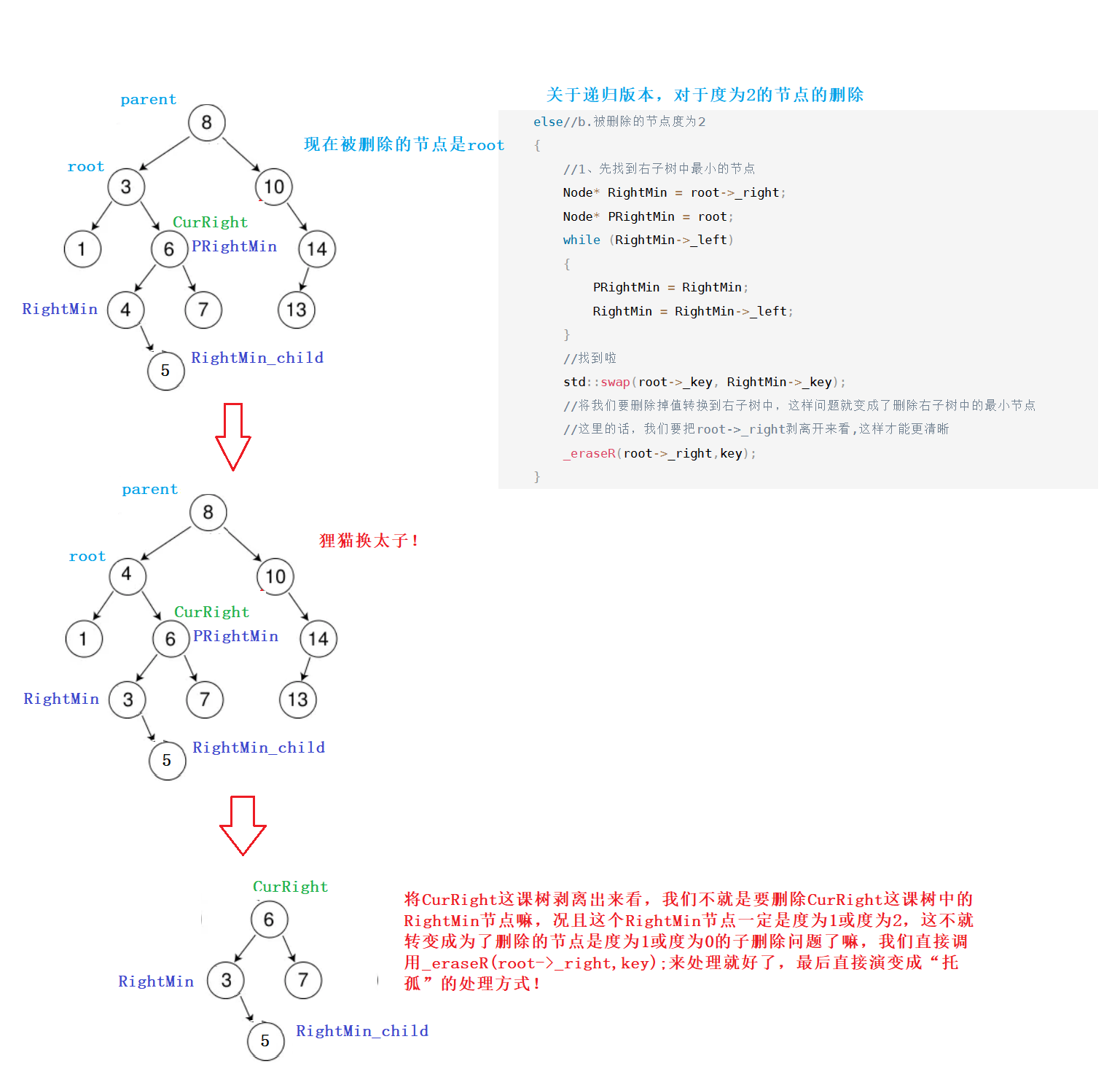
在这里插入图片描述
二叉搜索树的删除测试
如果，你看明白了，那我觉得这件事：
**泰裤啦！**

二叉搜索树的其他方法

二叉搜索树，坑定是要进行深拷贝的，因此，我们需要重载一下operator=和重写拷贝构造函数：

//拷贝构造实现
BinarySearchTree(const BinarySearchTree<K>& bst)
{
	_root=copy(bst._root);
}
Node* copy(Node* root)
{
	if (root == nullptr)
		return nullptr;
	Node* head = new Node(root->_key );
	head->_left = copy(root->_left);
	head->_right = copy(root->_right);
	return head;
}
//赋值元素符
BinarySearchTree<K>&operator=(BinarySearchTree<K>  bst)
{
	std::swap(_root, bst._root);
	return*this;
}

当然，析构也是少不了的：

//利用层序遍历来进行析构
~BinarySearchTree()
{
	std::queue <Node*> q;
	if (_root)
	{
		q.push(_root);
		while (q.empty()==false)
		{
			Node* root = q.front();
			q.pop();
			if (root->_left)
				q.push(root->_left);
			if (root->_right)
				q. push(root->_right);
			delete root;
		}
	}
}

二叉搜索树的应用

K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到
的值。
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误
KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方
式在现实生活中非常常见：
比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英
文单词与其对应的中文<word, chinese>就构成一种键值对；
再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出
现次数就是<word, count>就构成一种键值对。

二叉搜索树的性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能；
理想情况下，搜索二叉树接近完全二叉树查找的效率是高度次，也就是O( $log_2 N$ );
最差情况下，搜索二叉树退化为单支树，其查找效率为O(N);
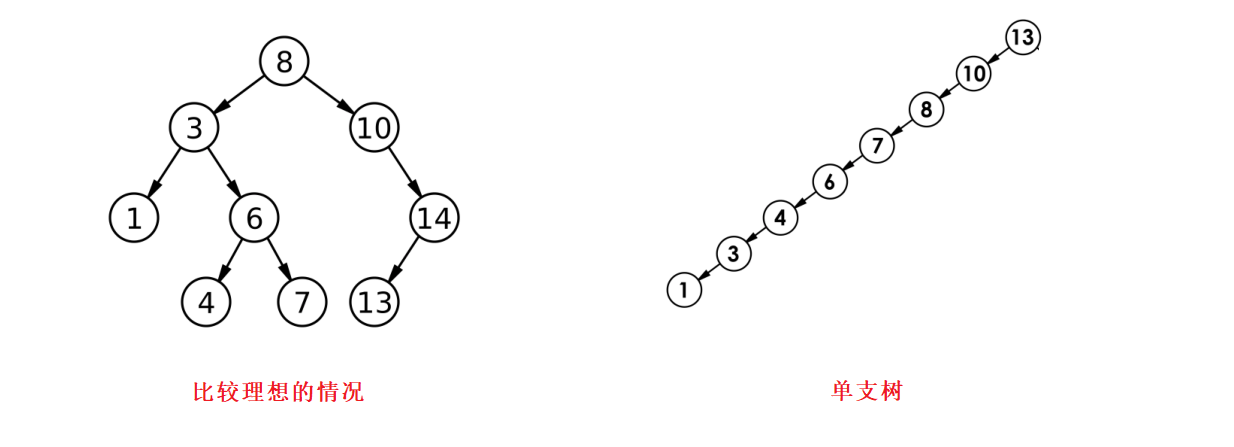
在这里插入图片描述
为此，有没有什么办法来解决单支树的查找问题呢？
答案是有的，AVL树就是专门用来解决这种单支树所带来的效率问题的；

二叉树习题练习

二叉树创建字符串。OJ链接
二叉树的分层遍历1。OJ链接
二叉树的分层遍历2。OJ链接
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。OJ链接
二叉树搜索树转换成排序双向链表。OJ链接
根据一棵树的前序遍历与中序遍历构造二叉树。 OJ链接
根据一棵树的中序遍历与后序遍历构造二叉树。OJ链接
二叉树的前序遍历，非递归迭代实现。OJ链接
二叉树中序遍历，非递归迭代实现。OJ链接
二叉树的后序遍历，非递归迭代实现。OJ链接

AVL树

AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查
找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii
和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
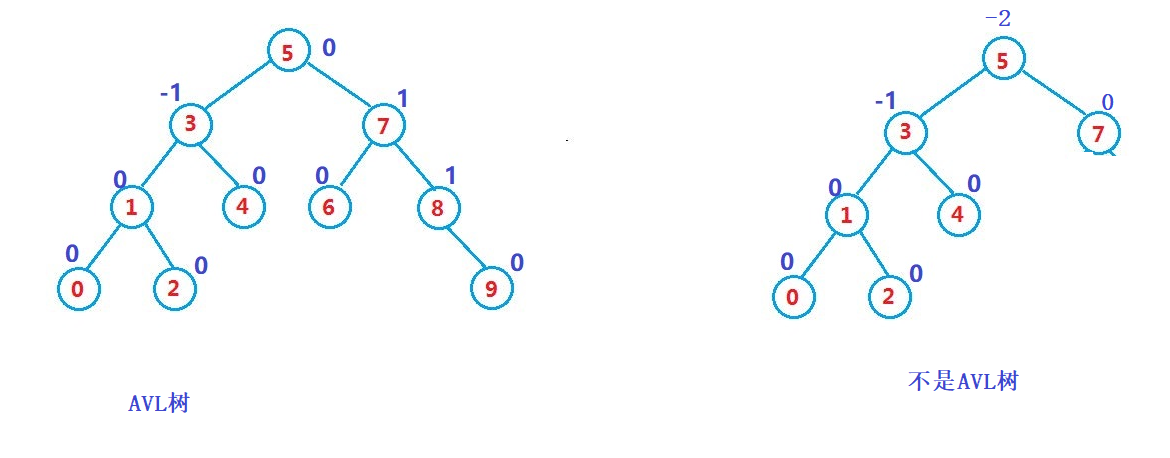
AVL树的定义：

首先是一颗二叉搜索树；
其次是一颗平衡二叉树；或者任一一个节点的左右子树高度差的绝对值都不超过1；
其中，我们把左右子树的高度差叫做平衡因子；
在这里我们规定，平衡因子=右子树的高度-左子树的高度

AVL树的结构设计

//AVL树的节点
template<class K, class V>//直接设置成KV模型，不搞K模型了
	class AVLTreeNode
	{
	public:
		AVLTreeNode(const std::pair<K, V>& p) :
			_data(p),
			_left(nullptr),
			_right(nullptr),
			_parent(nullptr),
			_bf(0)
		{}
		std::pair<K, V> _data;//K、V关系封装在一起
		int _bf;//平衡因子
		AVLTreeNode<K, V> *_left;//
		AVLTreeNode<K, V> *_parent;//用于记录当前节点的父节点
		AVLTreeNode<K, V> *_right;
	};
	//二叉搜索树
	template<class K, class V=bool>
	class AVLTree
	{
		typedef AVLTreeNode<K, V> Node;//节点
	public:
		AVLTree() :_root(nullptr)
		{}
	private:
	Node* _root;
	};

AVL树的插入(非常重要)

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：
1、按照二叉搜索树的方式插入新节点；
2、调整平衡因子的节点；
对于一颗合法的AVL树来说，在AVL树中的每一个节点的平衡因子只有三种情况：-1、0、1；
如果，平衡因子是其它的值，那么说明这并不是一颗合法的AVL树；
当然，上面的一切都是建立在这课树已经是一个二叉搜索树的前提下，才有的；
因此，现在我们向一颗AVL树中插入节点，那么势必会导致AVL树中的某些节点的平衡因子发生改变，为了保证插入节点过后，这课树依旧是一颗AVL树，我们需要对相关节点的平衡因子，进行调整；
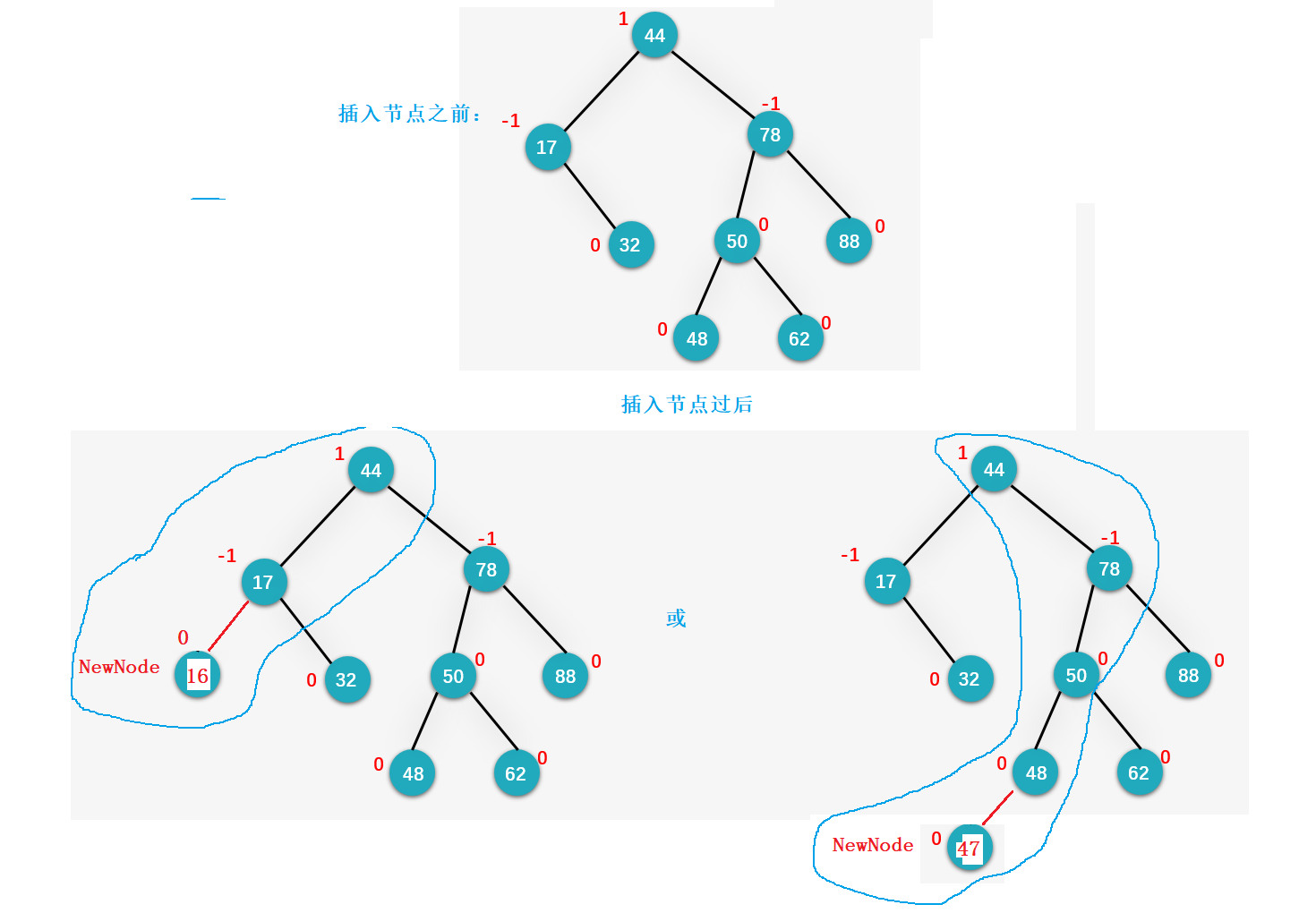
在这里插入图片描述
我们可以发现，当我们插入一个新节点过后，我们必须调整这些节点的平衡因子，哪些节点？
新插入节点的祖先节点的平衡因子！，对于其他节点的平衡因子，我们不必调节，为什么？
根据平衡因子的定义：平衡因子=右子树高度-左子树高度，对于这些除了NewNode节点及其祖先节点之外的节点来说，插入节点前后，这些节点的左子树、右子树的高度根本没有发生变化，平衡因子自然也就不会发生变化，那么我们自然也就不用去关心这些节点的平衡因子；
我们只管调整新插入的节点的祖先节点的平衡因子，由于我们在插入之前这课树就已经是一颗AVL树，因此每一个节点的平衡因子范围是[-1,1]，那么在插入节点过后，我们的祖先节点的平衡因子可能的范围就变成了:[-2,2];
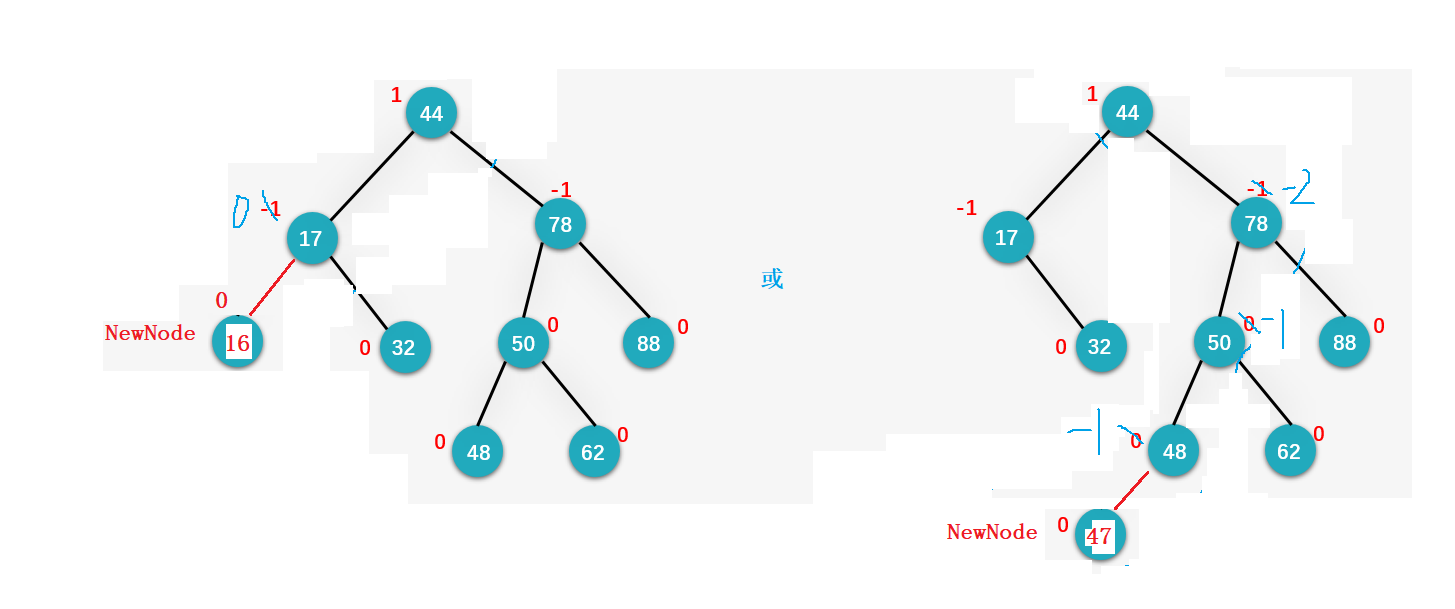
在这里插入图片描述
因此，我们假设NewNode节点的父节点为parent：

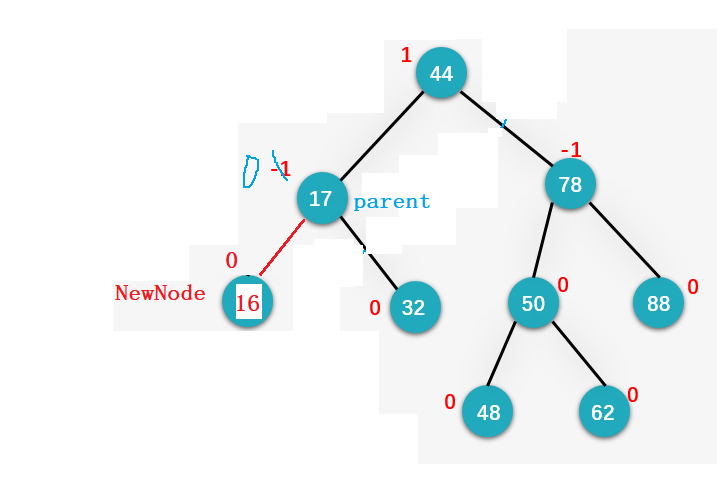
如果，我们插入的节点，在parent这课树的左边的话，那么parent的左子树的高度++，也就是parent->_bf–（因为平衡因子=右-左，现在左边高度+1，自然平衡因子=右 --（左+1））；
如果，我们插入的节点，在parent这课树的右边的话，那么parent的右子树的高度++，也就是parent->_bf++（因为平衡因子=右-左，现在右边高度+1，自然平衡因子=右 +1–左）；
因此，根据parent的更新过后_bf，就会有三种情况，我们就对这三种情况进行讨论：
1、更新过后parent->_bf 的绝对值等于1;
跟新过后parent->_bf 的绝对值等于1，那么说明未插入节点之前，也就是未更新parent节点的平衡因子时，parent节点的平衡因子，一定是0，为什么如此肯定？如何验证我的说法？你凭什么怎么说？
我们可以这样验证：
在这里插入图片描述
这样用数学的方法来证明，就一目了然了，因此就parent这课树来说，现在插入一个节点过后使其右子树-左子树的高度由0变为了-1或1，那么说明插入的节点一定是插在左右子树中任意的那一颗树中的；那么是不是说明在插入节点前后，parent这课树的高度发生了变化！
如果，我们明白了这一点，我们再来讨论，这时要不要继续跟新parent节点的parent节点的平衡因子，也就是是爷爷节点的平衡因子需不需要更新？答案是要的！
为什么，还是根据平衡因子的定义，平衡因子=右子树高度-左子树高度，现在爷爷节点的其中一颗树的高度是肯定不会变的，因为我们并没有向这课树中插入节点，我们是向另一颗树中插入的节点，也就是parent这课树中插入的节点，也就是说要不要更新爷爷节点的平衡因子，完全取决于parent这课树的高度是否变化！那么又如何验证parent这课树的高度是否发生变化？这不就取决于parent节点更新过后的平衡因子，有我们前面的证明可知，parent的平衡因子在更新过后变为了-1或1，这说明parent这棵树的高度发生了变化！因此我们需要继续向上调整爷爷节点，我们需要让parent往上走，向上继续调整平衡因子；
2、 更新过后parent->_bf 的绝对值等于0；

在插入节点过后parent节点的_bf变为了0，那么说明在插入节点之前，parent节点的平衡因子一定是-1或1（证明方法与前面无异），我们在推导一下：在插入节点前后，parent这课树右子树-左子树的高度差由-1或1变成了0，那么说明插入的这个节点一定是插入在parent的左右子树中最矮的一颗，你细品，仔细品！
那么说明，在插入节点前后，parent这课树的高度并没有发生变化，那么说明我们不必再更新爷爷节点及其祖先节点的平衡因子了！此次插入非常成功！很nice！我们可以提前结束本次插入了！

3、 更新过后parent->_bf 的绝对值等于2；

在插入节点过后parent节点的_bf变为了-2或2，那么说明在插入节点之前，parent节点的平衡因子一定是-1或1（证明方法与前面无异），那是不是说明，在插入节点前后，parent这课树右子树-左子树的高度由-1或1变成了-2或2，我们在深入挖掘一下，这个插入的节点是不是一定是插在左右子树中高的一颗子树中的！同时由于此时parent节点的平衡因子已经不满足，我们对于AVL树的要求了，我们必须将parent这课树调整为AVL树，我们所采取的办法就是：旋转！；
因此，我们可以先把AVL树的插入操作的大框架先写出来：

bool insert(const std::pair<K, V>& data)
{
	Node* parent = nullptr;
	Node* cur = _root;
	if (_root == nullptr)//空树
	{
		_root = new Node(data);
		return true;
	}
	while (cur)
	{
		parent = cur;
		if (cur->_data.first == data.first)
			return false;
		else if (cur->_data.first > data.first)
			cur = cur->_left;
		else
			cur = cur->_right;
	}
	cur = new Node(data);
	//记住要维护父指针域
	cur->_parent = parent;
	if (parent->_data.first > cur->_data.first)
		parent->_left = cur;
	else
		parent->_right = cur;
	//插入一个节点过后，必定导致，cur这个节点的祖宗节点的平衡因子改变，我们需要跟新cur的父节点的平衡因子
	while (parent)
	{
		//cur是parent的右子树中的孩子,parent右子树高度++，即:_bf++
		if (cur->_data.first > parent->_data.first)
			parent->_bf++;
		else
			parent->_bf--;
		//检查更新过后的parent的平衡因子，然后做出不同的反应
		if (parent->_bf == 0)
		{
			//更新过后parent的平衡因子为0，那么更新之前parent的平衡因子一定是 ±1 （可列方阵=程验证）;
			//这说明，新插入的节点，是插在parent矮的一颗子树上的，parent这棵树的高度不变，无需在更新祖宗节点的平衡因子;
			//此次插入，非常成功
			break;
		}
		else if (abs(parent->_bf) == 1)
		{
			//更新过后parent的平衡因子是 ±1 那么说明更新之前parent的_bf一定是0
			//这说明在此次插入过后，parent这棵树的高度增加了，必须更新祖宗节点的_bf
			parent = parent->_parent;//parent向上走
		}
		else if (abs(parent->_bf) == 2)
		{
			//旋转
		}
		else
		{
			//如果更新完过后parent->_bf等于1、-1、0、-2、2之外的数，不用说了，插入之前的AVL树就已经出问题了
			assert(false);
		}
	}
	return true;
}

AVL树的旋转(☆☆☆☆☆)

针对parent这课树的情况不同，又衍生出不同的旋转方法！
比如：LL型、RR型、LR型、RL型；
想必这些什么类型我们早就已经烂熟于耳了，只要我们一学到AVL树的旋转，这四种类型就会被老师反复的提出来！
可是！老师们只顾着告诉我们parent树有这4种需要旋转的情况，却没有告诉我们为什么会有这4种旋转情况？这四种情况究竟是怎么来的？这常常会让我们对AVL树的旋转而感到困惑，觉得AVL树的旋转很难！

接下来，我们就来谈一谈为什么AVL树的旋转会有这4种情况，以及这4种旋转是如何得来的：

首先，我们需要明白，我们什么时候需要进行旋转？
当然是更新过后parent-> _bf == -2或2的时候；
我们要旋转什么？
旋转的是parent这课树，不是parent这个节点！
旋转的目的？
①降低parent这棵树的高度；
②保证parent这棵树在旋转过后依旧是一个合法的AVL树；
③让整颗树在旋转过后，由一颗不合法的AVL树变为合法的AVL树！

上面我们已经推出了，是在parent-> _bf == -2或2的时候进行旋转，在未插入节点之前，parent -> _bf等于-1或1，因此我们可以画出未插入节点之前parent这课树的抽象图：
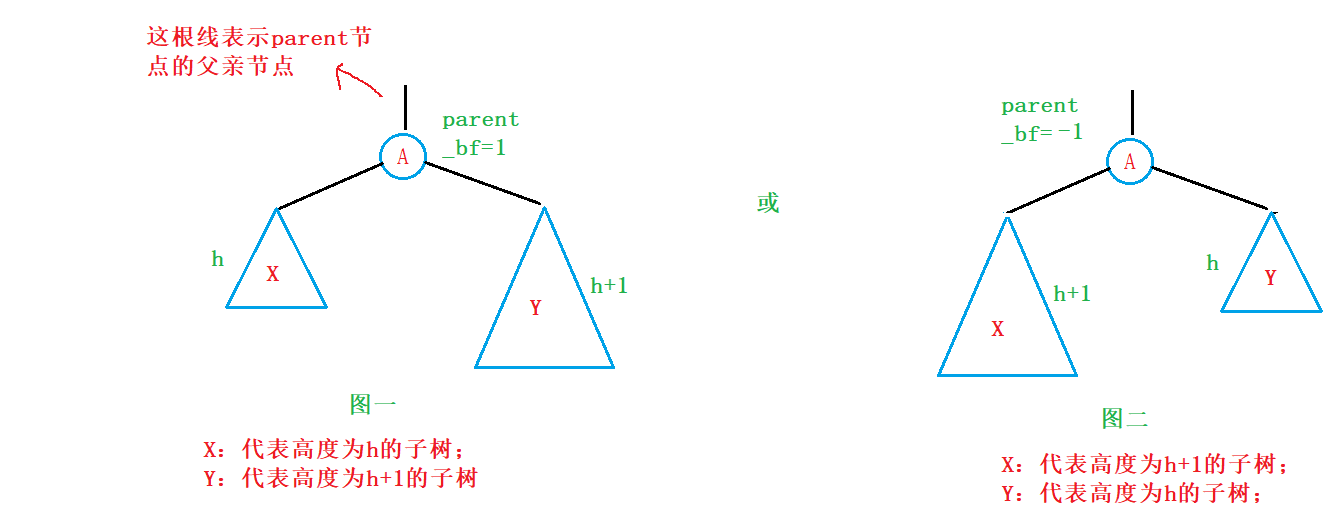
在这里插入图片描述
我们可以看到，根据未插入节点之前，parent节点的_bf 我们可以分别画出两幅对称的抽象图：
因此，对于图一来说：如果我们在插入节点过后想要使parent节点的 _bf 变为-2或2，那么我们只有将节点插入Y树中，只有插入Y树中，parent节点的的 _bf才有可能 变为-2或2，我为什么要加个有可能呢？因为我们在Y树中插入节点过后，并不能不保证Y树的高度变为h+2，也有可能在我们插入节点过后Y树的高度不变还是h+1，这样就不能使parent节点的 _bf 的平衡因子变为2了，但是嘛，至少还有希望！要是我们将节点插入在X树中去，那么parent节点的平衡因子一定不可能变为-2或2，因为在X树中插入节点，X树的高度可能为h或h+1，无论是哪一种情况都不能使parent节点的平衡因子变为-2或2；因此，要使parent节点的平衡因子变为-2或2，那么对于图一这种情况，我们只能将新节点插入在Y树中！
同理，对于图二的这种情况，我们也只能将节点插入在X树中！
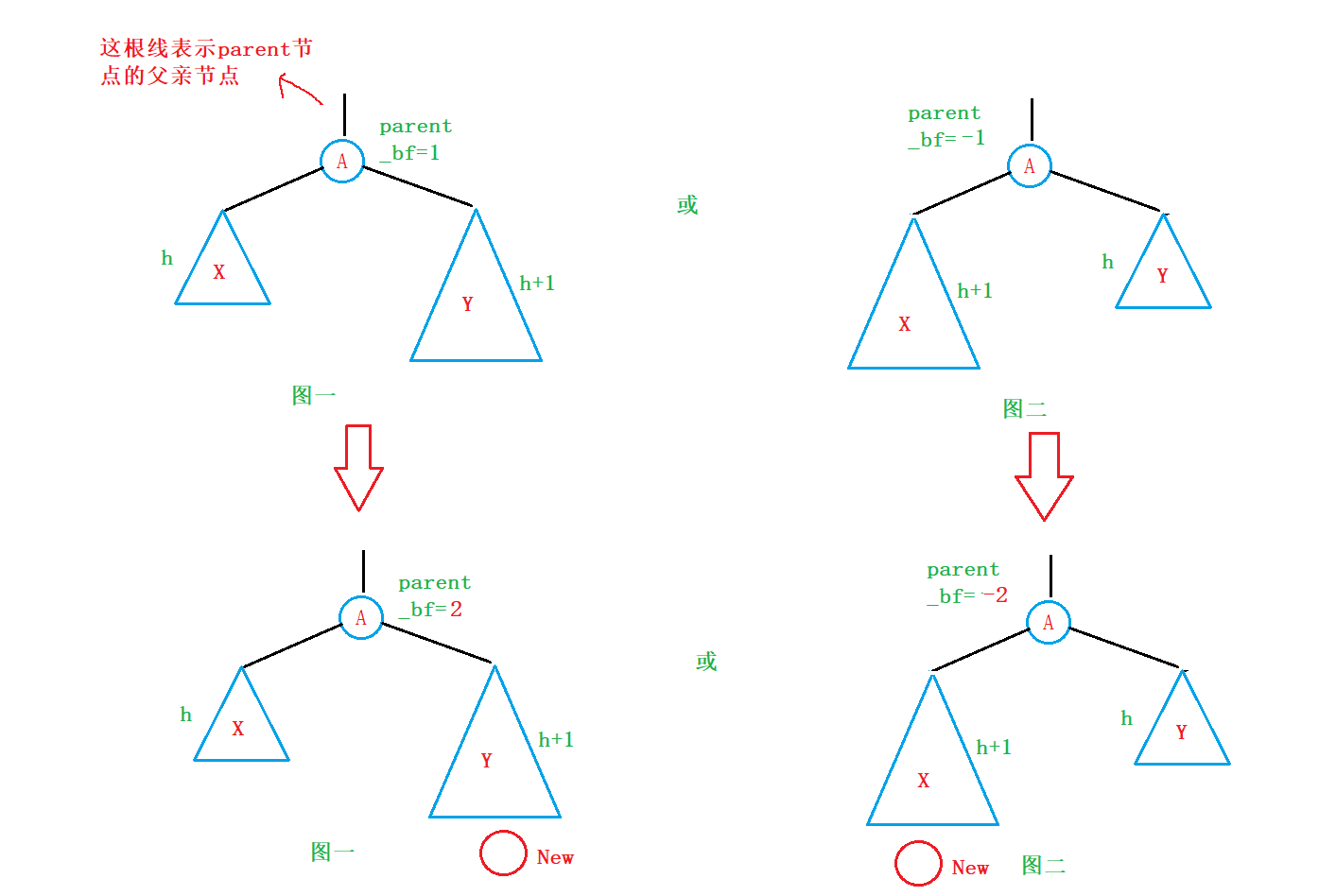
在这里插入图片描述

因此针对这两种不同的情况，我们可以分开讨论：
一、假设插入节点过后，parent-> _bf == 2:
那么这种情况对应这图一的情况：
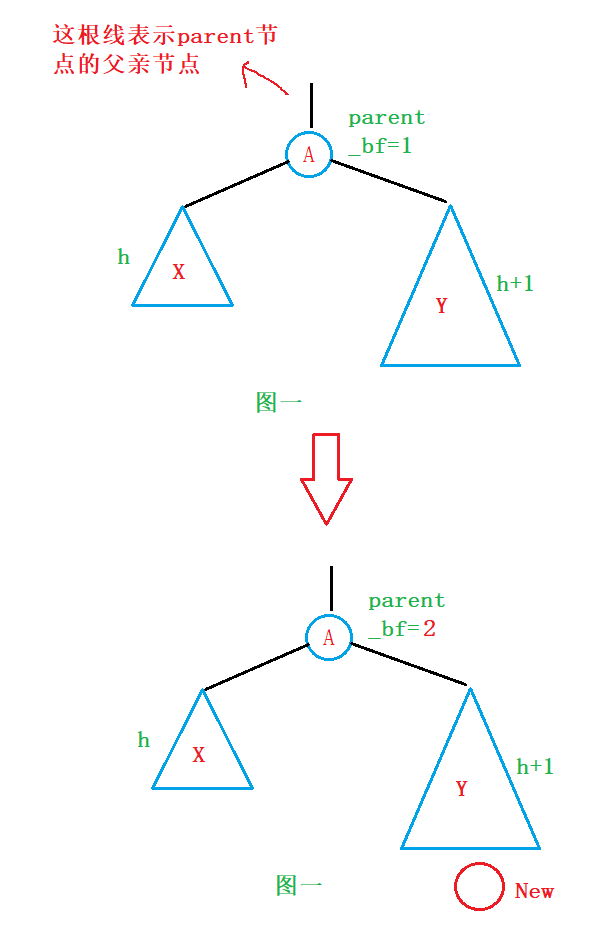
在这里插入图片描述
为了讨论的方便，我们可以做一个等效变换，我们将Y树等效为：

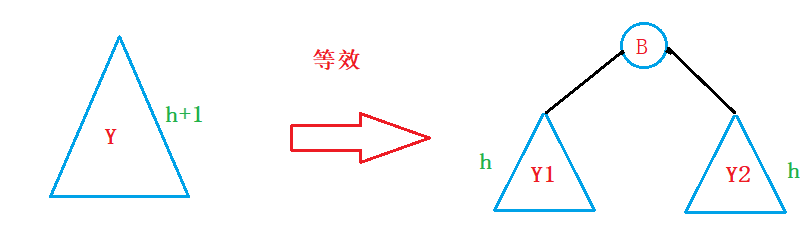
我们将其替换进图一：

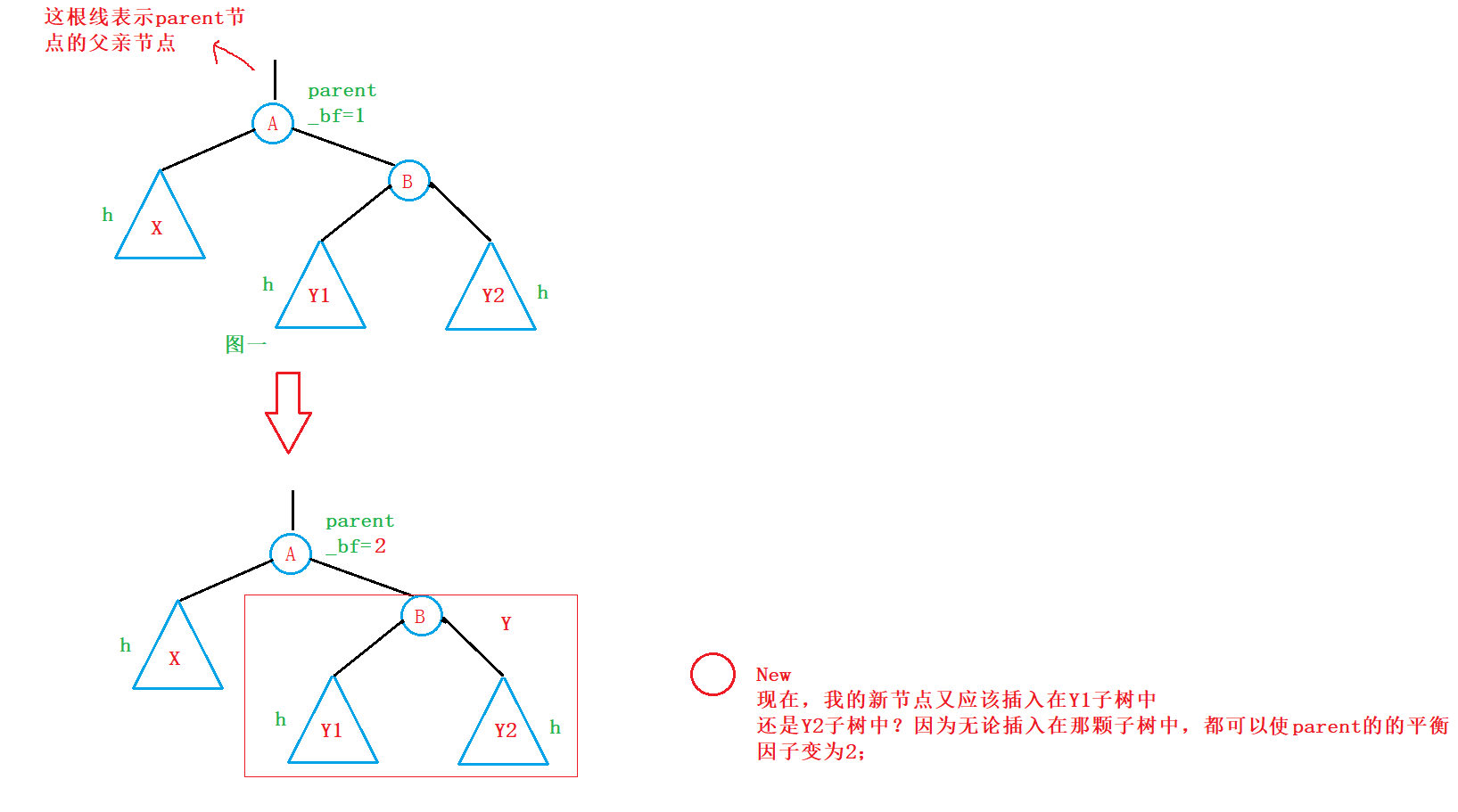
因此，对于新节点，我们是插入Y1子树中，还是Y2子树中，我们又得分开讨论：

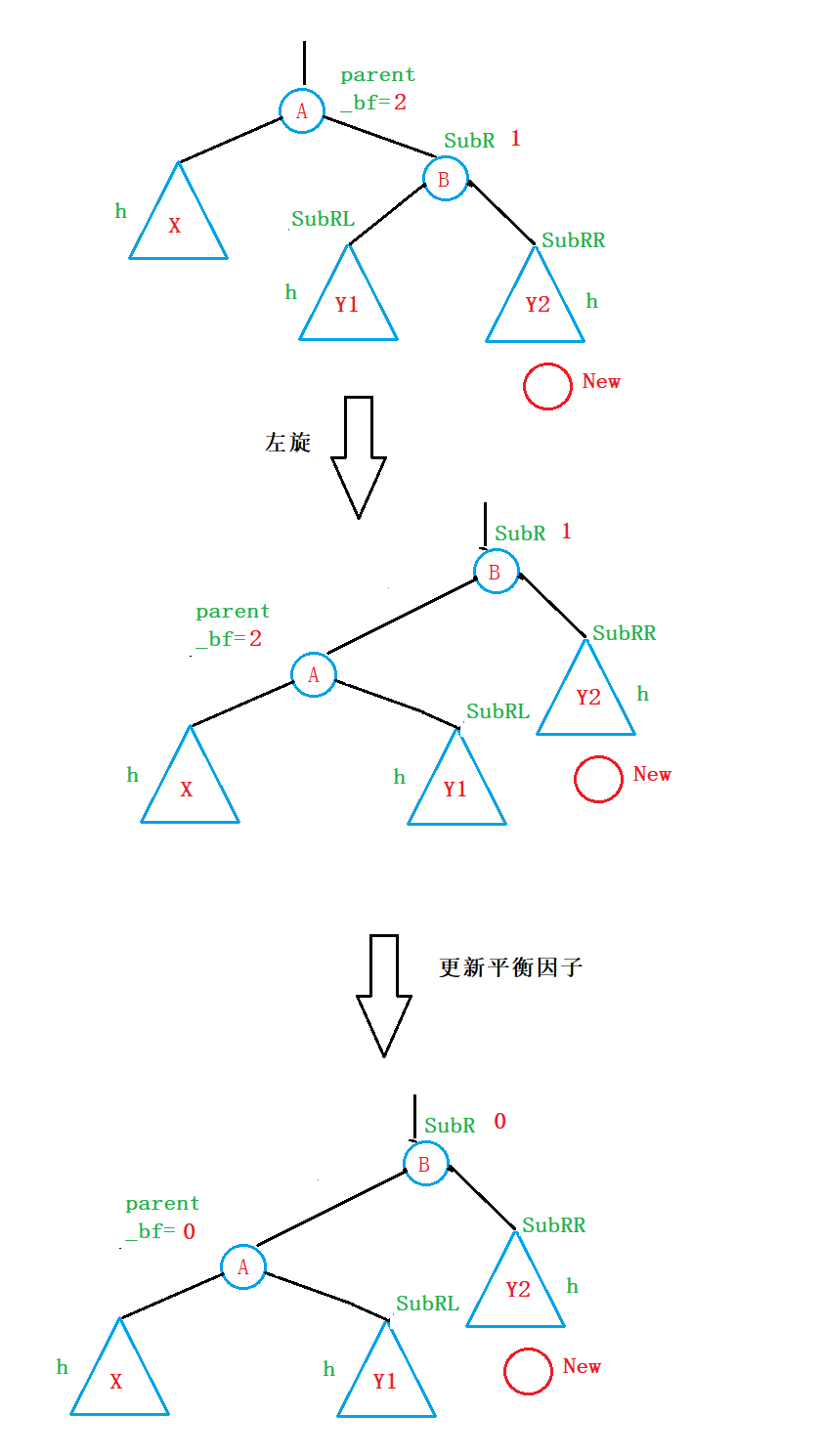
①假设插入的节点插入在Y2子树中(RR型)
这里解释一下为什么叫RR型:插入节点插在parent的右节点的右子树中；
第一个R表示parent的右节点，第二个R表示parent的右节点的右子树;
为了表示方便，我们将parent的右节点用SubR表示，右节点的右子树用SubRR来表示：
右节点的左子树用SubRL来表示：
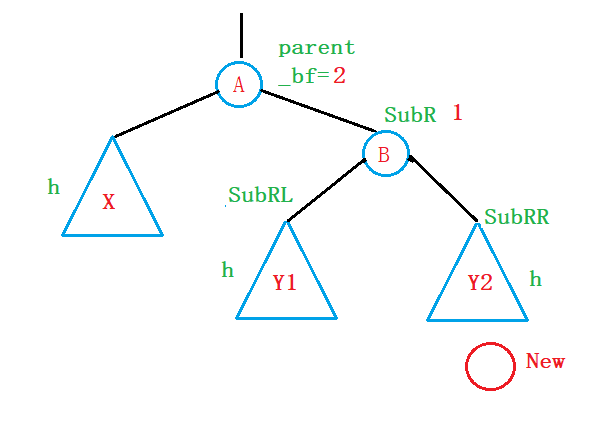
在这里插入图片描述

旋转方法：

让Y1子树作为parent节点的右子树;
让parent这课树作为SubR节点的左子树；
更新parent节点与SubR节点的平衡因子(都更新为0);
这种方法叫做左旋！
为什么这种旋转方法可行？
别忘了AVL树还是可二叉搜索树，Y1子树中的所有节点都是大于parent节点的吧！那么用Y1子树来充当parent的右子树，自然没问题啊，符合搜索二叉树的要求；好，现在parent这课树整体是小于SubR节点的吧！(parent1节点小于SubR节点，X子树也小于SubR节点，Y1子树也小于SubR节点)那么很自然的这种旋转方式是可行的：

通过检查旋转过后的平衡因子，我们发现，旋转过后所得到的子树是符合AVL树的条件的；

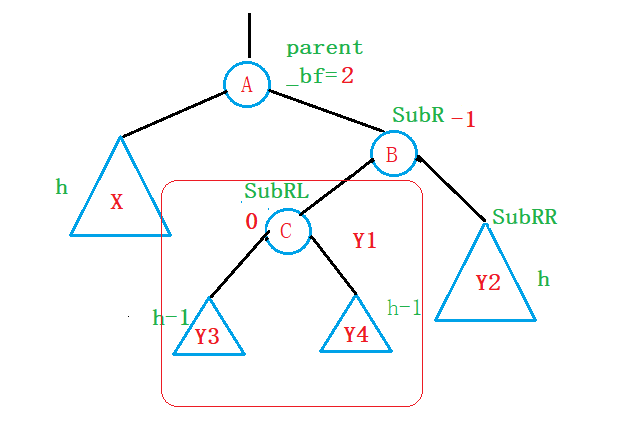
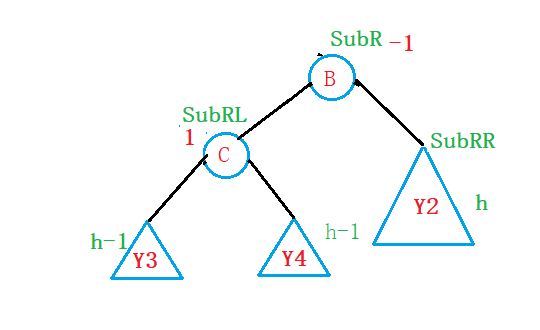
②假设插入的节点插入在Y1子树中(RL型)

这里解释一下为什么叫RL型:插入节点插在parent的右节点的左子树中；
第一个R表示parent的右节点，第二个L表示parent的右节点的左子树;
为了表示方便，我们将parent的右节点用SubR表示，右节点的右子树用SubRR来表示：
右节点的左子树用SubRL来表示：
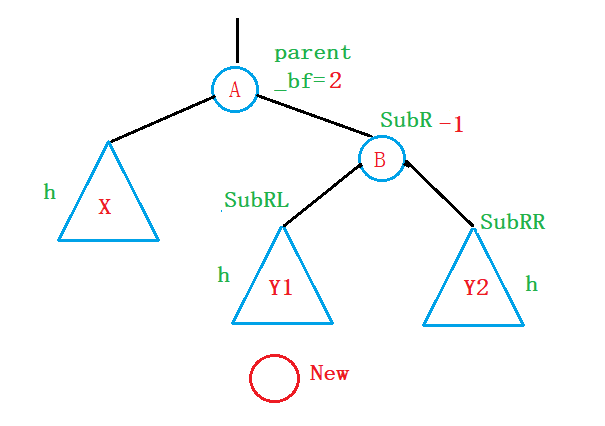
在这里插入图片描述

为此，对于这种情况，我们再次尝试利用左旋的方法来尝试一下：
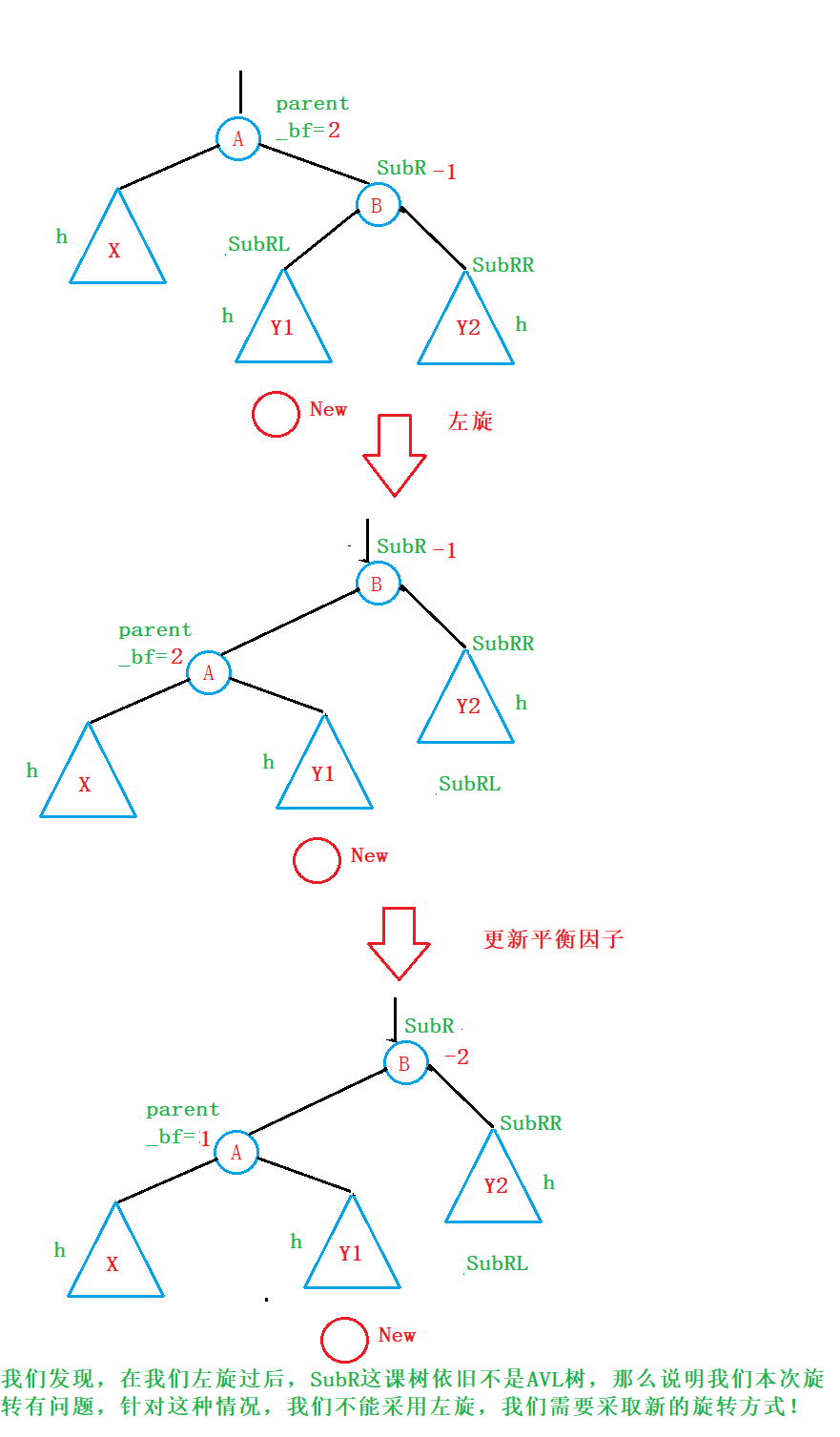
在这里插入图片描述
很显然，左旋的方法针对这种情况失效了，我们需要采取一种新的旋转方法；

旋转方法：
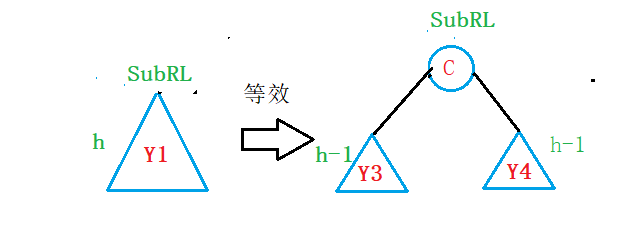
先将SubRL也就是Y1这颗树进行进行等效：

至此，我们替换一下原图：

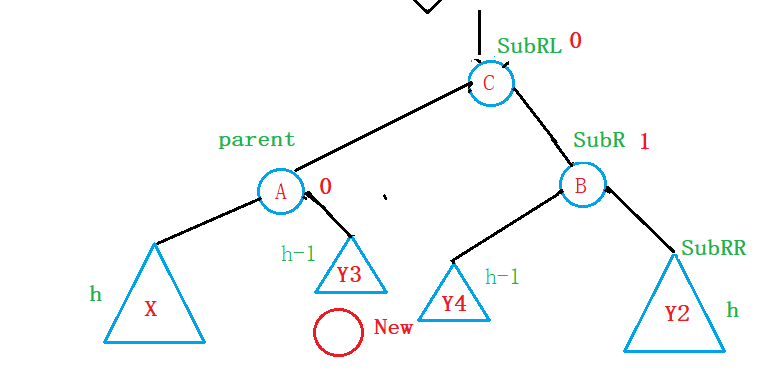
因此，我们的New节点既可以插在Y3子树中，也可以插在Y4子树中，无论插在那边旋转的方式是一样的，只是最后更新parent、SubR、SubRL这三个节点的平衡因子时有所差别；
这里我们就不分类讨论了；
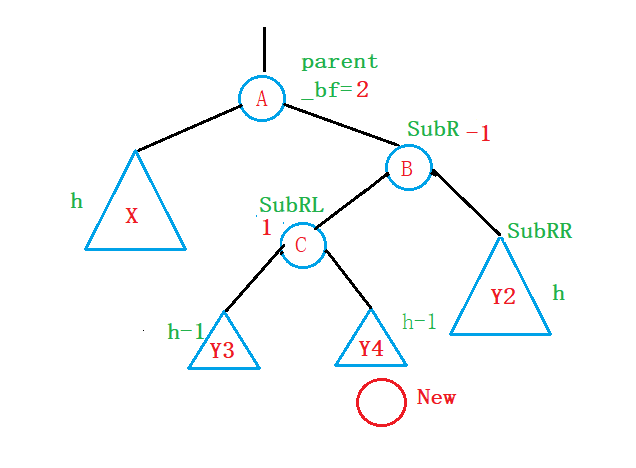
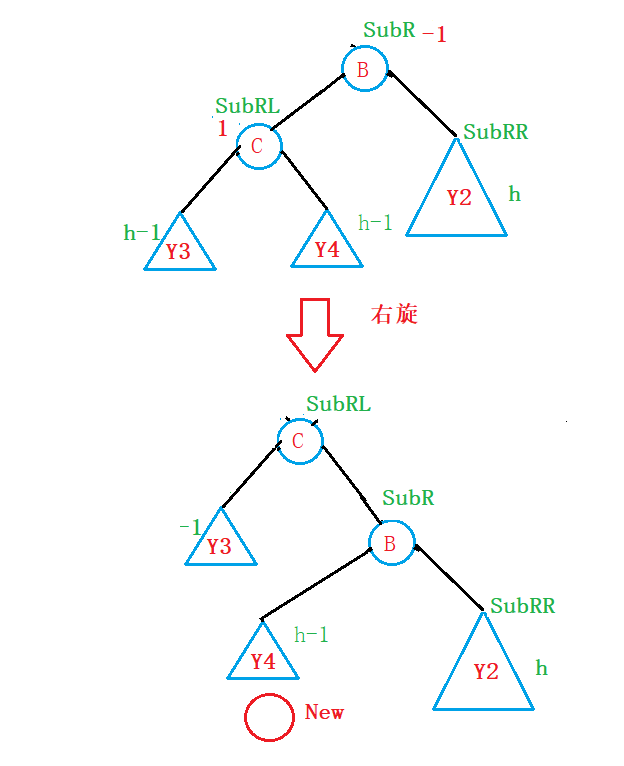
就先假设新节点就插入在Y4子树中：

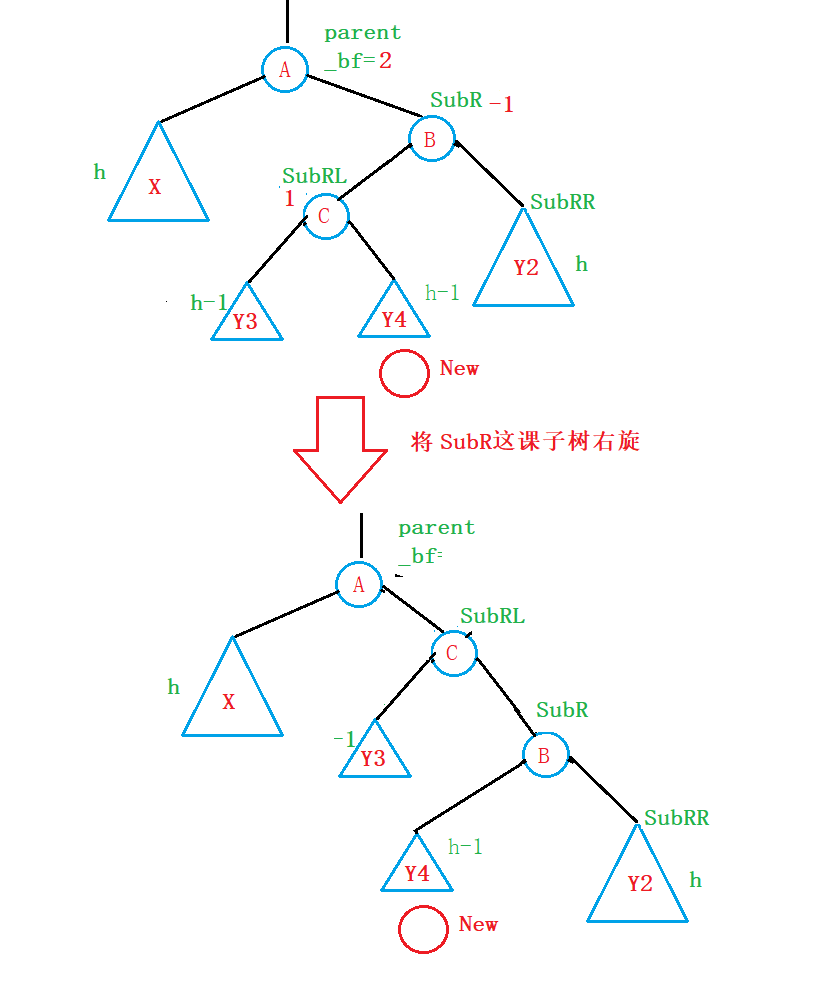
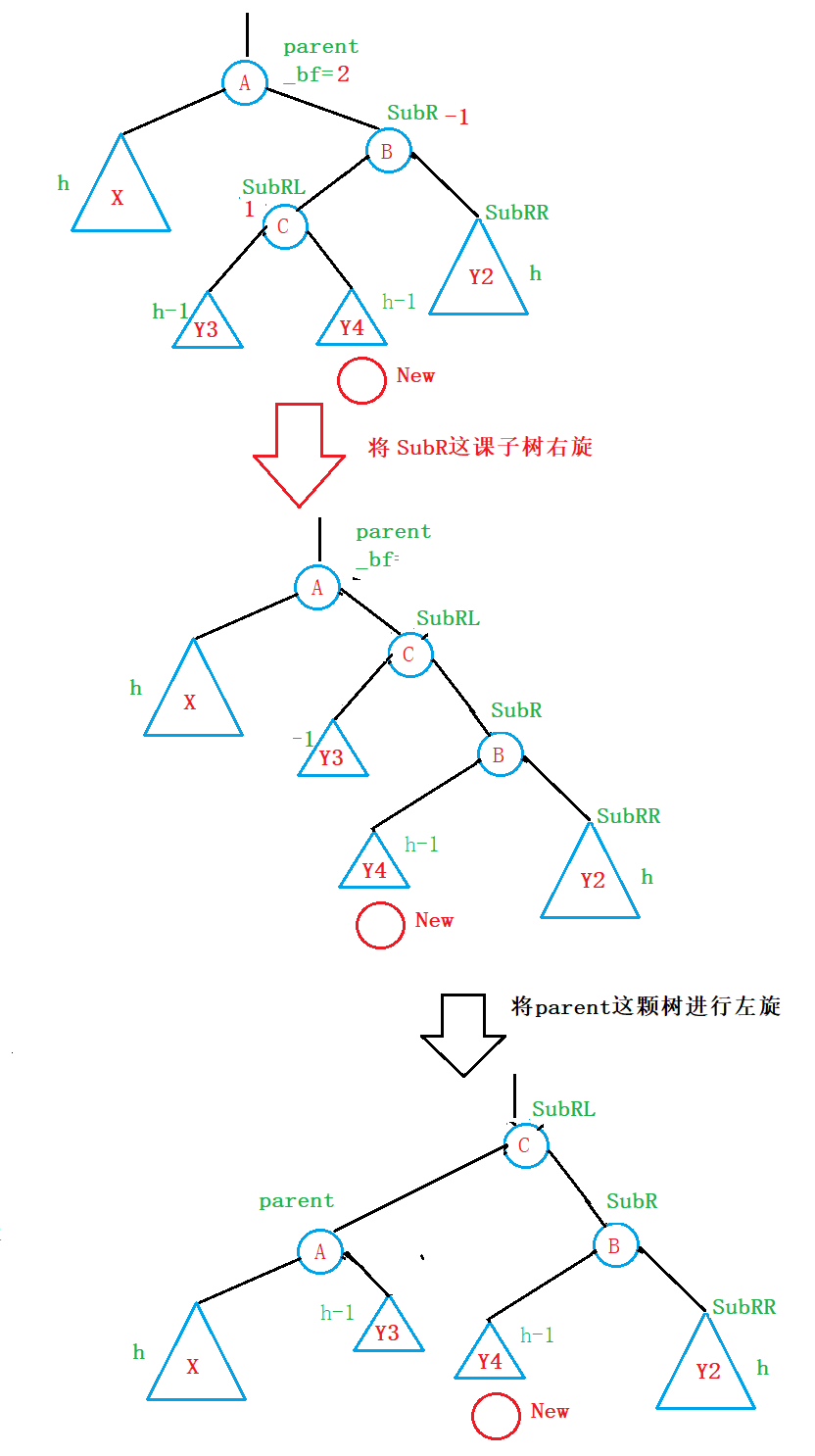
因此，我们给出的旋转方式是:

先将SubR这颗子树右旋：

何为右旋?
我们就以SubR这颗子树为例吧：

右旋：
a . Y4子树作为SubR节点的左子树；
b . 将SubR这课子树作为 SubRL节点的右子树;
c . 更新SubRL、SubR的平衡因子(都更新为0)；

为什么可行？
读者可以自行验证；
通过右旋SubR这颗树，我们可以很明显的看出来，parent这课树变成了右边高，左边低，因此，对于这种情况，我们对于parent这课树进行左旋：

更新平衡因子：
更新平衡因子可是个大事,
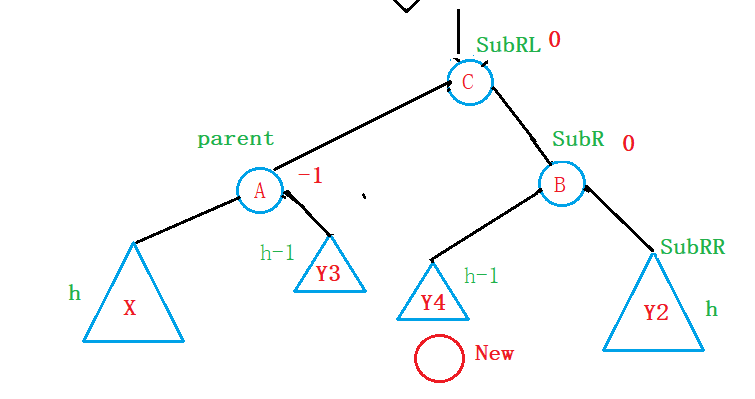
根据新节点插入的子树不同，更新的平衡因子也是不同:
若新节点插在Y4中，则平衡因子的更新为：

SubR->_bf=0;
parent->_bf=-1;
SubR->_bf=0;
若新节点插在Y3中，则平衡因子的更新为：

SubR->_bf=0;
parent->_bf=0;
SubR->_bf=1;
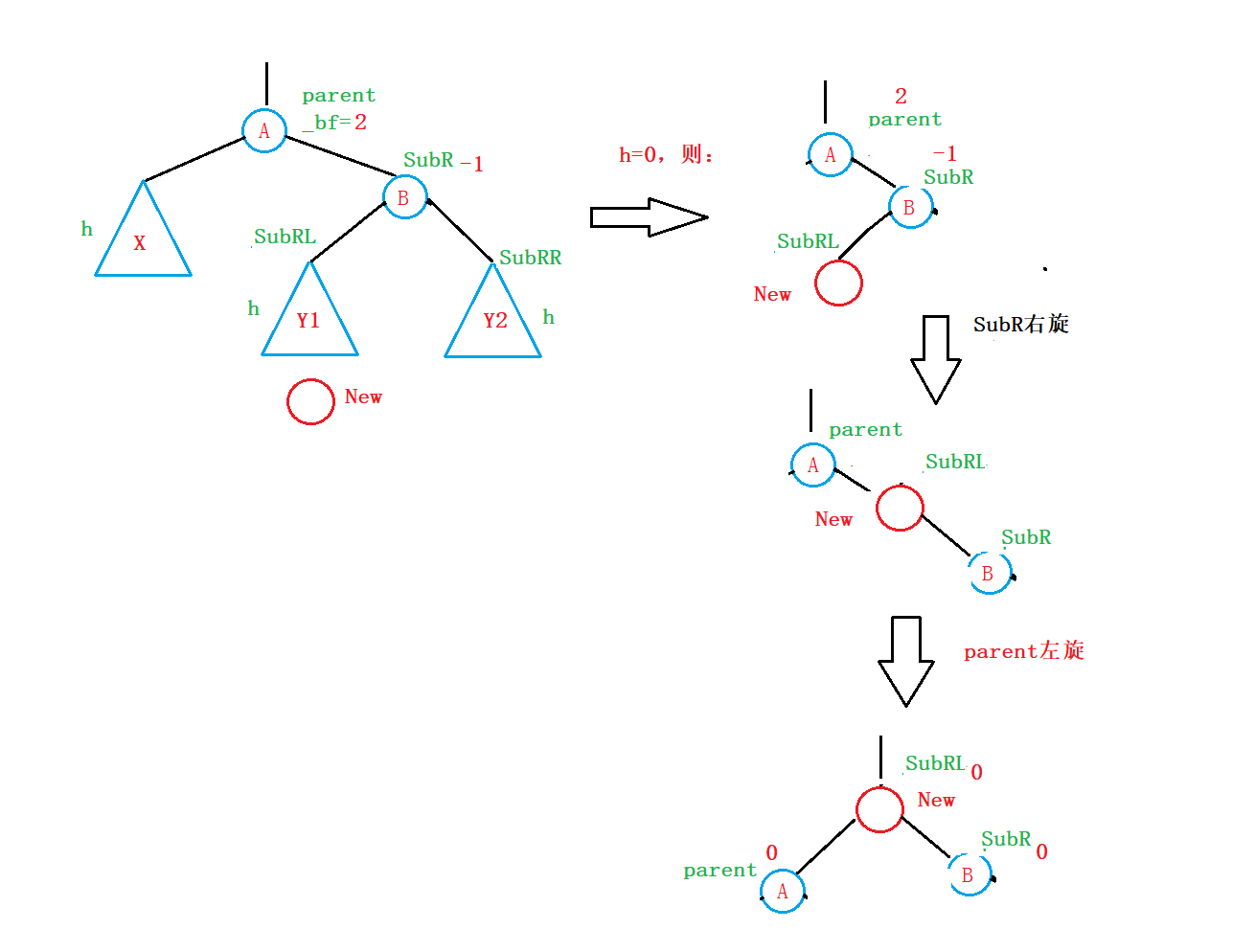
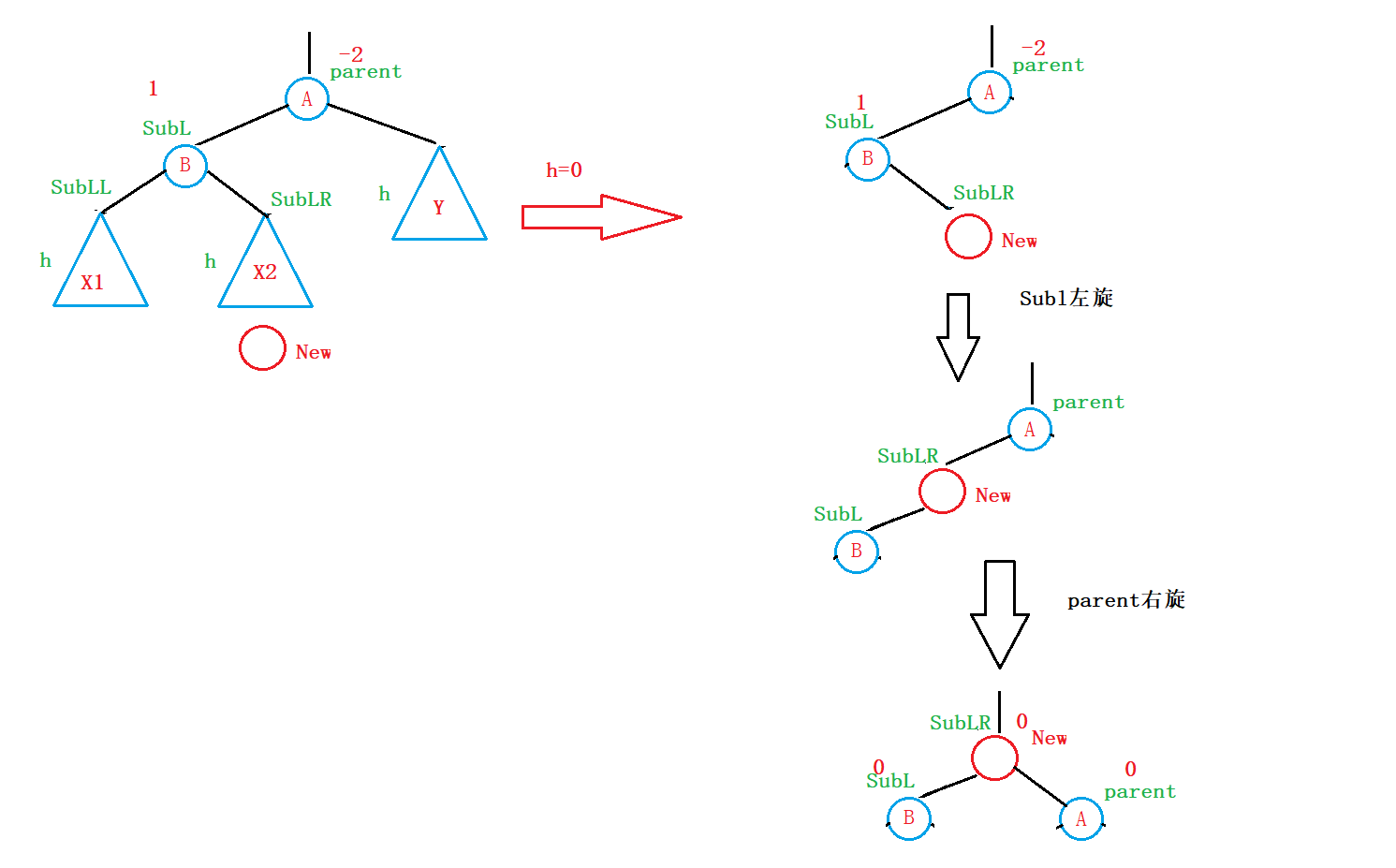
可是前面的插入，都是建立在Y3，Y4存在的情况，如果Y3、Y4子树不存在呢？
何为不存在？
正常情况下，h的取值是0、1、2、3、4、… 整数;
如果h=0,那么不就是Y3 ,Y4 不存在的情况嘛：
为此这时，我们的平衡因子更新为：

SubR->_bf=0;
parent->_bf=0;
SubR->_bf=0;
至此，我们完成了RL型的旋转以及平衡因子的更新！

二、假设插入节点过后，parent-> _bf == -2:

那么这种情况对应图二：
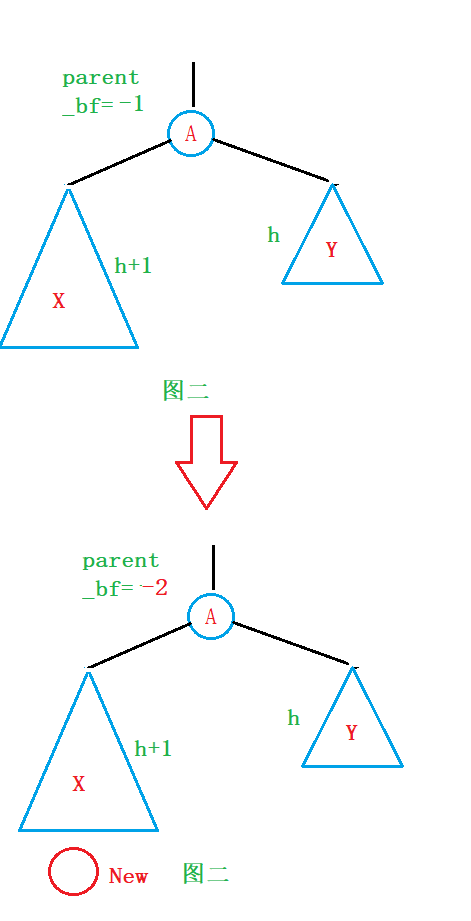
在这里插入图片描述

实际上parent-> _bf=-2这种情况，就是parent-> _bf =2 的对称变换，有了parent-> _bf=2这种情况的经验，我们再讨论这种情况时，就简单一点：

为了讨论的方便，我们可以做一个等效变换，我们将X树等效为：
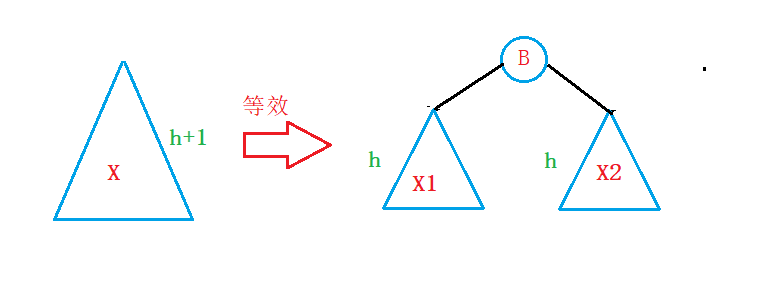
在这里插入图片描述
将其替换进图二：

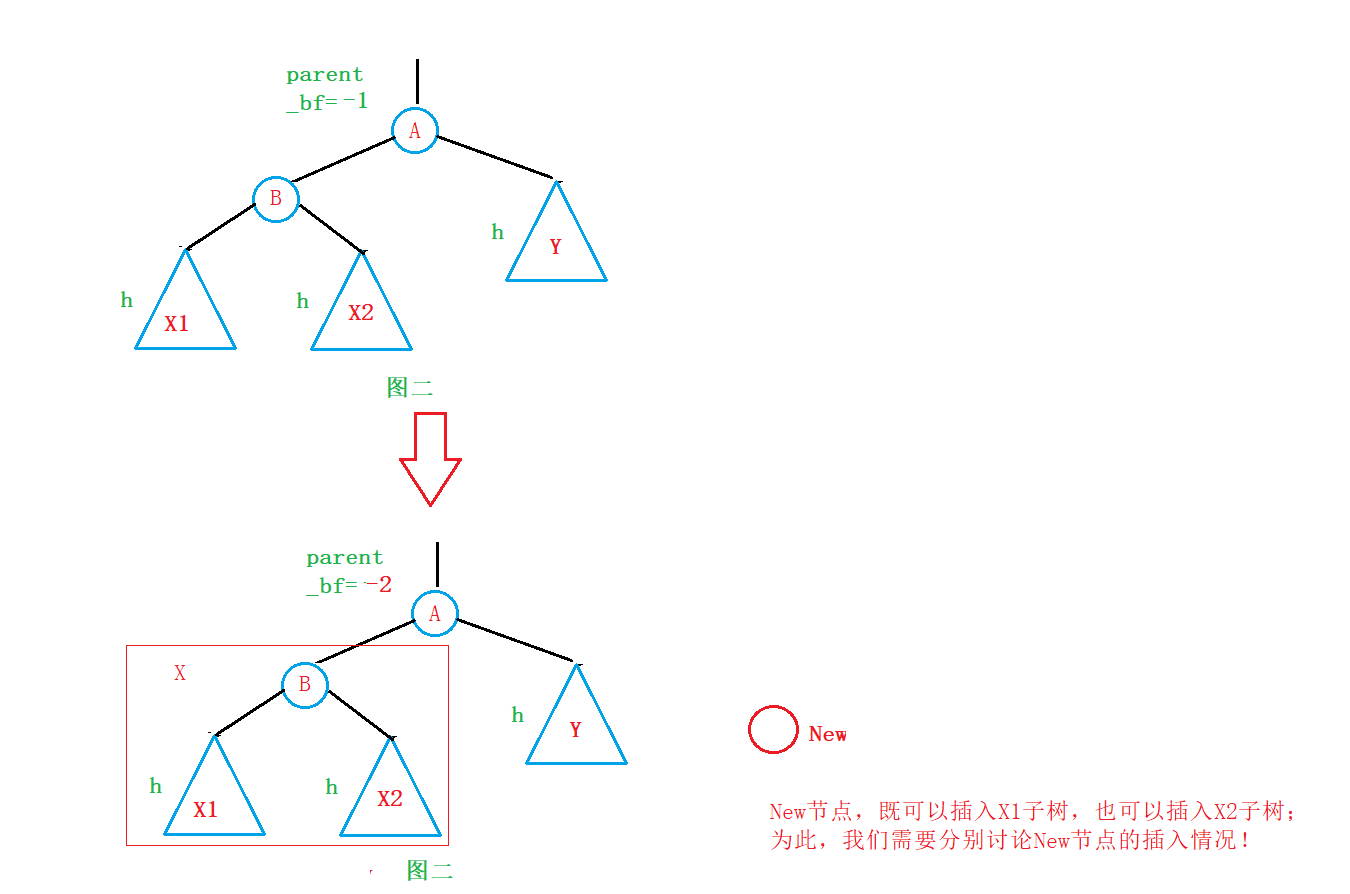
在这里插入图片描述

①假设插入的节点插入在Y1子树中(LL型)
这里解释一下为什么叫LL型:插入节点插在parent的左节点的左子树中；
第一个L表示parent的左节点，第二个L表示parent的左节点的左子树;
为了表示方便，我们将parent的左节点用SubL表示，左节点的右子树用SubLR来表示：
左节点的左子树用SubLL来表示：
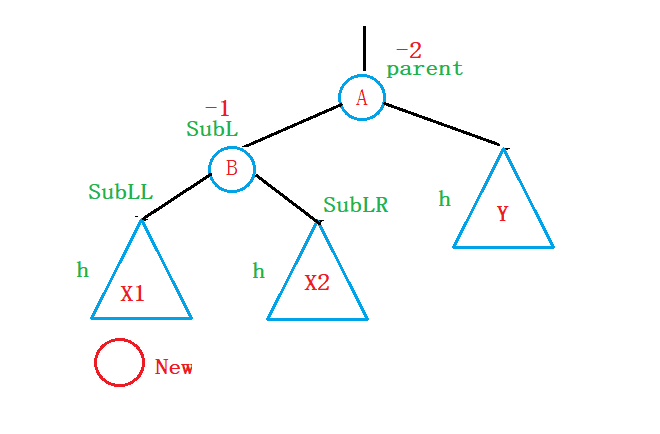
在这里插入图片描述

旋转方法：

将X2子树作为parent的右子树；
将parent这颗子树作为SubL节点的右子树；
更新parent节点、SubL节点的平衡因子(都是0)；
这种方法叫做右旋！
为什么这种旋转方法可行？
首先，根据搜索二叉树的性质，X2这课子树是小于parent这个节点的，那么X2可以作为parent这个节点的左子树对吧！然后呢，parent这颗子树又是大于于SubL这个节点的对吧!(parent节点大于SubL节点、SubLR子树大于于SubL节点、Y子树大于SuL节点)；这也就是为什么这种旋转方式行的原因；

通过检查旋转过后的平衡因子，我们发现，旋转过后所得到的子树是符合AVL树的条件的；

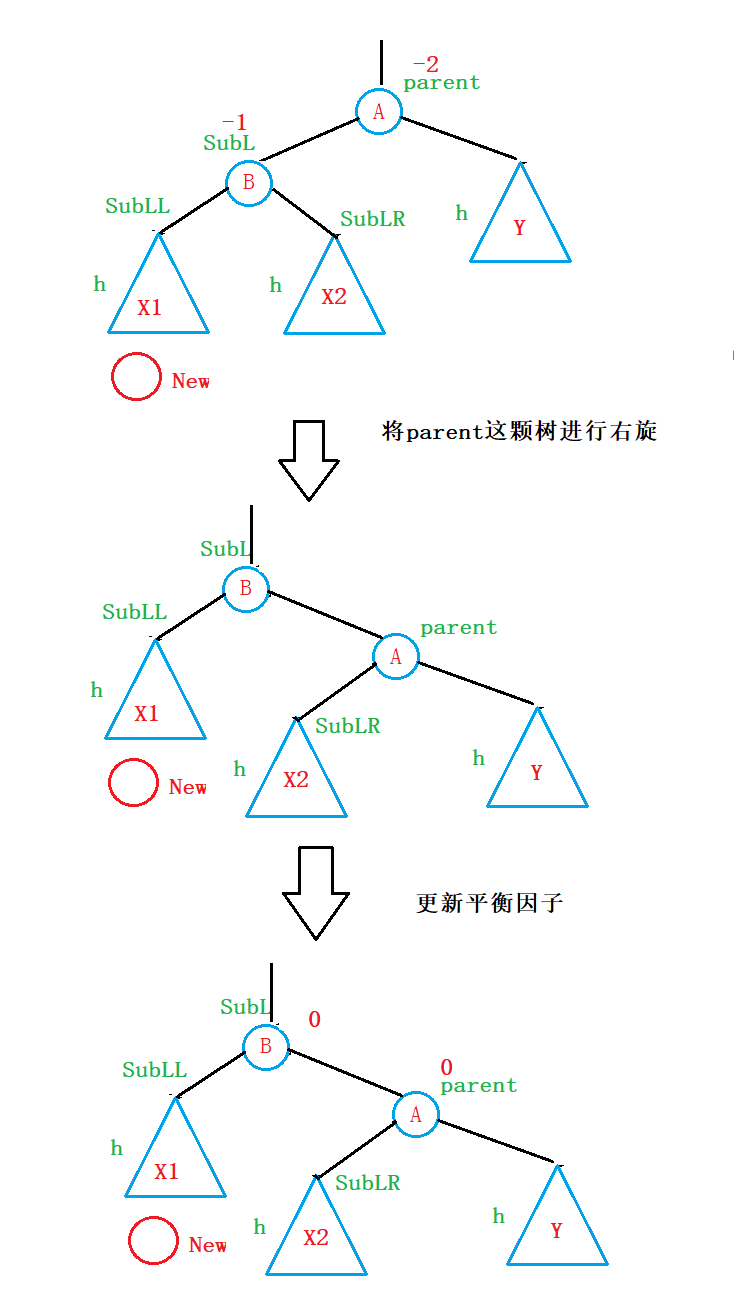
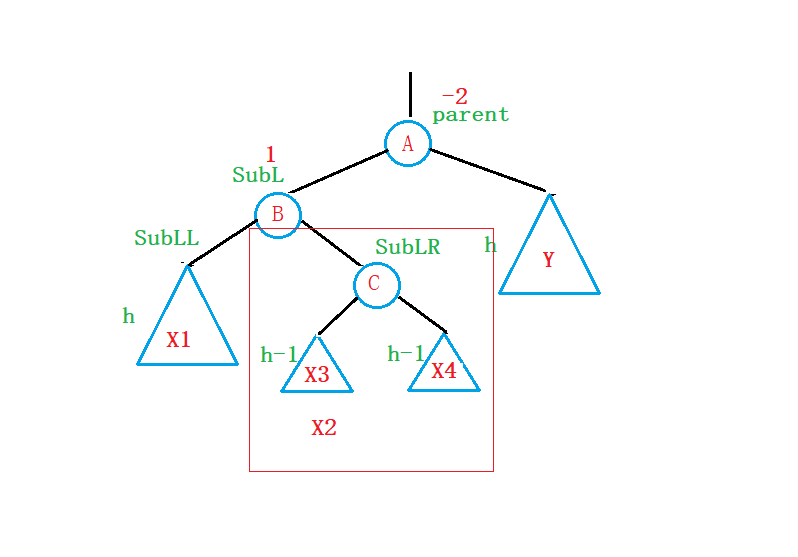
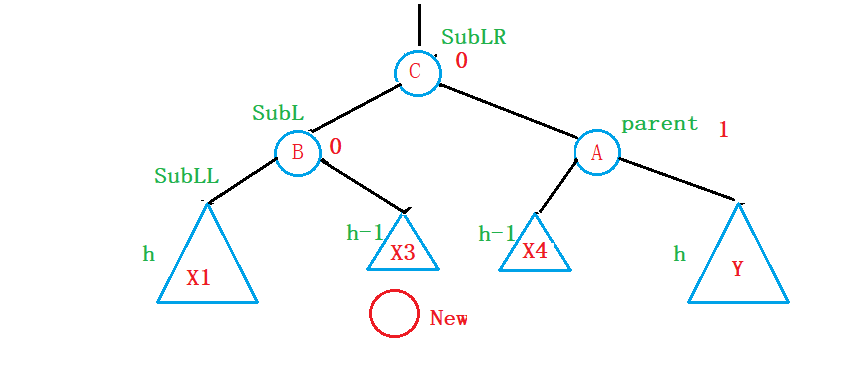
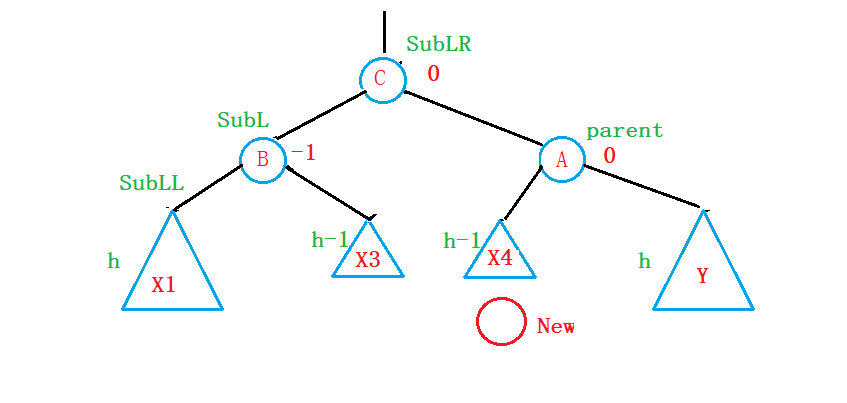
②假设插入的节点插入在X2子树中(LR型)

这里解释一下为什么叫LR型:插入节点插在parent的左节点的右子树中；
第一个L表示parent的左节点，第二个R表示parent的左节点的右子树;
为了表示方便，我们将parent的左节点用SubL表示，左节点的右子树用SubLR来表示：
左节点的左子树用SubLL来表示：
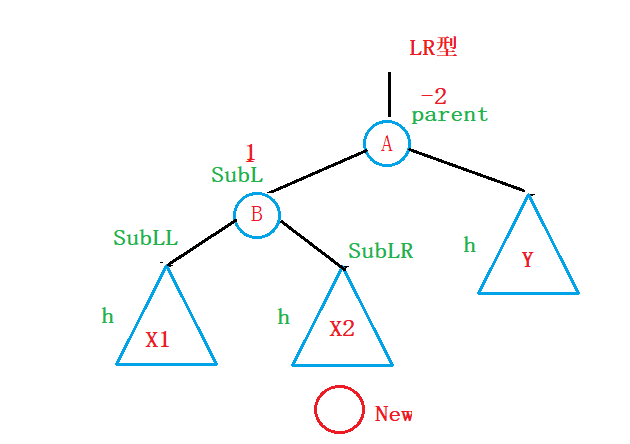
在这里插入图片描述

为此，对于这种情况，我们再次尝试利用右旋的方法来尝试一下：
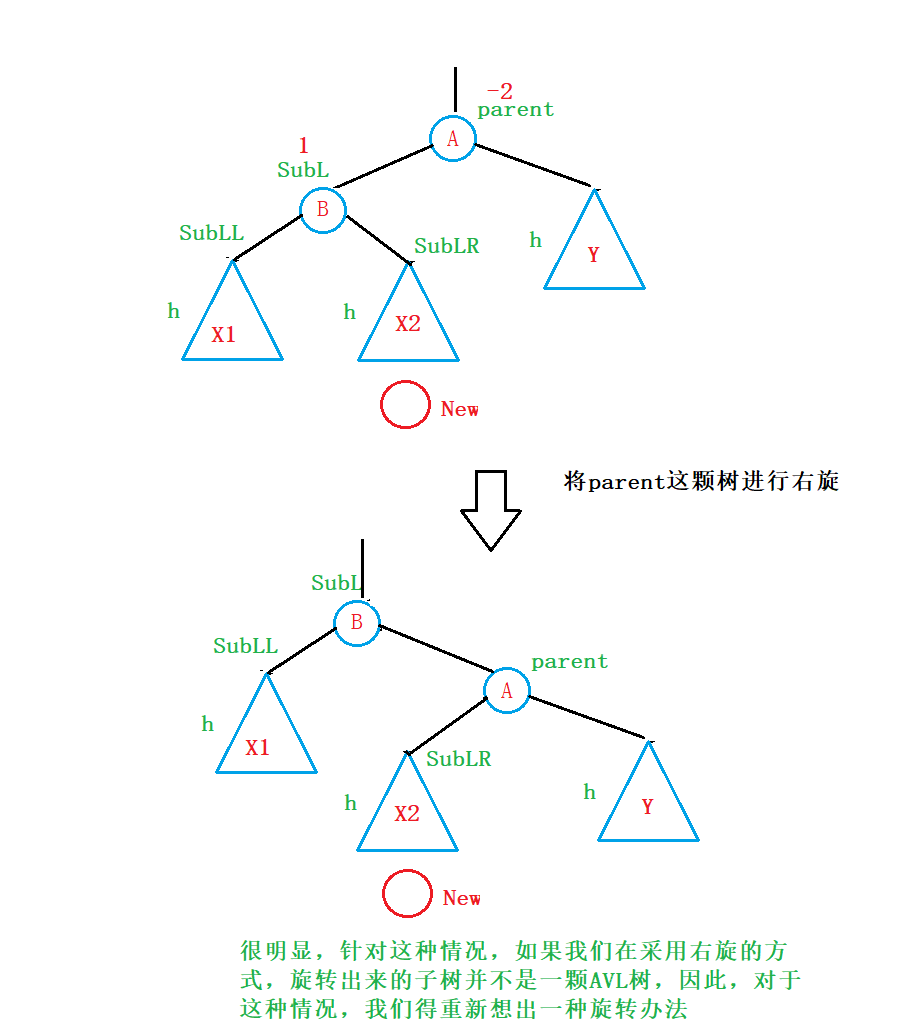
在这里插入图片描述

旋转办法：
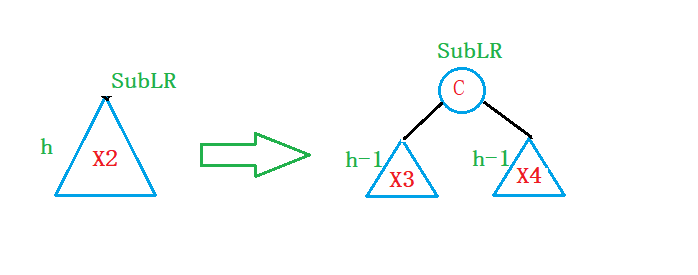
为了方便问题的解决，我们将X2进行一下等效：

至此，我们替换一下原图：

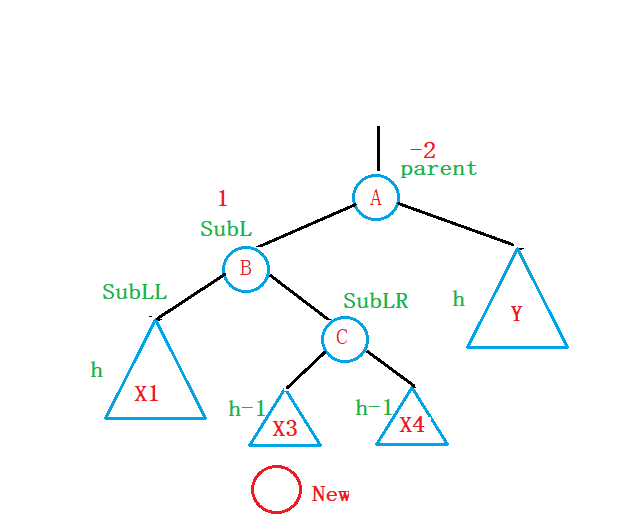
因此，我们的New节点既可以插在X3子树中，也可以插在X4子树中，无论插在那边旋转的方式是一样的，只是最后更新parent、SubR、SubRL这三个节点的平衡因子时有所差别；
这里我们就不分类讨论了；
就先假设新节点就插入在X3子树中：

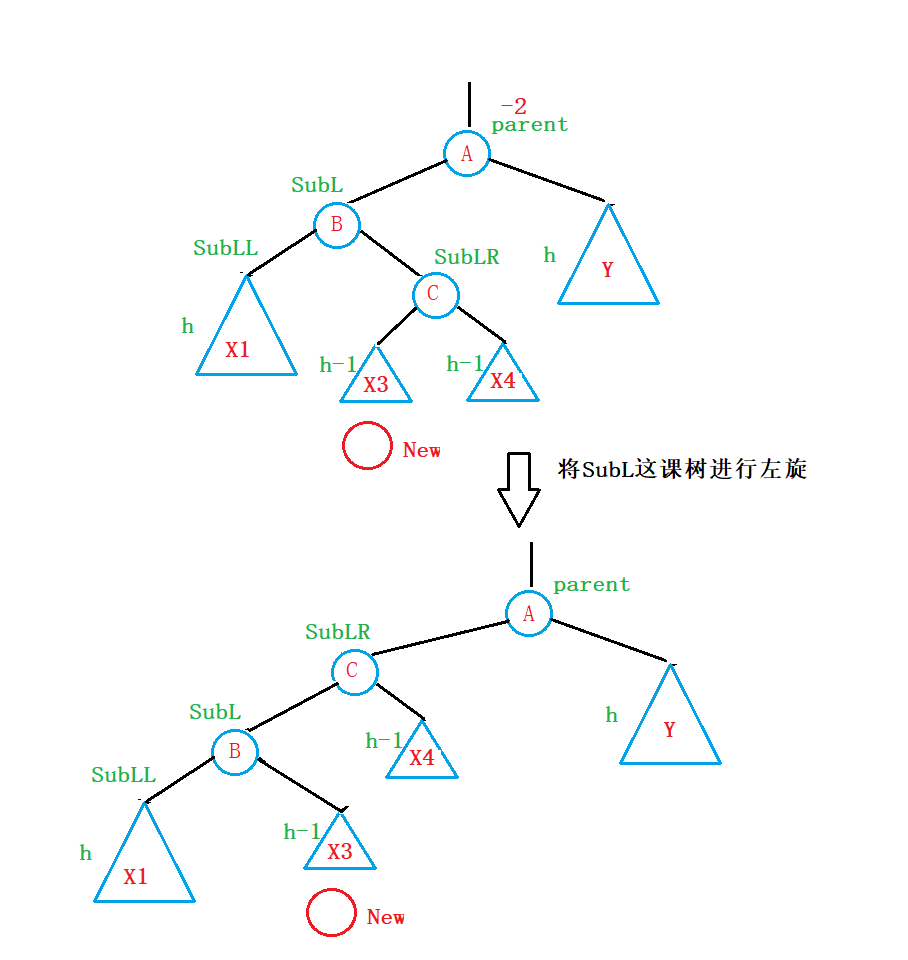
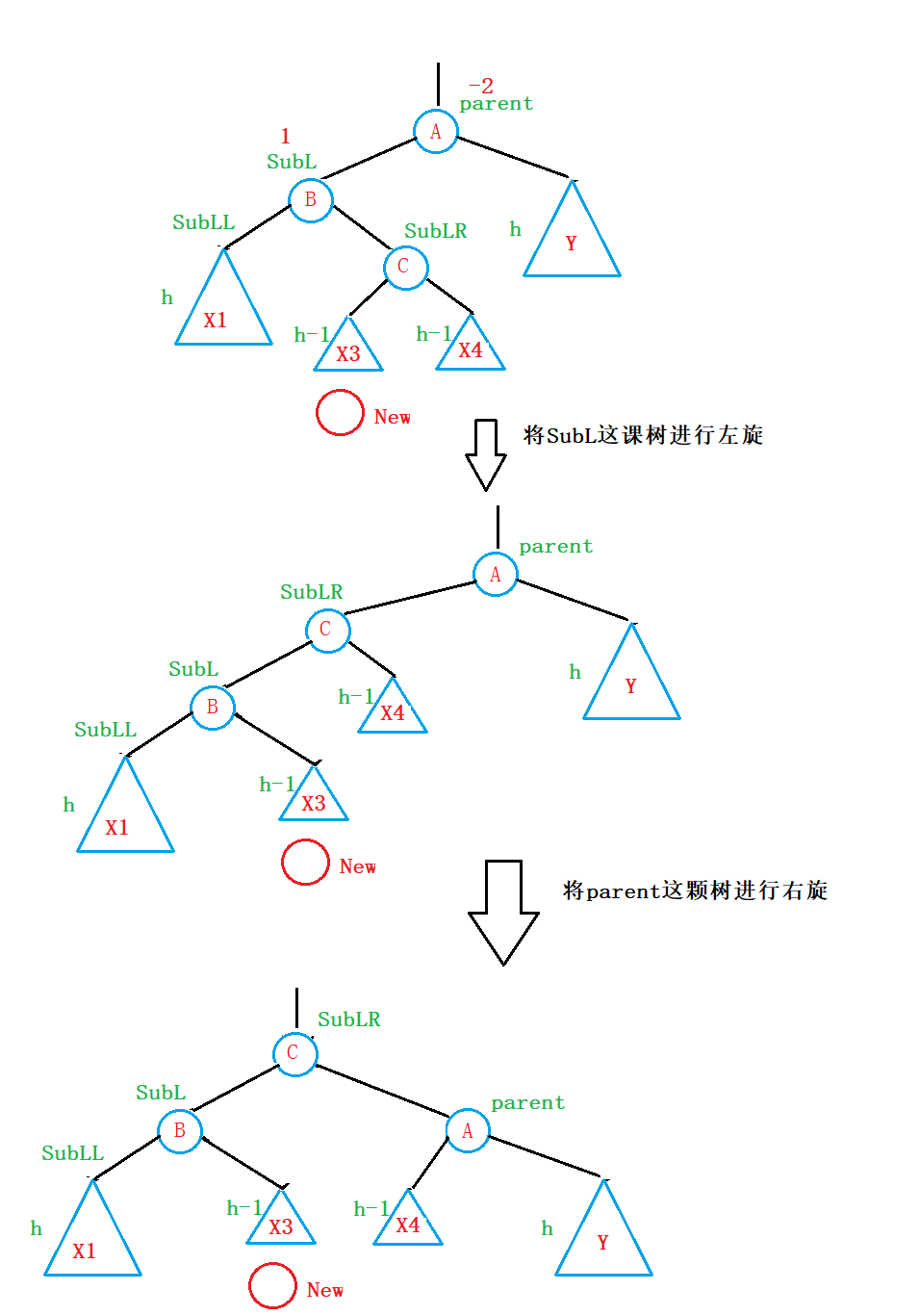
因此，我们给出的旋转方式是:

将SuL这颗树进行左旋：

将parent这颗树进行右旋：

3.更新平衡因子：
更新平衡因子可是个大事,
根据新节点插入的子树不同，更新的平衡因子也是不同:
若新节点插在X3中，则平衡因子的更新为：

SubLR->_bf=0;
parent->_bf=1;
SubL->_bf=0;
若新节点插在X4中，则平衡因子的更新为：

SubLR->_bf=0;
parent->_bf=0;
SubL->_bf=-1;
可是前面的插入，都是建立在X3，X4存在的情况，如果X3、X4子树不存在(X3、X4是空树也算存在)呢？
何为不存在？
正常情况下，h的取值是0、1、2、3、4、… 整数;
如果h=0,那么不就是X3 ,X4 不存在的情况嘛：
为此这时，我们的平衡因子更新为：

SubLR->_bf=0;
parent->_bf=0;
SubL->_bf=0;
至此，我们完成了LR型的旋转以及平衡因子的更新！

至此整个AVL树的插入的旋转就算是完成了；
如果，你能坚持看到这里，并对AVL树的旋转有了清晰的认识了，那我觉得这件事:
在这里插入图片描述

AVL树的插入操作的代码

bool insert(const std::pair<K, V>& data)
{
	Node* parent = nullptr;
	Node* cur = _root;
	if (_root == nullptr)//空树
	{
		_root = new Node(data);
		return true;
	}
	while (cur)
	{
		parent = cur;
		if (cur->_data.first == data.first)
			return false;
		else if (cur->_data.first > data.first)
			cur = cur->_left;
		else
			cur = cur->_right;
	}
	cur = new Node(data);
	cur->_parent = parent;//记住要维护父指针域
	if (parent->_data.first > cur->_data.first)
		parent->_left = cur;
	else
		parent->_right = cur;
	//插入一个节点过后，必定导致，cur这个节点的祖宗节点的平衡因子改变，我们需要跟新cur的父节点的平衡因子
	while (parent)
	{
	//cur是parent的右孩子,parent右孩子_bf++
		if (cur->_data.first > parent->_data.first)
			parent->_bf++;
		else
			parent->_bf--;
		//检查更新过后的parent的平衡因子，然后做出不同的反应
		if (parent->_bf == 0)
		{
			//更新过后parent的平衡因子为0，那么更新之前parent的平衡因子一定是 ±1 （可列方阵=程验证）;
			//这说明，新插入的节点，是插在parent矮的一颗子树上的，parent这棵树的高度不变，无需在更新祖宗节点的平衡因子;
			//此次插入，非常成功
			break;
		}
		else if (abs(parent->_bf) == 1)
		{
			//更新过后parent的平衡因子是 ±1 那么说明更新之前parent的_bf一定是0
			//这说明在此次插入过后，parent这棵树的高度增加了，必须更新祖宗节点的_bf
			parent = parent->_parent;//parent、cur直接往上更新
		}
		else if (abs(parent->_bf) == 2)
		{
			//更新过后parent的平衡因子是 ±2 ,那么说明更新之前parent的_bf一定是±1；
			//这说明，此时parent这课树已经失衡了，需要旋转parent这课树
			//不平衡又有四种情况，这四种情况，对应不同的旋转方法

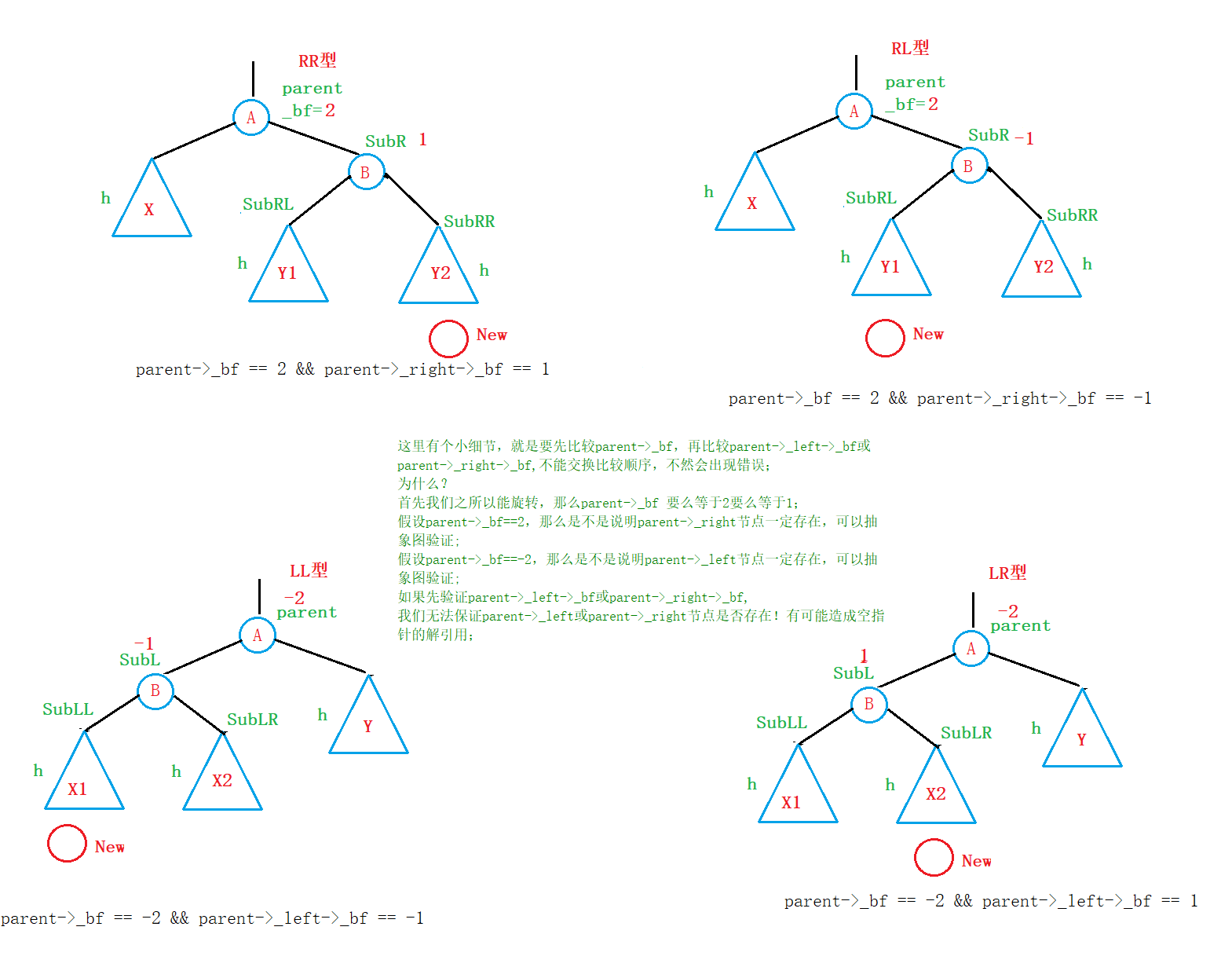
			//这里有个小细节，就是要先比较parent->_bf，再比较parent->_left/parent->_right,不能交换比较顺序，不然会出现错误
			if (parent->_bf == 2 && parent->_right->_bf == 1)//（RR型）
			{
				//parent左旋
				RotateL(parent);
			}
			else if (parent->_bf == -2 && parent->_left->_bf == -1)//(LL型)
			{
				//parent右旋
				RotateR(parent);
			}
			else if (parent->_bf == 2 && parent->_right->_bf == -1)//(RL型)
			{
				//先记录一下parent的右节点的左节点的_bf
				Node* SubR = parent->_right;
				Node* SubRL = SubR->_left;//放心这个节点一定存在，可证明
				int bf = SubRL->_bf;
				//1、先parent->_right右旋
				RotateR(parent->_right);
				//2、再parent左旋
				RotateL(parent);
				//这里我们需要重新更新一下平衡因子，因为单单的左旋、右旋只会将平衡因子置0，这是不正确的，需要我们手动调节
				if (bf == -1)
				{
					SubRL->_bf = 0;
					parent->_bf = 0;
					SubR->_bf = 1;
				}
				else if (bf == 1)
				{
					SubRL->_bf = 0;
					SubR->_bf = 0;
					parent->_bf = -1;
				}
				else if (bf == 0)
				{
					SubRL ->_bf= 0;
					SubR ->_bf= 0;
					parent->_bf = 0;
				}
				else
				{
					assert(false);
				}
			}
			else if (parent->_bf == -2 && parent->_left->_bf == 1)//(LR型)
			{
				Node* SubL = parent->_left;
				Node* SubLR = SubL->_right;//放心这个节点一定存在，可证明
				int bf = SubLR->_bf;
				//1、先parent->_left左旋
				RotateL(parent->_left);
				//2、再parent右旋
				RotateR(parent);
				//平衡因子调节
				if (bf == -1)
				{
					SubLR->_bf = 0;
					SubL->_bf = 0;
					parent->_bf = 1;
				}
				else if (bf == 1)
				{
					SubLR->_bf = 0;
					SubL->_bf = -1;
					parent->_bf = 0;
				}
				else if (bf == 0)
				{
					SubLR->_bf = 0;
					SubL->_bf = 0;
					parent->_bf = 0;
				}
				else
				{
					assert(false);
				}
			}
			else
			{
			//不用说了，插入之前的AVL树就已经出问题了
				assert(false);
			}
			//无论哪种旋转，旋转完毕过后，头结点平衡因子都为0了，
			//这课树已经平衡了，不需要在向上调整了
			break;
		}
		else
		{
//如果更新完过后parent->_bf等于1、-1、0、-2、2之外的数，不用说了，插入之前的AVL树就已经出问题了
     	assert(false);
		}
	}
	return true;
}
void RotateR(Node* parent)
{
	Node* SubL = parent->_left;
	Node* SubLR = SubL->_right;
	Node* ppNode = parent->_parent;

	parent->_left = SubLR;
	if (SubLR)//SubLR节点存在
		SubLR->_parent = parent;

	SubL->_right = parent;
	parent->_parent = SubL;
	if (ppNode == nullptr)//parent是根节点
	{
		SubL->_parent = nullptr;
		_root = SubL;
	}
	else
	{
		SubL->_parent = ppNode;
		if (ppNode->_data.first > SubL->_data.first)
			ppNode->_left = SubL;
		else
			ppNode->_right = SubL;
	}
	SubL->_bf = 0;
	parent->_bf = 0;
}
void RotateL(Node* parent)
{
	Node* SubR = parent->_right;//这个节点一定存在，可以证明
	Node* SubRL = parent->_right->_left;//这个节点就不一定存在了
	Node* ppNode = parent->_parent;//提前记录一下parent的父亲
	//开始链接SubRL节点
	parent->_right = SubRL;
	if (SubRL)//只有当这个节点存在时，才需要维护器=其父亲节点
		SubRL->_parent = parent;
	//开始链接parent节点
	SubR->_left = parent;
	parent->_parent = SubR;

	//开始链接SubR节点
	if (ppNode == nullptr)//如果parent就是根，那么需要更新根节点
	{
		SubR->_parent = nullptr;
		_root = SubR;
	}
	else//parent不是根节点
	{
		SubR->_parent = ppNode;
		if (ppNode->_data.first > SubR->_data.first)
			ppNode->_left = SubR;
		else
			ppNode->_right = SubR;
	}
	//更新平衡因子
	SubR->_bf = 0;
	parent->_bf = 0;
}

代码中的细节

在这里插入图片描述

AVL树的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这
样可以保证查询时高效的时间复杂度，即 $log_2 (N)$ 。但是如果要对AVL树做一些结构修改的操
作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，
有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数
据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。