0. 基本介绍

SmoothL1Loss是一种常用的损失函数，通常用于回归任务中，其相对于均方差(MSE)损失函数的优势在于对异常值(如过大或过小的离群点)的惩罚更小，从而使模型更加健壮。

SmoothL1Loss的公式为：

$loss(x,y)=\{\begin{array}{ll}0.5(x-y{)}^2& \text{if }|x-y|<1\\ |x-y|-0.5& \text{otherwise}\end{array}$

其中，x和y分别为模型的输出和标签，|x-y|表示它们之间的差异。当|x-y|小于1时，采用平方误差；否则采用线性误差。这使得SmoothL1Loss相比于MSE更加鲁棒，即对于异常值的响应更加平缓。

在PyTorch中，可以使用nn.SmoothL1Loss()函数来构建SmoothL1Loss损失函数。

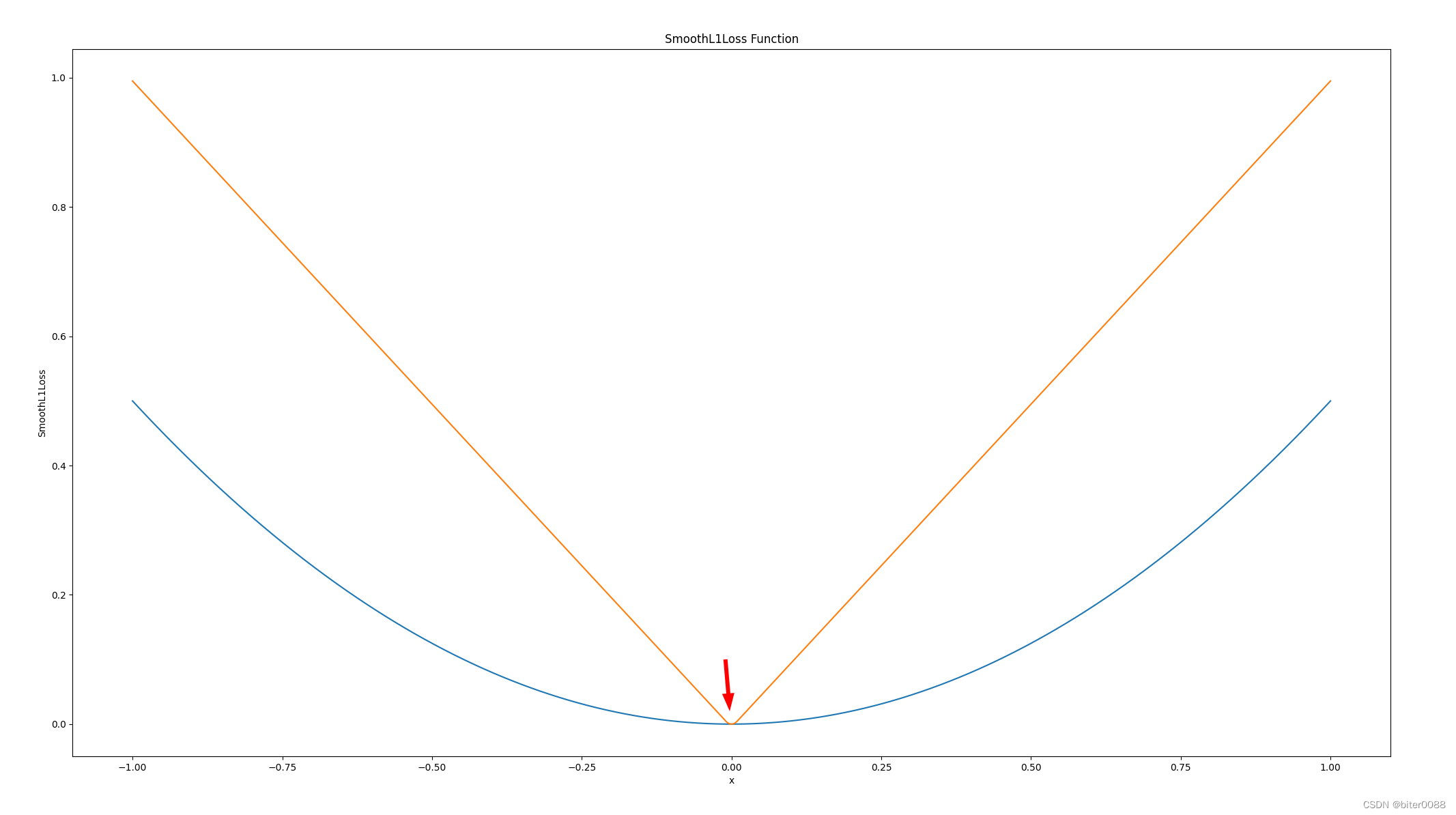
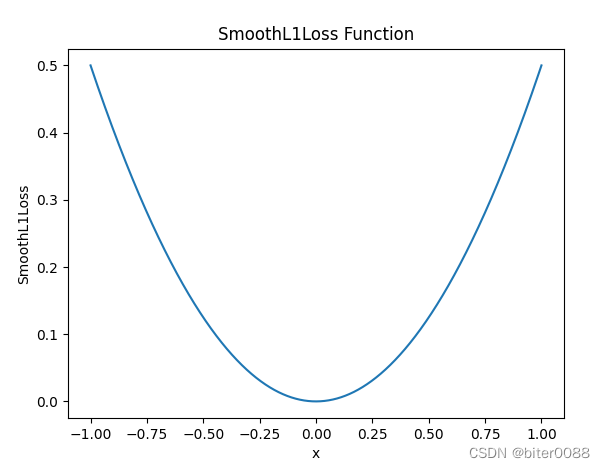
1. 绘制SmoothL1Loss函数

通过修改torch.linspace中的参数，可以改变图像的横坐标范围；通过修改torch.zeros中的参数，可以改变图像的高度和形状。

import torch.nn as nn
import matplotlib.pyplot as plt
import torch

# 定义函数和参数
smooth_l1_loss = nn.SmoothL1Loss(reduction='none')
x = torch.linspace(-1, 1, 10000)
y = smooth_l1_loss(torch.zeros(10000), x)

# x2 = 1e3*x
# y2 = 1e-3*smooth_l1_loss(torch.zeros(10000), x2)

# 绘制图像
plt.plot(x, y)
# plt.plot(x, y2)
plt.xlabel('x')
plt.ylabel('SmoothL1Loss')
plt.title('SmoothL1Loss Function')
plt.show()

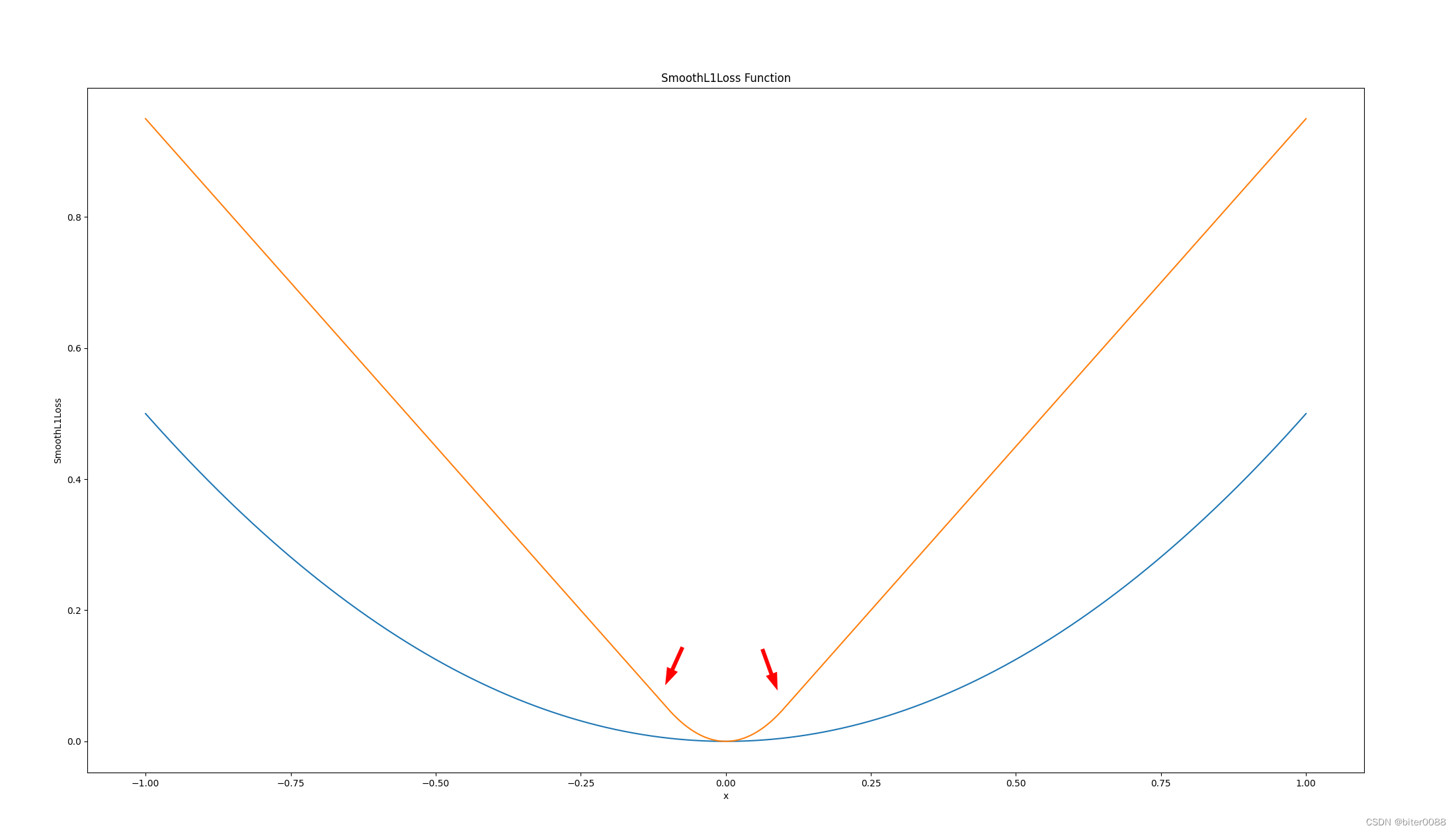
2. 移动SmoothL1Loss公式的临界点

移动临界点是为了在不尽兴其他操作的情况下，放大模型的损失

移动到0.1

import torch.nn as nn
import matplotlib.pyplot as plt
import torch

# 定义函数和参数
smooth_l1_loss = nn.SmoothL1Loss(reduction='none')
x = torch.linspace(-1, 1, 10000)
y = smooth_l1_loss(torch.zeros(10000), x)

x2 = 1e1*x
y2 = 1e-1*smooth_l1_loss(torch.zeros(10000), x2)

# 绘制图像
plt.plot(x, y)
plt.plot(x, y2)
plt.xlabel('x')
plt.ylabel('SmoothL1Loss')
plt.title('SmoothL1Loss Function')
plt.show()

如下，箭头处保持玩弯曲

移动到0.01

如下，箭头处还可以看到弯曲

import torch.nn as nn
import matplotlib.pyplot as plt
import torch

# 定义函数和参数
smooth_l1_loss = nn.SmoothL1Loss(reduction='none')
x = torch.linspace(-1, 1, 10000)
y = smooth_l1_loss(torch.zeros(10000), x)

x2 = 1e2*x
y2 = 1e-2*smooth_l1_loss(torch.zeros(10000), x2)

# 绘制图像
plt.plot(x, y)
plt.plot(x, y2)
plt.xlabel('x')
plt.ylabel('SmoothL1Loss')
plt.title('SmoothL1Loss Function')
plt.show()