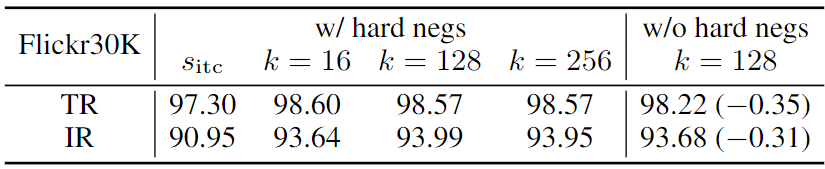堆栈
有人给出了堆栈用数组实现的另一种方式,即直接在函数参数中传递数组和top变量(而不是两者组成的结构指针),其中Push操作函数设计如下。这个Push函数正确吗?为什么?
#define MaxSize 100
ElementType S[MaxSize];
int top;
void Push(ElementType *S, int top, ElementType item)
{ if (top==MaxSize-1) {
printf(“堆栈满”); return;
}else {
S[++top] = item;
return;
}
}
分析:
问题出在函数参数的设计上。在函数定义中,数组S和变量top被作为参数传递。这意味着函数使用的是参数中的本地副本而不是全局变量。因此,Push函数实际上并没有改变全局变量top的值,也没有将新元素添加到堆栈中。
队列:
现采用大小为10的数组实现一个循环队列。设在某一时刻,队列为空且此时front和rear值均为5。经过若干操作后,front为8,rear为2,问:此时队列中有多少个元素?答案是4
分析:
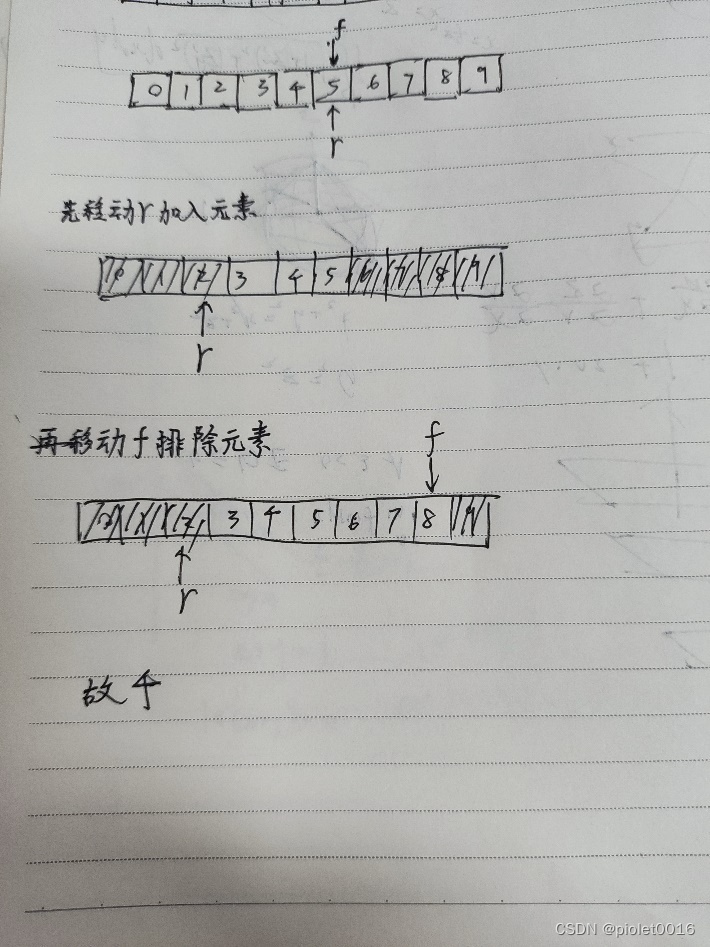
二叉树:
在用“儿子-兄弟”法表示的树中,如果从根结点开始访问其“次子”的“次子”,所经过的结点数与下面哪种情况一样?(注意:比较的是结点数,而不是路径)
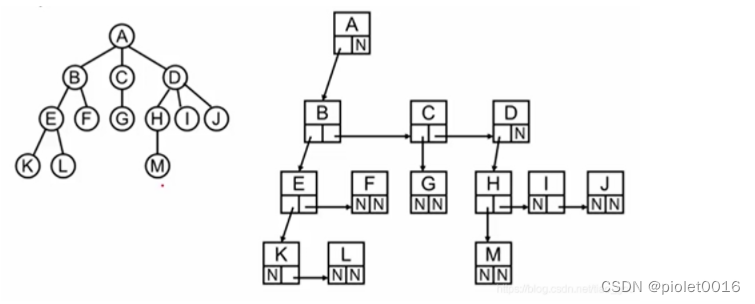
A.从根结点开始访问其“长子”的“长子”
B.从根结点开始访问其“长子”的“长子”的“长子”
C.从根结点开始访问其“长子”的“长子”的“长子”的“长子”
D.不能确定,要看具体树结构
注意不一定是二叉树,默认从左边第一个是长子,余下是次子
正确答案:C
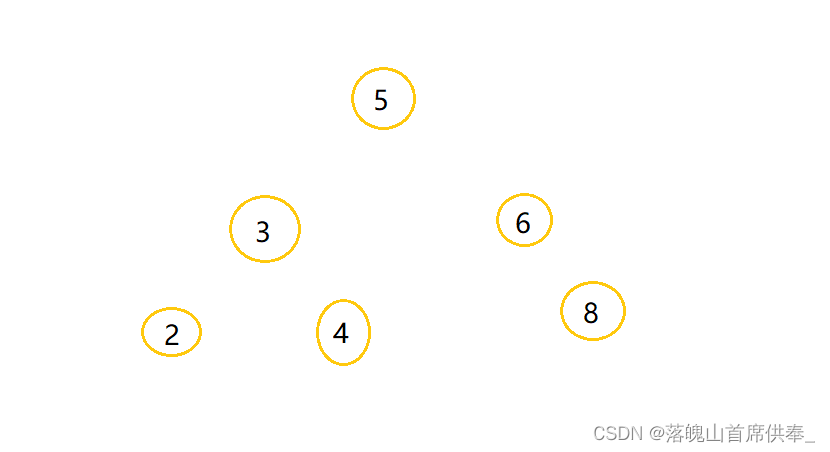
有一个m棵树的集合(也叫森林)共有k条边,问这m颗树共有多少个结点?
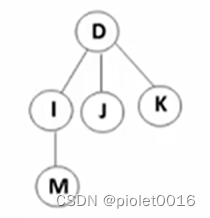
如图,该树一共有5个节点,并且有4条边,对应对于根节点的四个子节点。因为根节点是没有边的。
每个树都有一个根节点,所以m颗树,一共有m个根节点,再加上一共有k条边,有k个子节点,总共m+k个节点。
在分量1~11的数组中按从小到大顺序存放11个元素,如果用顺序查找和二分查找分别查找这11个元素,哪个位置的元素在这两种方法的查找中总次数最少?
A.1
B.2
C.3
D.6
答案:A:
注意是求和
在分量1~11的数组中按从小到大顺序存放11个元素,如果进行二分查找,查找次数最少的元素位于什么位置?
A.1
B.5
C.6
D.11
答案:C
注意不是从0开始排
一棵度(节点的度:依次节点为根节点的子树个数;树的度:树的所有节点中最大的度数)为 m的树有n个节点。若每个节点直接用m个链指向相应的儿子,则表示这个树所需要的总空间是n*(m+1) (假定每个链以及表示节点的数据域都是一个单位空间).。当采用儿子/兄弟(First Child/Next Sibling)表示法时,所需的总空间是:
A.3n
B.2n
C.n*m
D.n*(m-1)
答案:A
首先理解题干表示这个树所需要的总空间是n*(m+1),拆开更好理解:
n * m条链 + n个节点
现在考虑儿子/兄弟表示法,把n个节点串联起来,因为每个节点都有两个部分组成,一个是指向下一个兄弟节点,一个是指向子节点,所以在树中,每个节点有两条链,加上n个节点本身,一共需要3n个空间。
有一颗二叉树,其有两个儿子的结点个数为15个,只有一个儿子的结点个数为32个,问该二叉树的叶子结点个数是多少?
A.15
B.16
C.17
D.32
首先存在关系 n0 = n2 + 1 ,即叶结点个数等于有2个儿子的结点个数+1
所以15 + 1 = 16
如果一个完全二叉树最底下一层为第六层(根为第一层)且该层共有8个叶结点,那么该完全二叉树共有多少个结点?
A.31
B.39
C.63
D.71
对于一颗完全二叉树,其叶节点的数量等于最后一层节点数量的总和。因此,该完全二叉树共有8个叶节点,则最后一层共有8个节点。而对于完全二叉树,从根节点到倒数第二层为满二叉树,且节点数量为2^(h-1)-1,其中h为完全二叉树的高度。因此,该完全二叉树的高度为6,则从根节点到倒数第二层共有2^(6-1)-1=31个节点。又因为最后一层共有8个节点,则该完全二叉树共有31+8=39个节点。因此,答案为选项B:39。