广搜的优化技巧(备赛中)

news2024/9/21 23:50:42

A.电路维修

 

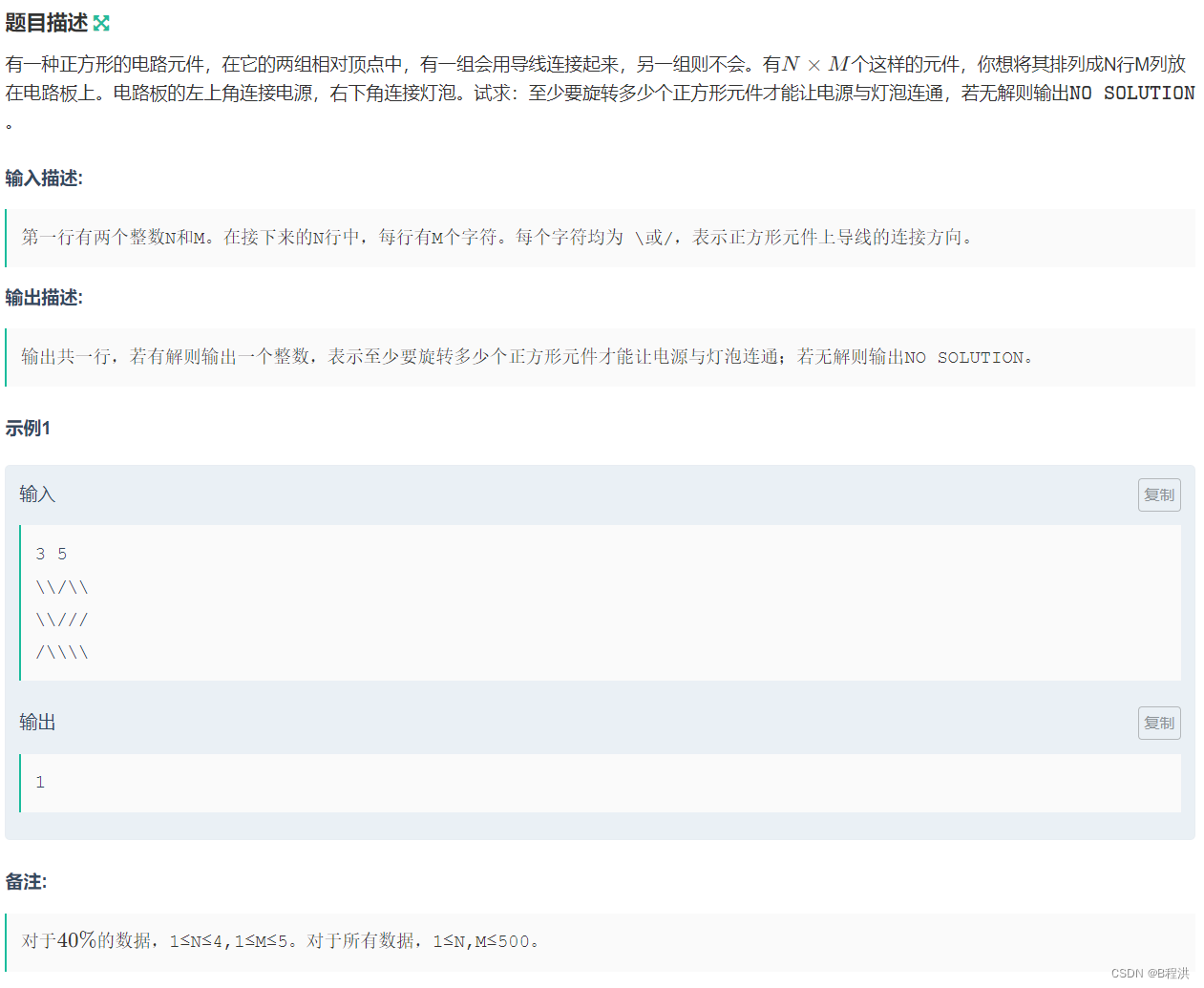
这道题我们对于每一个点都有四个方向，分别为

char op[]={"\\/\\/"};

如果我们当前点到下一个点的方向不是对应的方向时我们的distance就加1，因为我们要求最优距离，所以我们采取一个小贪心的法则，每一次我们将距离为0(此处意思就是不需要改变就可以到达)放在队首，我们将距离为1的放在队尾(此处就是需要改变才可以到达)。所以我们用到了双端队列。我们对于每一次的判别只需要将其对应字符串判断是否相等即可。

	#include<bits/stdc++.h>
	using namespace std;
	int n,m;
	int maps[1000][1000];
	int visits[1000][1000];
	char str[500][500];
	int dx[4]={-1, -1, 1, 1}, dy[4]={-1, 1, 1, -1};//下一个走到的位置
	int ix[4]={-1, -1, 0, 0}, iy[4]={-1, 0, 0, -1};//下一方向的判定位置
	char op[]={"\\/\\/"};
	int bfs()
	{   deque<pair<int,int>>que;
	    memset(maps,0x3f,sizeof(maps));
	    memset(visits,0,sizeof(visits));
	    que.push_back({0,0});
	    maps[0][0]=0;
	    while(que.size())
	    {
	        auto top=que.front();
	        que.pop_front();
	        //cout<<top.first<<" "<<top.second<<endl;
	        if(visits[top.first][top.second]==1)continue;
	        visits[top.first][top.second]=1;
	        for(int i=0;i<4;i++)
	        {
	            int a=top.first+dx[i];
	            int b=top.second+dy[i];
	            if(a<0||a>n||b<0||b>m) continue;
	            int zx=top.first+ix[i];
	            int zy=top.second+iy[i];
	            int d=maps[top.first][top.second]+(str[zx][zy]!=op[i]);
	            if(d<maps[a][b])
	            {
	               maps[a][b]=d;
	               if(str[zx][zy]!=op[i])
	               {
	                   que.push_back({a,b});
	               }
	               else if(str[zx][zy]==op[i])
	               {
	                   que.push_front({a,b});
	               }
	            }
	        }
	    }
	    return maps[n][m];

	}
	int main()
	{
        scanf("%d%d", &n, &m);
        for (int i = 0; i < n; i ++ ) scanf("%s", str[i]);
	    if((n+m)&1)
	    {
	        cout<<"NO SOLUTION"<<endl;

	    }
	    else
	    {
	        cout<<bfs();
	    }
	}

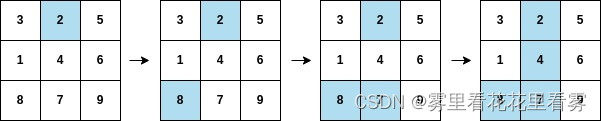
B.魔板 

 

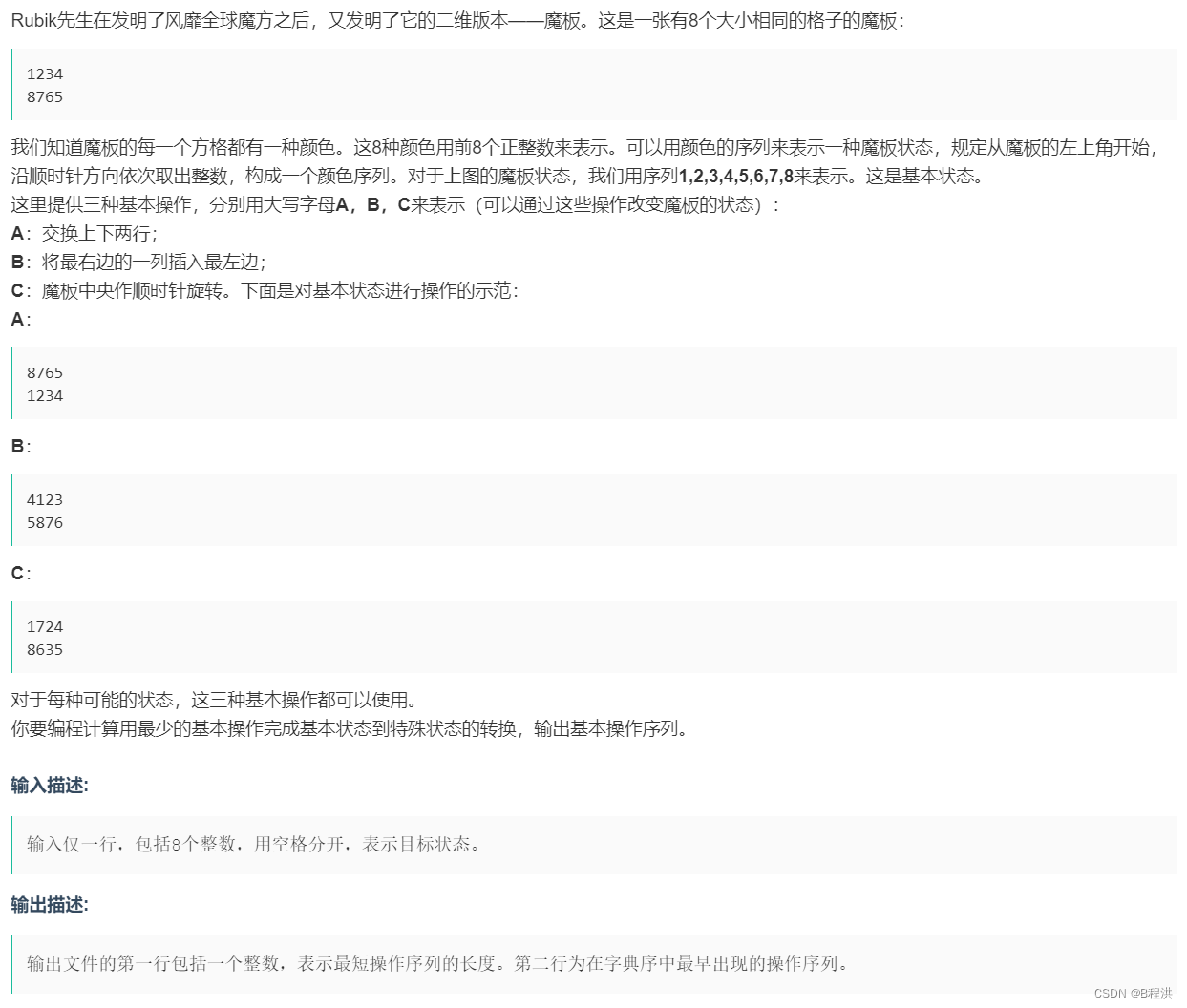
这道题我们采取了状态压缩BFS，我们把我们要更改的两个序列合成一个大字符串，之后我们对于每一步我们都要进行状态的改变进行BFS遍历直到满足情况后退出即可。我们在这里建议用map用来储存当前字符串的状态。

并且我们要想好对应状态改变的方法。

string move0(string t)
{
    for(int i = 0; i < 4; i ++ ) swap(t[i], t[7-i]);
    return t;
}

string move1(string t)
{
    for(int i = 0; i < 3; i ++ ) swap(t[i], t[3]);
    for(int i = 7; i >= 5; i -- ) swap(t[i], t[4]);
    return t;
}

string move2(string t)
{
    swap(t[1], t[2]), swap(t[5], t[6]), swap(t[1], t[5]);
    return t;
}

之后我们按BFS遍历即可。

#include <bits/stdc++.h>
using namespace std;
unordered_map<string, int> dist;
unordered_map<string, pair<char, string>> pre;//这里我们存我们对应字符串的改变方法
string start, ed, res;

string move0(string t)
{
    for(int i = 0; i < 4; i ++ ) swap(t[i], t[7-i]);
    return t;
}

string move1(string t)
{
    for(int i = 0; i < 3; i ++ ) swap(t[i], t[3]);
    for(int i = 7; i >= 5; i -- ) swap(t[i], t[4]);
    return t;
}

string move2(string t)
{
    swap(t[1], t[2]), swap(t[5], t[6]), swap(t[1], t[5]);
    return t;
}

void bfs()
{
    dist[start] = 0;
    queue<string> q;
    q.push(start);
    while (q.size())
    {
        auto t = q.front();
        q.pop();
        string m[3];
        m[0] = move0(t);
        m[1] = move1(t);
        m[2] = move2(t);
        for (int i = 0; i < 3; i ++ )
        {
            if(!dist.count(m[i]))
            {
                q.push(m[i]);
                dist[m[i]]=dist[t]+1;
                pre[m[i]]={'A'+i,t};
            }
        }
    }
}

int main()
{
    for (int i = 0; i < 8; i ++ )
    {
        char x; 
        cin >> x;
        ed += x;
        start += char(i + '1');
    }
    bfs();
    cout << dist[ed] << endl;
    if (dist[ed])
    {
        while (ed != start)
        {
            res = pre[ed].first + res;
            ed = pre[ed].second;
        }    
        cout << res << endl;
    }
    return 0;
}

C.Knight Moves

 

简单BFS，BFS能使其值最优DFS会超时也会使值不为最优，这道题恰恰体现了广搜与深搜的不同。和广搜的优点。这道题的具体实现过程就是简单的BFS，移动到终点时返回其最优值即可。

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int>pi;
int vaule[310][310];
const int dx[8]={2,1,-1,-2,-2,-1, 1, 2};
const int dy[8]={1,2,2 ,1, -1,-2,-2,-1};
void bfs()
{
    memset(vaule,0,sizeof(vaule));
    int id;cin>>id;
    int bex,bey;cin>>bex>>bey;
    int enx,eny;cin>>enx>>eny;
    queue<pi>que;
    que.push({bex,bey});
    vaule[bex][bey]=0;
    while(!que.empty())
    {
        pi top=que.front();
        que.pop();
        int tx=top.first;
        int ty=top.second;
        if(tx==enx&&ty==eny)//到终点直接返回即可
        {
             cout<<vaule[enx][eny]<<endl;
            return ;
        }
        for(int i=0;i<8;i++)
        {
            int mx=tx+dx[i];
            int my=ty+dy[i];
            if(mx<0||mx>=id||my<0||my>=id||vaule[mx][my])continue;
            vaule[mx][my]=vaule[tx][ty]+1;
            que.push({mx,my});
            
        }
    }
    
}
int main()
{
    int num;cin>>num;
    while(num--)
    {
        bfs();
    }
}

D.棋盘游戏

 

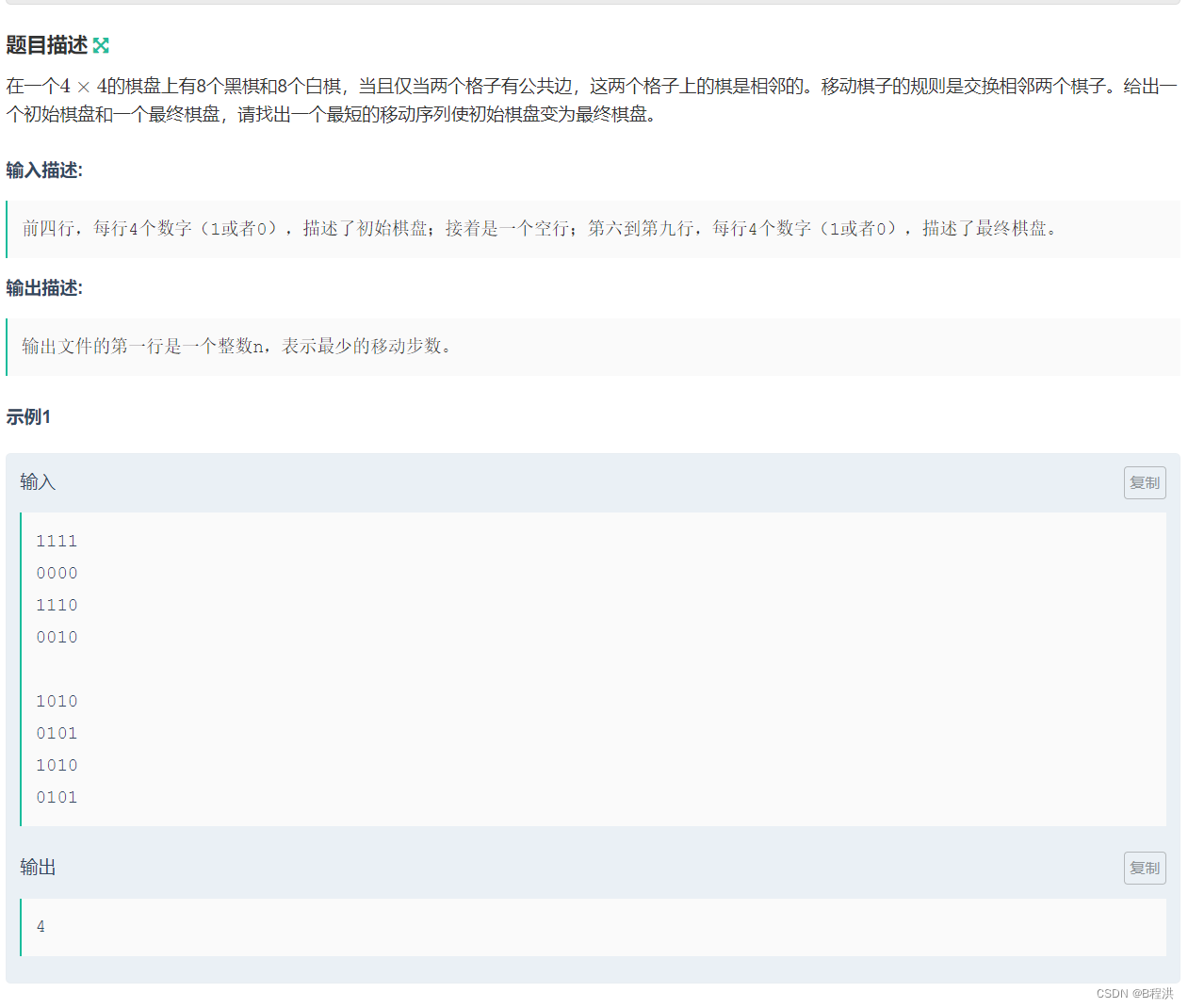
题目类似于上面第二个题也是对其进行状态压缩，然后进行广搜，充分的体现了广搜的优势，在这道题中如果要移动的棋子是相同的我们就continue；之后就是简单的BFS了。

#include<bits/stdc++.h>
using namespace std;
map<string,int>maps;
typedef pair<int,int>pi;
pi p[4]={{0,1},{1,0},{0,-1},{-1,0}};//棋子交换位置
string be;
string en;
int bfs()
{
    queue<string>que;
    que.push(be);
    while(!que.empty())
    {
        string t=que.front();
        if(t==en)return maps[en];//依旧如此，到达终点直接返回最优值。
        que.pop();
        for(int i=0;i<t.size();i++)
        {
            for(int i1=0;i1<4;i1++)
            {
                int x=i/4+p[i1].first;
                int y=i%4+p[i1].second;
                if(x<0||x>3||y<0||y>3||t[i]==t[4*x+y])continue;
                string xs=t;
                char l=xs[i];
                xs[i]=xs[4*x+y];
                xs[4*x+y]=l;
                if(maps[xs]==0)
                {
                    maps[xs]=maps[t]+1;
                    que.push(xs);
                }
            }
        }


	}
	return -1;
}
int main()
{
    for(int i=0;i<4;i++)//状态压缩
    {
        string h;cin>>h;
        be.append(h);
    }
    for(int i=0;i<4;i++)
    {
        string h;cin>>h;
        en.append(h);
    }
    cout<<bfs();
}

E.Keyboarding

 

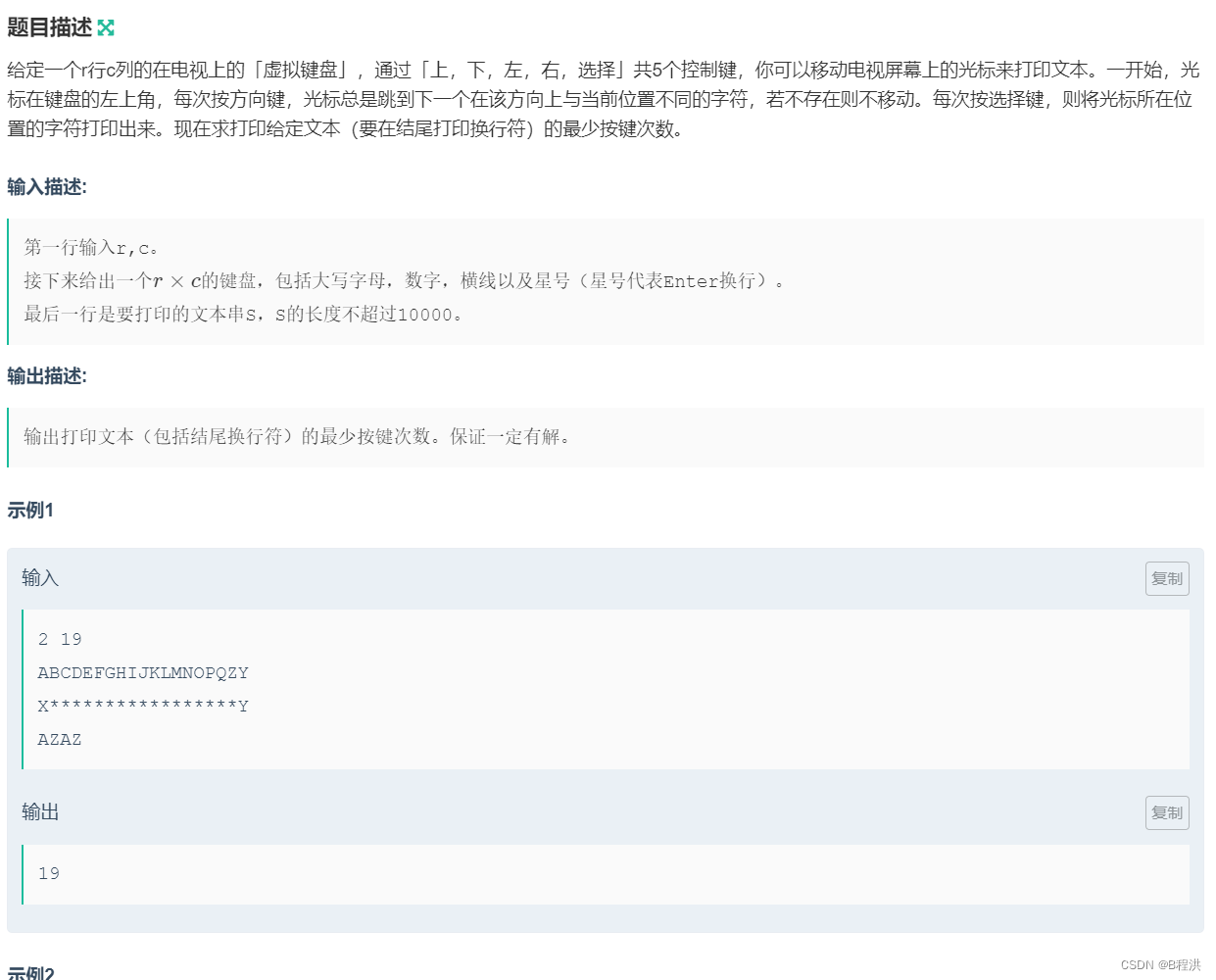
该合集中最抽象的一个题，对于这道题我们要采取预处理的方式进行，我们对于每一个预处理就是对应的每一个方向能到达不同的字符位置处为一个标记。

         for(int i=1;i<=n;i++)
	     {
		  for(int i1=1;i1<=m;i1++)
		   {
			 for(int k=0;k<4;k++)
			 {
			  int x=i+dx[k];
			  int y=i1+dy[k];
			  while(kw[i][i1]==kw[x][y])//移动到不同的字符位置处
			  {
	            x+=dx[k];y+=dy[k];
			  }
			  if(x<=0||x>n||y<=0||y>m)//越界情况
			  {
			  	n1[i][i1][k]={i,i1};
			  }
			  else
			  {
			  	n1[i][i1][k]={x,y};//我们可以移动到不同字符的位置处
			  }
			 }
		   }
		 }

然后就进行BFS遍历过程，我们对于每一层我们都要保留最优的情况当我们遍历到当前字符时我们一定是在之前就将最优的保留下来，之后当再次遍历到那个位置出同样也保留最优情况。

#include<bits/stdc++.h>
using namespace std;
char kw[100][100],en[10010];
int n,m;
int len;
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};
struct node
{
	int x,y,dis,stp;//dis为移动步数//stp为按键盘次数，每一次遍历到指定位置进行按键
};
typedef pair<int,int>pi;
pi n1[100][100][4];
int v[100][100];//保留移动最优解
int bfs()
{
	queue<node>que;
	que.push({1,1,0,0});//最初步
	while(!que.empty())
	{
	  node top=que.front();
	  que.pop();
	  if(kw[top.x][top.y]==en[top.stp])//是否按下按键
	  {
	  	   if(top.stp==len)//最后按键次数直接返回
	  	    {
			 return top.dis+1;
			}
			top.dis++;//移动次数加一
			top.stp++;//按键次数加一
			v[top.x][top.y]=top.stp;//更新按键次数
			que.push(top);
			continue;
	  }
	  for(int i=0;i<4;i++)
	  {
	  	   int x=n1[top.x][top.y][i].first;//该方向能移动到不同的位置
	  	   int y=n1[top.x][top.y][i].second;
	  	   if(v[x][y]<top.stp)//只针对按键数小的情况
	  	   {
			 v[x][y]=top.stp;
			 que.push({x,y,top.dis+1,top.stp});
		   }
	  }
	}
	return 0;
}
int main()
{
	    memset(v,-1,sizeof v);
		cin>>n>>m;
		for(int i=1;i<=n;i++)
	    {
	    	   scanf("%s",kw[i]+1);
		}
		scanf("%s",en);
	    len=strlen(en);
	     en[len]='*';
	     for(int i=1;i<=n;i++)
	     {
		  for(int i1=1;i1<=m;i1++)
		   {
			 for(int k=0;k<4;k++)
			 {
			  int x=i+dx[k];
			  int y=i1+dy[k];
			  while(kw[i][i1]==kw[x][y])
			  {
	            x+=dx[k];y+=dy[k];
			  }
			  if(x<=0||x>n||y<=0||y>m)
			  {
			  	n1[i][i1][k]={i,i1};
			  }
			  else
			  {
			  	n1[i][i1][k]={x,y};
			  }
			 }
		   }
		 }
		cout<<bfs();
}

F.移动玩具

 

依旧是状态压缩BFS与前面那几个题一个思路与方法。

#include<bits/stdc++.h>
using namespace std;
string begins;
string endx;
int dx[]={1,-1,0,0};
int dy[]={0,0,1,-1};
map<string,int>dis;
int main()
{
   for(int i=1;i<=4;i++)
   {
   	string a;cin>>a;
   	begins.append(a);
   }
   for(int i=1;i<=4;i++)
   {
   	string a;cin>>a;
   	endx.append(a);
   }
   queue<string>que;
   que.push(begins);
   dis[begins]=0;
   if(begins==endx)
   {
   	cout<<0<<endl;
   	return 0;
   }


		 while(!que.empty())
		 {
		  string z=que.front();
		  que.pop();
		  for(int i=0;i<z.size();i++)
		   {

			for(int i1=0;i1<4;i1++)
			 {
			  string h=z;
			  int x1=i/4+dx[i1];
			  int y1=i%4+dy[i1];
			  if(x1<0||x1>3||y1<0||y1>3||h[i]==h[x1*4+y1])continue;
			  swap(h[i],h[x1*4+y1]);
			  if(dis[h]==0)
			   {
			   	que.push(h);
			    dis[h]=dis[z]+1;
			   }
			   if(h==endx)
			   {
				 cout<<dis[h]<<endl;
				 return 0;
			   }
			 }
		   }
		 }

}

 

G.山峰和山谷

 

此题出的很有趣，就是在搜索过程中如果出现边界值同时大于和小于该遍历值的情况就是 既不是山峰也不是山谷，而当边界值大于我们当前遍历的值时我们当前遍历的值是山谷，反之则是山峰，我们要利用BFS的边界覆盖性质对其进行广搜，然后判断其边界的情况。

#include<bits/stdc++.h>
#define int long long
using namespace std;
int visit[1010][1010];
int maps[1010][1010];
int dx[]={0,0,1,-1,-1,1,1,-1};
int dy[]={1,-1,0,0,1,-1,1,-1};
int p,v;
int n;
int res1=0,res2=0;
typedef pair<int,int>pi;
void bfs(int x,int y)
{
	queue<pi>que;
	que.push({x,y});
	visit[x][y]=1;
    while(!que.empty())
    {
    	pi top=que.front();
    	que.pop();
    	int px=top.first;
    	int py=top.second;
    	for(int i=0;i<8;i++)
    	{
		   int tx=px+dx[i];
		   int ty=py+dy[i];
		   if(tx<0||tx>=n||ty<0||ty>=n)continue;
		   if(maps[x][y]!=maps[tx][ty])//如果不同的话就进行山峰山谷的判定，同时不同的情况不用接着遍历了。
		   {
			  if(maps[x][y]<maps[tx][ty])
			  {
				p=1;
			  }
			  else v=1;
		   }
		   else if(!visit[tx][ty]&&maps[x][y]==maps[tx][ty])//只遍历相同的值
		   {
		   	  que.push({tx,ty});
			  visit[tx][ty]=1;
		   }
		}
	}
}
signed main()
{
   cin>>n;
   for(int i=0;i<n;i++)
   {
   	for(int i1=0;i1<n;i1++)cin>>maps[i][i1];
   }
   for(int i=0;i<n;i++)
   {
   	for(int i1=0;i1<n;i1++)
   	   {
   	   	   if(visit[i][i1]==0)
   	   	    {
   	   	    	p=0;v=0;
   	   	        bfs(i,i1);
   	   	        if(p==v&&p==0) res1=res2=1;//如果全遍历完了，没有边界
   	   	        else if(p*v==1)continue;//如果全为1，则既是山峰也是山谷，直接跳过
   	   	        res1+=v;//反之
   	   	        res2+=p;
			}
	   }
   }
   cout<<res1<<" "<<res2<<endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/480495.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

「神州数码DCN」SAVI在IPV6环境下的应用

「神州数码DCN」SAVI在IPV6环境下的应用

前言 介绍 ISIS&#xff0c;中间系统到中间系统的网络协议&#xff0c;最初是OSI组织为了他的CLNP&#xff08;类似于TCP/IP中的IP网络&#xff09;而设计的动态路由协议&#xff0c;后IETF对其进行修改和填充&#xff0c;现可以在TCP/IP和OSI环境中使用&#xff0c;称为&…
阅读更多...
JavaWeb学习------jQuery

JavaWeb学习------jQuery

JavaWeb学习------jQuery jQuery函数库下载 jQuery函数库下载官网&#xff1a;Download jQuery | jQuery配套资料&#xff0c;免费下载 链接&#xff1a;https://pan.baidu.com/s/1aXBfItEYG4uM53u6PUEMTg 提取码&#xff1a;6c9i 然后下载&#xff1f; 来到官网&#xf…
阅读更多...
Spark 1：Spark基础入门

Spark 1：Spark基础入门

Spark是什么 定义&#xff1a;Apache Spark是用于大规模数据&#xff08;large-scala data&#xff09;处理的统一&#xff08;unified&#xff09;分析引擎。 Spark 借鉴了 MapReduce 思想发展而来&#xff0c;保留了其分布式并行计算的优点并改进了其明显的缺陷。让中间数据存…
阅读更多...
Winform从入门到精通（36）—ColorDialog（史上最全）

Winform从入门到精通（36）—ColorDialog（史上最全）

文章目录 前言一、属性1、AllowFullOpen2、AnyColor3、Color4、FullOpen5、ShowHelp6、SolidColorOnly7、Tag二、事件1、HelpRequest前言 当我们需要设置某个控件的颜色时，并且需要弹出一个可以选择颜色的对话框时，这时候就需要使用ColorDialog 一、属性 1、AllowFullOpen…
阅读更多...
详解正则化

详解正则化

&#xff08;一&#xff09;正则化目的 防止过拟合现象&#xff0c;通过降低模型在训练集上的精度来提高其泛化能力&#xff0c;从而增加正则项 常见的降低过拟合方法 ■增加数据集的数据个数。数据量太小时&#xff0c;非常容易过拟合&#xff0c;因为 小数据集很容易精确拟…
阅读更多...
Linux线程相关函数：线程的创建、回收、退出、取消

Linux线程相关函数：线程的创建、回收、退出、取消

1. 线程号 进程号在系统中唯一&#xff0c;但线程号只在其所属进程环境中有效。 &#xff08;1&#xff09;pthread_self函数 #include<pthread.h>pthread_t pthread_self(void); /* 功能&#xff1a;获取线程号 返回值&#xff1a;调用此函数线程的ID */ pthread_se…
阅读更多...
基于ssm的论坛系统的设计与实现【附源码】

基于ssm的论坛系统的设计与实现【附源码】

基于ssm的论坛系统的设计与实现 摘 要 早期的网络论坛系统已经诞生一段时间&#xff0c;随着互联网技术的发展&#xff0c;它已经从最初的简单电子公告板系统变成了一种丰富的论坛系统社区模型。人们通过论坛系统进行信息的获取、发布和交流已经成为一种普遍的社交方式&#x…
阅读更多...
一键开关机电路

一键开关机电路

一键开关机电路&#xff0c;通常用在防止关机导致数据保存发生错误&#xff0c;特别是在写EEPROM&#xff0c;FLASH和SD卡时&#xff0c;如果正在写入数据时断电&#xff0c;可能会导致数据保存错误&#xff0c;甚至导致元件损坏。一键开关机电路是由CPU来掌控&#xff0c;决定…
阅读更多...
零基础带你认识HTML常用标签

零基础带你认识HTML常用标签

目录 HTML 结构认识 HTML 标签HTML 文件基本结构标签层次结构快速生成代码框架 HTML 常见标签注释标签标题标签&#xff1a;h1 - h6水平线 hr 标签段落标签: p换行标签: br格式化标签图片标签: imgimg 标签的其他属性 超链接标签: a 表格标签基本使用和并单元格 列表标签表单标…
阅读更多...
Compiler Lab1- 自制词法分析器

Compiler Lab1- 自制词法分析器

由于编译原理课的Lab1为自制词法分析器&#xff0c;所以笔者用C实现了一个极简的C语言词法分析器&#xff0c;用于分析C语言源代码。它可以处理关键字、标识符、整数、实数、浮点数的科学计数法表示、运算符、分隔符、字符串字面量、字符字面量、注释和预处理指令。请注意&…
阅读更多...
【五一创作】力扣刷题实录（大厂用题）—— 1. 打家劫舍

【五一创作】力扣刷题实录（大厂用题）—— 1. 打家劫舍

1. 打家劫舍 某大厂 2022 年 9 月面试题挑战&#xff08;三&#xff09; 1.1 题目描述 力扣真题地址&#xff1a;https://leetcode.cn/problems/house-robber/?envTypestudy-plan-v2 你是一个专业的小偷&#xff0c;计划偷窃沿街的房屋。每间房内都藏有一定的现金&#xff0c;…
阅读更多...
Photoshop如何使用路径与矢量工具之实例演示？

Photoshop如何使用路径与矢量工具之实例演示？

文章目录 0.引言1.制作名片2.利用钢笔工具抠出复杂图像3.制作App图标4.制作软件登录界面5.将图片切成九宫格 0.引言 因科研等多场景需要进行绘图处理&#xff0c;笔者对PS进行了学习&#xff0c;本文通过《Photoshop2021入门教程》及其配套素材结合网上相关资料进行学习笔记总结…
阅读更多...
简单搭建node后台（笔记用）

简单搭建node后台（笔记用）

毕设过程 mongodb 配置 使用node写后台一些语法运用bug关于安装一款群控软件后&#xff0c;修改了环境变量导致后台崩溃![](https://img-blog.csdnimg.cn/7c684b2e318048b3ad1db78484e10e6a.jpeg) vue管理后台 mongodb 配置 https://blog.csdn.net/weixin_43405300/article/de…
阅读更多...
Unity API详解——Vector3类

Unity API详解——Vector3类

Vector3类是用于表示三维向量的类&#xff0c;其中的x、y和z成员表示向量在三个轴上的分量。Vector3类还包含许多常用的函数&#xff0c;例如计算向量长度、向量点积和向量叉积等等。此外&#xff0c;Vector3类还具有许多方便的操作&#xff0c;例如规范化向量、向量加法、向量…
阅读更多...
数据预处理--sort乱序DICOM文件

数据预处理--sort乱序DICOM文件

我们直接从PACS系统里拷贝下来的图像&#xff0c;很多情况下是乱序的&#xff0c;随机命名的。如下图 从这个文件夹名字&#xff0c;我们只知道患者的 ID 信息&#xff0c;不知道这个图像是什么模态&#xff08;CT/MRI/Xray&#xff09;&#xff0c;也不知道扫的是哪个部位&…
阅读更多...
【电子学会】2023年03月图形化一级 -- 甲壳虫走迷宫

【电子学会】2023年03月图形化一级 -- 甲壳虫走迷宫

甲壳虫走迷宫 1. 准备工作 &#xff08;1&#xff09;绘制如图所示迷宫背景图&#xff0c;入口在左下角&#xff0c;出口在右上角&#xff0c;线段的颜色为黑色&#xff1b; &#xff08;2&#xff09;删除默认小猫角色&#xff0c;添加角色&#xff1a;Beetle&#xff1b; …
阅读更多...
Python探索性P图，四种增强方式快速玩转pillow库

Python探索性P图，四种增强方式快速玩转pillow库

嗨害大家好鸭&#xff01;我是爱摸鱼的芝士❤ 我们平时使用一些图像处理软件时&#xff0c; 经常会看到其对图像的亮度、对比度、色度或者锐度进行调整。 你是不是觉得这种技术的底层实现很高大上&#xff1f; 其实最基础的实现原理&#xff0c; 用 Python 实现只需要几行…
阅读更多...
【力扣周赛】第343场周赛

【力扣周赛】第343场周赛

【力扣周赛】第343场周赛 2660&#xff1a;保龄球游戏的获胜者题目描述解题思路 2661&#xff1a;找出叠涂元素题目描述解题思路 2660&#xff1a;保龄球游戏的获胜者 题目描述 描述&#xff1a;给你两个下标从 0 开始的整数数组 player1 和 player2 &#xff0c;分别表示玩家…
阅读更多...
系统集成项目管理工程师 笔记（第10章 项目质量管理）

系统集成项目管理工程师 笔记（第10章 项目质量管理）

文章目录 10.1.2 质量管理及其 发展史 35610.1.3 项目质量管理 35810.2.2 规划质量管理的输入 35910.2.3 规划质量管理的工具与技术 3601、成本效益分析法2、质量成本法&#xff08;一致性成本【预防、评价】 和 非一致性成本【内部、外部】&#xff09;3、七种基本质量工具&am…
阅读更多...
【AI作诗】主流平台介绍+自主搭建

【AI作诗】主流平台介绍+自主搭建

诗歌总是属于文人的浪漫&#xff0c;但随着技术的发展&#xff0c;理科生文艺起来&#xff0c;也就没文科生什么事了&#xff08;开玩笑的&#xff09;。通过本篇文章&#xff0c;笔者将给大家介绍主流的AI诗歌创作平台及如何自己搭建&#xff0c;以供大家学习参考。 技术的进…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023