E. Colorful Operations
https://codeforces.com/contest/1638/problem/E
题目描述
给你一个数组,默认初始元素为 0 ,颜色为 1,有三种操作:
Color l r c:将[l, r]区间内的颜色修改为 cAdd c x:将所有颜色为 c 的元素增加 xQuery i:打印第 i 个元素
输入描述
输入的第一行包含两个整数n和q(1≤n,q≤106) — 数组的长度以及您必须执行的查询次数。
接下来的每一个q行包含以问题陈述中描述的形式给出的查询。
输出描述
打印 Query 的结果。
样例
#1
5 8
Color 2 4 2
Add 2 2
Query 3
Color 4 5 3
Color 2 2 3
Add 3 3
Query 2
Query 5
2
5
3
#2
2 7
Add 1 7
Query 1
Add 2 4
Query 2
Color 1 1 1
Add 1 1
Query 2
7
7
8
提示
下面解释第一个样本测试。蓝色、红色和绿色分别代表颜色1,2和3。
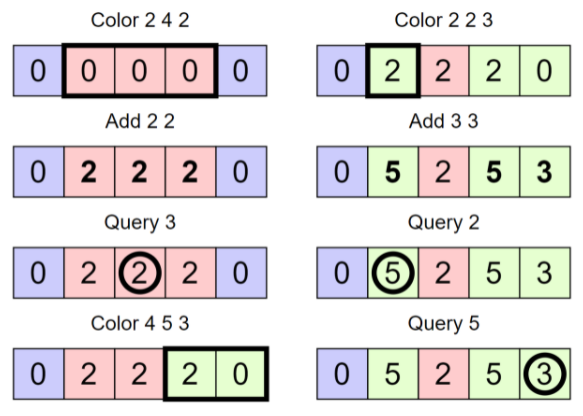
解析
个人认为本题的难点主要是如何维护这个颜色,我一开始是想用一个结点内部维护一个 color 和 val 属性,表示每个结点的颜色和值,用的是线段树,后面我发现如果一个区间内的颜色不同,那么 color 到底应该填什么呢…,val 又表示啥呢?
当然,我这是普通的线段树模板而已,才学不久,看来还是我太菜了…
回到主题:
我们先考虑单点操作,三种操作如下:
Color x c:将元素 i 的颜色修改为 cAdd c x:将所有颜色为 c 的元素增加 xQuery i:打印第 i 个元素
首先我们需要一个 L a z y [ c o l o r ] Lazy[color] Lazy[color] 来保存每个颜色的总和,因为我们总不可能遍历每一个颜色为 c 的元素都增加 x 吧?这样效率很低,可以考虑先操作,等该数的颜色发生变化时,再去更新元素的值,这就是一个延迟操作的效果。
还需要一个 c o l o r [ i ] color[i] color[i] 保持元素 i 的颜色。
对于操作 2 来说: L a z y [ c ] + = x Lazy[c] += x Lazy[c]+=x
对于操作 3 来说: A [ x ] + L a z y [ c o l o r [ x ] ] A[x] + Lazy[color[x]] A[x]+Lazy[color[x]] (输出需要加上 Lazy ,这就是延迟)
对于操作 1 来说:
A
[
x
]
+
=
L
a
z
y
[
c
o
l
o
r
[
x
]
]
A[x] += Lazy[color[x]]
A[x]+=Lazy[color[x]] (颜色准备发生改变,更新当前元素=>触发延迟操作)
c o l o r [ x ] = c color[x] = c color[x]=c (更新颜色)
A [ x ] − = L a z y [ c ] A[x] -= Lazy[c] A[x]−=Lazy[c] (因为我们输出时,我们要保证 A [ x ] + L a z y [ c o l o r [ x ] ] A[x] + Lazy[color[x]] A[x]+Lazy[color[x]] ,因此需要减去 L a z y [ c ] Lazy[c] Lazy[c] )
手动模拟一下:
【1】Add 1 7
【2】Query 1 7
【3】Add 2 4
【4】Query 2
【5】Color 1 2
【6】Query 1
====================
Lazy: 0 0 0
Color: 1 1 1
A: 0 0 0
====================
【1】Lazy[1] += 7
====================
Lazy: 7 0 0
Color: 1 1 1
A: 0 0 0
====================
【2】A[1] + Lazy[color[1]] // print 7
【3】Lazy[2] += 4
====================
Lazy: 7 4 0
Color: 1 1 1
A: 0 0 0
====================
【4】A[2] + Lazy[color[2]] // print 7
【5】A[1] += Lazy[color[1]]
color[1] = 2
A[1] -= Lazy[2]
====================
Lazy: 7 4 0
Color: 1 1 1
A: 7 0 0
--------------------
Lazy: 7 4 0
Color: 2 1 1
A: 7 0 0
--------------------
Lazy: 7 4 0
Color: 2 1 1
A: 3 0 0
====================
【6】A[1] + Lazy[color[1]] // print 7
明白了单点操作,回来看看区间操作:
采用线段树和LazyTag的方式来进行实现。
colorVal[color]:同上面的 Lazy
需要一个结点,里面维护如下元素:
same:该区间的所有元素是否相同color:该结点的颜色,当 same 为 true 时,表示该区间内所有的颜色lazy:懒标记,同时也作为该元素的值
对于操作 2 和 操作 3 来说,其实和单点的是一样。对于操作 1 来说也差不多。
对于操作 1:只修改同一种颜色的区间,否则就一定往下找,最后一个点一定为 true
AC Code
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static final int MAX = 1000005;
static long[] colorVal = new long[MAX];
static Node[] T = new Node[MAX << 2];
static int n, m;
public static void main(String[] args) throws Exception {
n = nextInt(); m = nextInt();
build(1, 1, n);
while(m-- != 0) {
String opt = nextStr();
if(opt.equals("Color")) update(1, nextInt(), nextInt(), nextInt());
else if(opt.equals("Add")) colorVal[nextInt()] += nextInt();
else if(opt.equals("Query")) {
int v = nextInt();
out.println(query(1, v, v));
}
}
out.flush();
}
public static void build(int p, int start, int end) {
T[p] = new Node(start, end);
if(start == end) {
T[p].color = 1;
T[p].same = true;
return;
}
int mid = (start + end) / 2;
build(L(p), start, mid);
build(R(p), mid + 1, end);
pushUp(p);
}
public static void update(int p, int start, int end, int k) {
// 只修改同一种颜色的区间,否则就一直往下找,最后一个点一定为 true
if(start <= T[p].left && end >= T[p].right && T[p].same) {
T[p].lazy += colorVal[T[p].color];
T[p].color = k;
T[p].lazy -= colorVal[T[p].color];
return;
}
pushDown(p);
int mid = (T[p].left + T[p].right) / 2;
if(start <= mid) update(L(p), start, end, k);
if(end > mid) update(R(p), start, end, k);
pushUp(p);
}
public static long query(int p, int start, int end) {
long res = 0;
if(start <= T[p].left && end >= T[p].right)
return T[p].lazy + colorVal[T[p].color];
pushDown(p);
int mid = (T[p].left + T[p].right) / 2;
if(start <= mid) res += query(L(p), start, end);
if(end > mid) res += query(R(p), start, end);
return res;
}
public static void pushDown(int p) {
// 因为我们修改的是同一种颜色的区间,因此也对同一种颜色的区间下传
if(T[p].same) {
T[L(p)].lazy += T[p].lazy;
T[R(p)].lazy += T[p].lazy;
T[L(p)].color = T[p].color;
T[R(p)].color = T[p].color;
T[p].lazy = 0;
}
}
public static void pushUp(int p) {
// 只更新同一种颜色的区间
if(T[L(p)].same && T[R(p)].same && T[L(p)].color == T[R(p)].color) {
T[p].same = true;
T[p].color = T[R(p)].color;
} else {
T[p].same = false;
}
}
public static int L(int p) { return p<<1; };
public static int R(int p) { return p<<1|1; };
public static int nextInt() throws Exception {
st.nextToken();
return (int) st.nval;
}
public static String nextStr() throws Exception {
st.nextToken();
return st.sval;
}
}
class Node {
int left, right;
int color; // 该区间颜色
long lazy; // lazyTag
boolean same; // 该区间内的颜色是否完全相同
public Node(int left, int right) {
this.left = left;
this.right = right;
}
}