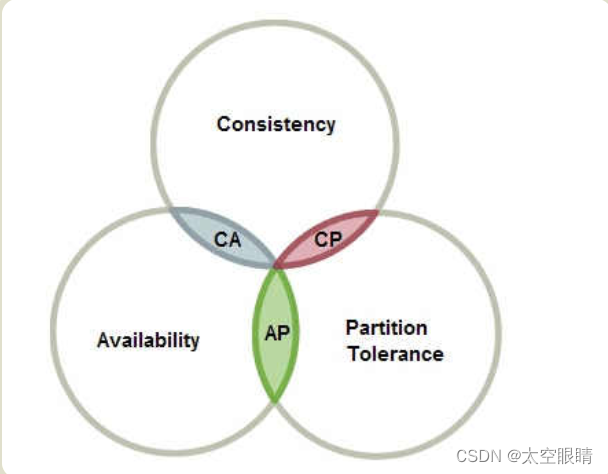
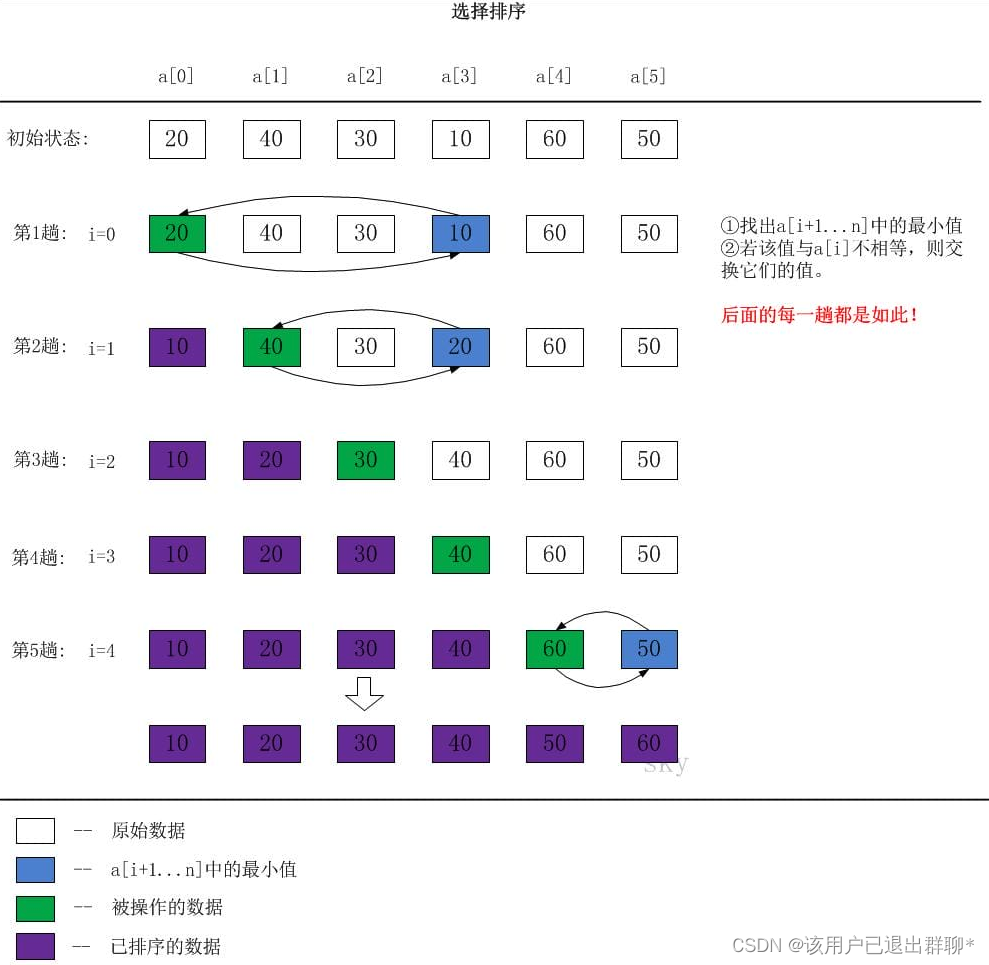
现在JAVASE中HashMap中底层源码是由数组+链表+红黑树进行设计的,然后很多地方也是用到红黑树,这里单独对红黑树数据结构进行简单的介绍。
目录
红黑树概念
红黑树的性质
自平衡规则
代码
红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
二叉查找树,也称有序二叉树(ordered binary tree),或已排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 任意节点的左、右子树也分别为二叉查找树。 没有键值相等的节点(no duplicate nodes)。 因为一棵由n个结点随机构造的二叉查找树的高度为lgn,所以顺理成章,二叉查找树的一般操作的执行时间为O(lgn)。但二叉查找树若退化成了一棵具有n个结点的线性链后,则这些操作最坏情况运行时间为O(n)。红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点),任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的。
自平衡规则
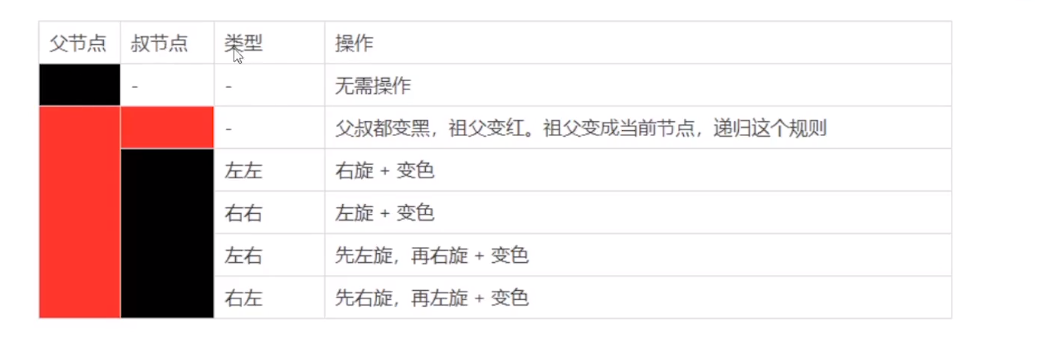
代码
红黑树插入
插入操作包括两部分工作:一查找插入的位置;二插入后自平衡。查找插入的父结点很简单,跟查找操作区别不大:
从根结点开始查找;
若根结点为空,那么插入结点作为根结点,结束。
若根结点不为空,那么把根结点作为当前结点;
若当前结点为null,返回当前结点的父结点,结束。
若当前结点key等于查找key,那么该key所在结点就是插入结点,更新结点的值,结束。
若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤4;
若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤4;

package com.example.tree;
public class RBTree<K extends Comparable<K>,V> {
private static final boolean RED=true;
private static final boolean BLACK=false;
private RBNode root;
static class RBNode<K extends Comparable<K>,V>{
private RBNode parent;
private RBNode left;
private RBNode right;
private boolean color;
private K key;
private V value;
public RBNode getParent() {
return parent;
}
public void setParent(RBNode parent) {
this.parent = parent;
}
public RBNode getLeft() {
return left;
}
public void setLeft(RBNode left) {
this.left = left;
}
public RBNode getRight() {
return right;
}
public void setRight(RBNode right) {
this.right = right;
}
public boolean isColor() {
return color;
}
public void setColor(boolean color) {
this.color = color;
}
public K getKey() {
return key;
}
public void setKey(K key) {
this.key = key;
}
public V getValue() {
return value;
}
public void setValue(V value) {
this.value = value;
}
public RBNode() {
}
public RBNode(RBNode parent, RBNode left, RBNode right, boolean color, K key, V value) {
this.parent = parent;
this.left = left;
this.right = right;
this.color = color;
this.key = key;
this.value = value;
}
}
//获取父节点
private RBNode parentof(RBNode rbNode){
return rbNode!=null?rbNode.parent:null;
}
//判断是否为红色
private boolean isRed(RBNode rbNode){
return rbNode.color==RED?true:false;
}
private boolean isBlack(RBNode rbNode){
return rbNode.color==RED?false:true;
}
private void setRed(RBNode rbNode){
if(rbNode!=null){
rbNode.color=RED;
}
}
private void setBlack(RBNode rbNode){
if(rbNode!=null){
rbNode.color=BLACK;
}
}
public void inOrder(){
inOrder(this.root);
}
//中序打印
public void inOrder(RBNode rbNode){
if(rbNode!=null){
inOrder(rbNode.left);
System.out.print(rbNode.key+" ");
inOrder(rbNode.right);
}
}
//左旋
private void leftRotate(RBNode rbNode){
RBNode right = rbNode.right;
rbNode.right=right.left;
if(right.left!=null){
right.left.parent=rbNode;
}
if(rbNode.parent!=null){
right.parent=rbNode.parent;
if(rbNode.parent.left==rbNode)
rbNode.parent.left=right;
if(rbNode.parent.right==rbNode)
rbNode.parent.right=right;
}
else {
this.root=right;
}
rbNode.parent=right;
right.left=rbNode;
}
//右旋
private void rightRotate(RBNode rbNode){
RBNode left = rbNode.left;
rbNode.left=left.right;
if(left.right!=null)
left.right.parent=rbNode;
if(rbNode.parent!=null){
left.parent=rbNode.parent;
if(rbNode.parent.left==rbNode)
rbNode.parent.left=left;
if(rbNode.parent.right==rbNode)
rbNode.parent.right=left;
}
else {
this.root=left;
}
rbNode.parent=left;
left.right=rbNode;
}
public void insert(K key,V value){
RBNode node=new RBNode();
node.setKey(key);
node.setValue(key);
node.setColor(RED);
insert(node);
}
private void insert(RBNode rbNode){
RBNode parent=null;
RBNode x=this.root;
while (x!=null){
parent=x;
int i = rbNode.key.compareTo(x.key);
if(i>0){
x=x.right;
}
else if(i==0){
x.setValue(rbNode.getValue());
return;
}
else {
x=x.left;
}
}
rbNode.parent=parent;
if(parent!=null){
int i = rbNode.key.compareTo(parent.key);
if(i>0){
parent.right=rbNode;
}
else {
parent.left=rbNode;
}
}else {
this.root=rbNode;
}
insertFixup(rbNode);
}
private void insertFixup(RBNode node){
this.root.setColor(BLACK);
RBNode parent = parentof(node);
RBNode gparent = parentof(parent);
if(parent!=null&&isRed(parent)){
RBNode uncle=null;
if(parent==gparent.left){
uncle=gparent.right;
if (uncle != null && isRed(uncle)) {
setBlack(parent);
setBlack(uncle);
setRed(gparent);
insertFixup(gparent);
return;
}
if(uncle==null||isBlack(uncle)){
if(node==parent.left){
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
return;
}
if(node==parent.right){
leftRotate(parent);
insertFixup(parent);
return;
}
}
}
else {
uncle=gparent.right;
if (uncle != null && isRed(uncle)) {
setBlack(parent);
setBlack(uncle);
setRed(gparent);
insertFixup(gparent);
return;
}
if(uncle==null||isBlack(uncle)){
if(node==parent.right){
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
return;
}
if(node==parent.left){
rightRotate(parent);
insertFixup(parent);
return;
}
}
}
}
}
注:
Key extends Comparable<Key>:这里相当于使用泛型,但是这里的泛型Key有限制,表示必须实现Comparable<Key>这个接口才能当成参数传递;如Java自带的Integer、String都符合这个要求;而且这种写法只能当成类的泛型使用,这里其实是将泛型Key擦除到它的一个边界。
而Comparable 本身是一个接口,如果一个类如:class Key implements Comparable<Integer>{} 也是Comparable的子类,即前后可以不一致;而且Comparable本身一般不做泛型使用;另外Comparable可以当成方法的参数使用。

![[架构之路-176]-《软考-系统分析师》-17-嵌入式系统分析与设计 -1- 实时性(任务切换时间、中断延迟时间、中断响应时间)、可靠性、功耗、体积、成本](https://img-blog.csdnimg.cn/f73c83a0b3df47f7abd1efc69d050b1c.png)