不要纠结，干就完事了，熟练度很重要！！！多练习，多总结！！！

前缀和数组

LeetCode 303. 区域和检索 - 数组不可变

解题思路

核心思路是我们 new 一个新的数组preSum出来，preSum[i]记录nums[0…i-1]的累加和，看图 10 = 3 + 5 + 2：

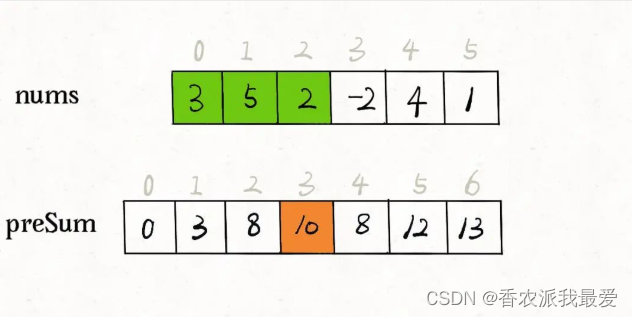
看这个preSum数组，如果我想求索引区间[1, 4]内的所有元素之和，就可以通过preSum[5] - preSum[1]得出。
这样，sumRange函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数O(1)。

代码实现

class NumArray {

    int[] preSum;
    public NumArray(int[] nums) {
        preSum = new int[nums.length +1];

        for(int i = 1;i < preSum.length;i++){
            preSum[i] = preSum[i-1]+nums[i-1];
        }
    }
    
    public int sumRange(int left, int right) {
        return preSum[right+1]-preSum[left];
    }
}

LeetCode 304. 二维区域和检索 - 矩阵不可变

解题思路

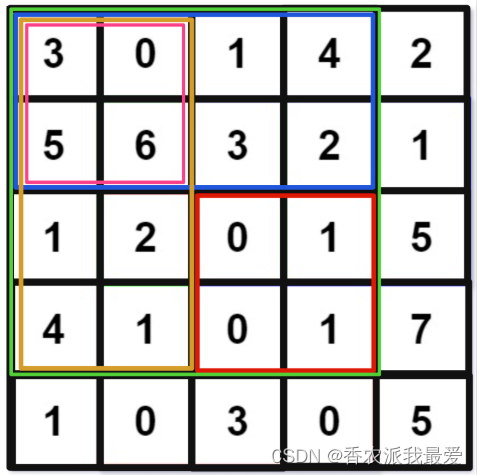
如果我想计算红色的这个子矩阵的元素之和，可以用绿色矩阵减去蓝色矩阵减去橙色矩阵最后加上粉色矩阵，而绿蓝橙粉这四个矩阵有一个共同的特点，就是左上角就是(0, 0)原点。

那么我们可以维护一个二维preSum数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和。

代码实现

class NumMatrix {
    int[][] preSum;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        preSum = new int[m+1][n+1];

        for(int i = 1;i <= m;i++){
            for(int j = 1;j <= n;j++){
                preSum[i][j] = preSum[i-1][j]+preSum[i][j-1]+matrix[i-1][j-1]-preSum[i-1][j-1];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2+1][col2+1]-preSum[row2+1][col1]-preSum[row1][col2+1]+preSum[row1][col1];
    }
}

总结

本题来源于Leetcode中 归属于数组、链表类型题目。
同许多在算法道路上不断前行的人一样，不断练习，修炼自己！
如有博客中存在的疑问或者建议，可以在下方留言一起交流，感谢各位！

觉得本博客有用的客官，可以给个点赞+收藏哦！ 嘿嘿

喜欢本系列博客的可以关注下，以后除了会继续更新面试手撕代码文章外，还会出其他系列的文章！