目录
一、数的类型
二.数值的相互转换
三.机器数的表示
四.机器数的运算--补码加减法
五.运算结果溢出的判断。
六.数据的编码
一、数的类型
1.十进制(Decimal)
基数为10,用0、1、2、3、4、5、6、7、8、9十个数码表示数值,采用逢10进一,位置在第i位的权值为10^i,基数为10,用字母D表示,经常省略不写。
序位:从挨着小数点0开始数(第几位)
权值:位置在第i位的权值为10i
2.二进制(Binary)
在计算机内部,任何数据都用0和1表示。“0”代表低电平,“1”代表高电平。 二进制表示法中基数为2,只用0、1两个数码来表示数值,逢二进一,位置在第i位的权值为2𝑖,用字母B表示。
3.八进制(Octal)
八进制表示法中基数为8,采用0、1、2、3、4、5、6、7八个数字,逢八进一,位置在第i位的权值为8^i,用字母o表示。
4.十六进制(Hexadecimal)
十六进制表示法中基数为16 = 2^4,用数字0-9和字母A、B、C、D、E、F(对应十进制数的10-15)来表示,逢十六进一,位置在第i位的权值为16^i,用字母H表示。
有十六个数码:0~9,A(1010),B(1011),C(1100),D(1101),E(1110),F(1111)
二.数值的相互转换
1.非十进制数 --> 十进制数 规则
熟悉各整数和小数次方,多项式展开求和
(1)二进制 --> 十进制数
二进制数转换为十进制数,将二进制数按“权”展开相加即可。
例如:1011.01B
= 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 + 0*2^-1 + 1*2^-2
= 8 + 0 + 2 + 1 + 0 + 0.25
= 11.25D

(2)八进制 --> 十进制数

(3)十六进制 --> 十进制数

2.十进制数 --> 非十进制数
十进制数转换为非十进制,要把整数部分和小数部分分别进行转换,然后再把转换结果进行相加。
整数转换采用除基数取余法:用基数不断地去除要转换的数,直到商为0,再将每一步所得的余数,按逆序排列,便为转换结果。(除进制数取余数,倒序输出)
小数转换采用用基数取整法:每次用基数与小数部分相乘,取乘积的整数部分,再取其小数部分乘2直到小数部分为0。将所取整数顺序放在小数点后即为转换结果。(乘进制数取整,顺序输出)
说明:有些十进制小数不能精确转换为二进制小数,即乘积的小数部分永远不能为0,此时应根据精度要求,转换到所需位数即可。
(1)十进制数 --> 二进制数
整数部分:除2(基数)取余
小数部分:乘2(基数)取整

(2)十进制数 --> 八进制数
整数部分:除8(基数)取余
小数部分:乘8(基数)取整
例如:
796(10) = 1434(8)
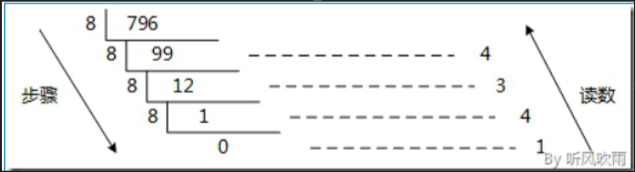
(3)十进制数 --> 十六进制数
整数部分:除16(基数)取余
小数部分:乘16(基数)取整
例如:796(10) = 31(16)

小结:十进制 --> 非十进制数
以上几种进制的整数部分转换原理都是除进制数取余数,倒序输出。小数部分转换原理都是乘进制数取整数部分,再将整数部分顺序输出。
3.二进制 <--> 其他进制
由于二进制的基数是2,而八进制的基数是8=2^3,一位八进制数字正好可以对应3位二进制数字;十六进制的基数为16=2^4,即一位十六进制数字正好对应4位二进制数字,因此他们之间的转换非常简便。
(1)二进制 <--> 八进制
每3位二进制数表示1位八进制数。
二进制到八进制采用“三位化一体”的方法,把要转换的二进制数,从小数点开始向两边分别进行分组。转换为八进制时,向左每三位为一组,向右每三位为一组,向左不是三位的,从左边补0;向右不足三位的, 从右边补0。
10110.1011(2) = 26.54 (8)

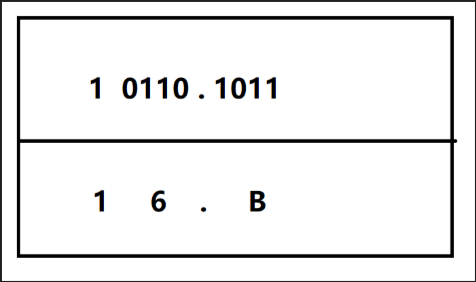
(2)二进制 <--> 十六进制
二进制到十六进制采用“四位化一体”的方法,把要转换的二进制数,从小数点开始向两边分别进行分组。转换为十六进制时,向左每四位为一组,向右每四位为一组,向左不足四位的,从左边补0;向右不足四位的,从右边补0
10110.1011(2) = 16.B (16)
4.八、十六进制 --> 二进制
采用“一位化三(四)位的方法:即按顺序写出每位八进制(十六进制)数字所对应的三位(四位)二进制数,所得结果即为对应的二进制数。(最高位的0和小数点最末位的0可以略去)
(1)八进制数转换成二进制
原理:八进制数的一位是二进制数的三位
例如:将(356.2)8 转换为二进制
写出各位数字对应的三位二进制数,组合成二进制数。
(365.2)8 = (011 101 110 . 010)2
(2)十六进制数转换成二进制
原理:十六进制数的一位是二进制数的四位
例如:将十六进制3B6.9H转换为二进制数:
3B6.9H = 0011 1011 0110.1001B
5.八进制与十六进制之间的转换
这两者之间的转换可以借助十进制或者二进制完成,可以先将八进制转换成十进制或二进制,再转换成十六进制。通过间接转换来实现。
三.机器数的表示
在计算机中,只有数码1和0两种不同的状态,对于一个数的正、负号,两种不同的状态,约定正数的符号用“0”表示,负数的符号用“1”表示,将符号位放在数的最左边,即最高位,这种计算机用来表示数的形式叫机器数,而把对应于该机器数的带正负符号的算数值叫真值。
1.机器数:一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0,负数为1
比如:十进制的数+3,计算机字长为8位,转换成二进制就是00000011,如果是-3,就是10000011.那么这里的00000011和10000011就是机器数
2.真值:因为第一位是符号位,所以机器数的形式值就不等于真正的数值。例如上面有
符号数10000011,其最高位1代表负,其真正数值是-3而不是形式值131(10000011转换成十进制等于131).所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。
例:00000001的真值为+1,10000001的真值为-1

2.无符号数表示
整个机器字长的全部二进制位均用来表示数值。
例如在八位机中:
10110111B = 183D
11111111B = 255D
如:127转换为二进制为:
假设字长8位:表示: 0111 1111B = 7FH
假设字长16位:表示:0000 0000 0111 1111B = 007FH
3.有符号数表示(负号是1,正号是0)
真值:数值数据的实际值,即带有+、-符号
机器码:用二进制编码表示
机器码的讲解(原反补移)
常用的编码方案有:原码、补码、反补和移码。假定机器数的位数为n+1位,其中一位符号位,其他n位为数值位。
运算器,只有加法运算器,没有减法运算器,所以,计算机中的没法直接做减法的,它的减法是通过加法来实现的。
注意:在机器码中(原反补移)中可以不跟B(二进制)
(1)原码表示法
原码表示法中用最高位表示符号,其中“0”表示正号,“1”表示负号,其他n位表示数值的绝对值,假设机器能处理的位数为8位,即字长为1字节(byte),原码能表示数值的范围是:-127~-0+0~127,共256个。((+0-0是两个数))
符号位:0表示正,1表示负
数值部分:与真值的二进制形式一样
零有两种表示:+0和-0
【+0】原 = 0 0000000 = 00H
【-0】原 = 1 0000000 = 80H
8位定点整数原码的范围是:-127~+127(FFH~7FH)
特点:符号位不是数值的一部分,是人为约定的“0正1负”,所以在运算过程中符号位要单独处理,原码表示法中,数的真值与原码表示间的对应关系简单,相互转换容易,用原码实现乘除的规则简单,缺点是0的编码不唯一,实现加减运算不方便。
如:0001+1001=1010 (1+(-1)=-2)所以原码,虽然直观易懂,易于正值转换。但用来实现加减法的话,运算规则总归是太复杂。于是反码来了。
(2)反码表示法
我们知道,原码最大的问题就在于一个数加上他的相反数不等于零。
例如:0001+1001=1010 (1+(-1)=-2)
于是反码的设计思想就是冲着解决这一点,既然一个负数是一个正数的相反数,那我们干脆用一个正数按位取反来表示负数试试。
正数的反码还是等于原码。负数的反码就是它的原码除符号位,按位取反。是1就变0,是0就变1。假设机器能处理的位数为8位,即字长位1字节(byte),反码能表示数值的范围就为:
-127~-0+0~127,共256个(+0-0是两个数)。
符号位:0表示正,1表示负。
数值部分:正数:与原码相同。 负数:将原码的数值位取反。
零有两种表示: + 0 和 -0
【+0】原 = 0 0000 000
【+0】反 = 0 0000 000
【-0】原 = 1 0000 000
【-0】反 = 1 1111 111
【+5】原 = 0 0000 101
【-5】原 = 1 0000 101
【-5】反 = 1 1111 010
8位定点整数反码的范围是: - 127 ~ + 127
【-127】原 = 1 1111 111
【-127】反 = 1 0000 000
再试着用反码的方式解决一下原码的问题:0001+1110=1111 (1+(-1)= - 0)互为相反数相加等于0,解决。虽然是得到的结果是1111也就是-0。好,我们再试着做一下两个负数相加:1110 + 1100 = 1010((-3)+(-1) = (-5))看来相反数问题是解决了,但是却让两个负数相加的出错了。
(3)补码表示法
注意:只有补码的符号位参与运算。
假设机器能处理的位数为8位,即字长为1字节(byte),补码能表示数值范围为:-128~127,共256个。
正数的补码等于他的原码负数的补码等于反码+1。(这只是一种算补码的方式,多数书对于补码就是这句话)
符号位:0表示正,1表示负
数值部分:正数不变;负数是在反码的基础上末位+1。
【+0】原 = 00H
【+0】反 = 00H
【+0】补 = 00H
【-0】原 = 80H
【-0】反 = FFH
【-0】补 = 00H
补码的特征:
举例:
【-60】原 = 10111100
【-60】反 = 11000011
【-60】补 = 11000100
小结:在8位机中:【-128】原:没有,【-128】反:没有,【-128】补 = 1000000
补码的特点:
补码表示法可以让符号位作为数值的一部分进行参加运算,从而化减法为加法运算,以简化加法器的逻辑设计。在运算器中,加法器是主要的部件,乘除运算也是以加法器为基础,通过增设一些简单的输入逻辑和移位、判别逻辑来实现的,因此补码的应用最为普遍,部分计算机中都采用补码表示法表示数值数据。
(4)移码表示法
移码通常用于表示浮点数的阶码(整数)。
对于正数:符号位为“1”,其余位不变
对于负数:
符号位:1表示正,0表示负。(与前三种相反)
数值部分:与补码数值部分相同
注意:移码与补码的符号位相反,其他位相同。
【X】补求【X】移的规则:数值位不变,符号位求反。
移码的特点:
最高位为符号位,但其取值与前三种编码相反:1代表正,0代表负
在移码表示法中,0有唯一的编码:【+0】移 = 【-0】移 = 1000…00.
移码表示法一般用于表示浮点数的阶码(表示指数大小,有正有负),因此对移码一般只进行
加减运算。
| 机器码 | 原码 | 反码 | 补码 | 移码 |
| 正数 | 符号位:0 其余位同真值 | 同原码 | 同原码 | 符号位变为1 |
| 负数 | 符号位:1 其余位同真值 | 符号位不变,其余各位取反 | 反码+1 | 符号位位0,其余各位取反加1 |
四.机器数的运算--补码加减法
补码加法:
【x+y】补 = 【x】补 + 【y】补
补码减法:
【x-y】补 = 【x】补 + 【-y】补
【y】补 --> 【-y】补:
【y】补-->(包含符号位,各位取反末尾加1)==【-y】补
例如:
x = +1001B(9),y = -0101B(-5),求x+y=?
【x】补 = 01001
【y】补 = 11011

所以:x + y = +0100B = + 4
正数的原反补码一样
五.运算结果溢出的判断。
1.有符号数溢出概念
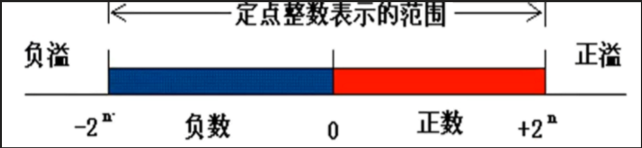
n+1位有符号数补码的范围是:-2^n ~ +2^n-1
8位有符号数补码的范围是:-128~+127(-2^7 ~ +2^7-1)
2.检测方法
两正数加,得负数,为上溢(大于机器所能表示的最大数)
两负数加,得正数,为下溢(小于机器所能表示的最小数)
六.数据的编码
1.ASCII码
标准ASCII码也叫基础ASCII码。
ASCII码使用指定的七位或八位二进制数组合来表示128和256种可能的字符,使用七位二进制数来表示所有的大写和小写字母,数字0到9,标点符号,以及在美式英语种使用的特殊控制字符。(注意:ASCII码与标准ASCII码的位数上的区分,标准ASCII码是七位二进制表示),在电脑中,数字和字母都是用ASCII码来存储的,这就是为什么一个英文字母或半角的数字,标点符号通常占一个字节的原因。
一般用8位来存放一位ASCII码值
用ascii码表示字符需要7位二进制
2.BCD码(Binary coded Decimal)
用4位二进制数表示1位十进制数,这种编码也称为二进制编码表示的十进制数。简称BCD。
非组合(非压缩)BCD码:用一个字节表示一位十进制数
组合(压缩)BCD码:用一个字节表示二位十进制
4位二进制数共有2^4 = 16种组合状态,可选取其中10个编码来表示十进制数的0~9十位数字。
表示10进制数0-9的数字
| 0 | (0000)BCD |
| 1 | (0001)BCD |
| 2 | (0010)BCD |
| 3 | (0011)BCD |
| 4 | (0100)BCD |
| 5 | (0101)BCD |
| 6 | (0110)BCD |
| 7 | (0111)BCD |
| 8 | (1000)BCD |
| 9 | (1001)BCD |
| 59 | (0101 1001)BCD |





![Linux学习[8]查找文件指令:which whereis locate find](https://img-blog.csdnimg.cn/7e39389d51dc4c6fae0e4fbc03b8c3e2.png)




