约瑟夫问题（单向循环链表的使用）

         约瑟夫问题有时也称为约瑟夫斯置换，是一个出现在计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。下面我们将用猴子争大王这一故事以及采用单向循环链表这一方法来进行讲解这一问题。

        设编号为1，2，……n得n个猴子围坐一圈，约定编号为k（k大于等于1并且小于等于n），从1开始报数，数到m的猴子被淘汰。它的下一位继续从1开始报数，数到m的猴子被淘汰，依次类推，最后剩下一个为猴王。

1、根据下图展示，初始化状态：假设n=6，总共有6个人，k=1,从第一个猴开始报数，m=5,每次数五个。

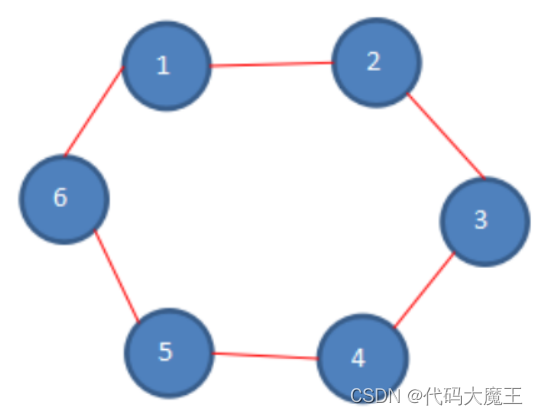
2、第一次报数：从一号开始，数五个数，1-2-3-4-5，数完五个数，五号被淘汰，第一次报数后，剩余猴的数量如下。

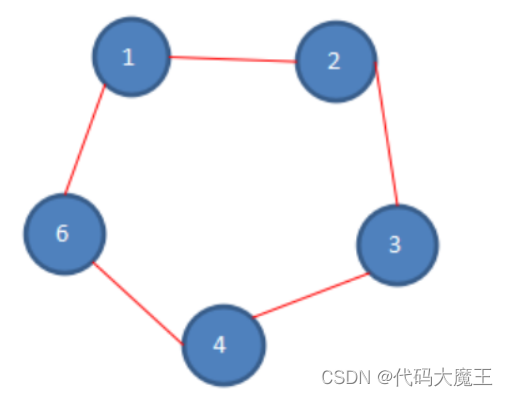
3、第二次报数：从被淘汰的五号的下一位开始报数，也就是六号，数五个数，6-1-2-3-4，数数完毕，四号被淘汰，第二次报数后，剩余猴的数量如下。

4、第三次报数：从被淘汰的四号的下一位开始报数，同样是六号，数五个数，6-1-2-3-6，数数完毕，六号被淘汰，第三次报数后，剩余猴的数量如下。

5、第四次报数：从被淘汰的六号的下一位开始报数，也就是一号，数五个数，1-2-3-1-2，数数完毕，二号被淘汰，第四次报数后，剩余猴的数量如下。

6、第五次报数：从被淘汰的二号的下一位开始报数，也就是三号，数五个数，3-1-3-1-3，数数完毕，三号被淘汰，只剩下一号，那么1号就为猴王。

     

---

       本程序是有关线性表的链式存储结构的应用，通过C语言中提供的结构指针来存储线性表，利用malloc函数动态地分配存储空间。
       约瑟夫环的大小是变化的，因此相应的结点也是变化的，使用链式存储结构可以动态的生成其中的结点，出列操作也非常简单。用单向循环链表模拟其出列顺序比较合适用结构指针描述每个猴：

typedef struct node_t

{

char data;        //数据域

struct node_t *next;     //指针域 ，指针指向自身结构体的类型(存放的下一个节点的地址)

}link_node_t,* link_list_t;   //结构体数据类型，结构体指针类型

struct node_t《-》link_node_t

struct node_t * 《-》link_list_t《-》link_node_t *

解决问题的完整代码如下：

#include <stdio.h>
#include <stdlib.h>
typedef struct node_t
{
    int data;
    struct node_t *next;
}link_node_t,*link_list_t;

int main(int argc, const char *argv[])
{
    link_list_t h=NULL;    //用于指向头结点
    link_list_t pdel=NULL;    //用于指向被删除节点
    link_list_t ptail=NULL;   //用于指向当前链表的尾
    link_list_t pnew=NULL;    //用于指向新创建的节点
    int kill_num;             //数到几淘汰猴子
    int start_num;            //从几号猴子开始
    int all_sum;              //总数
    printf("please input monkey all_sum:");
    scanf("%d",&all_sum);
    printf("please input start_num:");
    scanf("%d",&start_num);
    printf("please input monkey kill_num:");
    scanf("%d",&kill_num);

    h=(link_list_t)malloc(sizeof(link_node_t));
    if(h==NULL)
    {
        printf("error");
        return -1;
    }
    h->data=1;
    h->next=NULL;
    ptail=h;         //尾指针指向当前第一个节点
    for(int i=2;i<=all_sum;i++)
    {

        pnew=(link_list_t)malloc(sizeof(link_node_t));          
        if(pnew==NULL)  //创建新节点
        {
            printf("error");
            return -1;
        }

        pnew->data=i;     //为新节点赋值
        pnew->next=NULL;

        ptail->next=pnew;   //将新节点连接到链表尾部
        ptail=pnew;         //尾指针跟随移动到尾部

    }

    ptail->next=h;           //将头指针保存到链表尾部，形成单向循环链表


    //开始淘汰猴子 
    for(int i=0;i<start_num-1;i++)   //将头指针移动到开始的猴子号码处
        h=h->next;
	//循环进行淘汰猴子
    while(h!=h->next)  //条件不成的时候，就剩一个猴子,只有一个节点  
    {
        for(int i=0;i<kill_num-2;i++)     //将头指针移动到即将删除节点的前一个节点
            h=h->next;

        pdel=h->next;
        h->next=pdel->next;                  //跨过删除节点
        printf("kill %d\n",pdel->data);      //打印被淘汰的猴子
        free(pdel);
        pdel=NULL;
        h=h->next;   //淘汰该猴子后，从下一个节点开始继续开始数,将头指针移动到开始数的地方
    }
    printf("king is %d\n",h->data);         //国王诞生


    return 0;
}
                                                                

运行结果如下：

please input monkey all_sum:6 
please input start_num:1
please input monkey kill_num:5
kill 5
kill 4
kill 6
kill 2
kill 3
king is 1