题目

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

数据范围：数据流中数个数满足 1≤n≤1000，大小满足 1≤val≤1000。

进阶： 空间复杂度 O(n) ， 时间复杂度 O(nlogn)。

示例1

输入：[5,2,3,4,1,6,7,0,8]

返回值："5.00 3.50 3.00 3.50 3.00 3.50 4.00 3.50 4.00 "

说明：数据流里面不断吐出的是5,2,3...,则得到的平均数分别为5,(5+2)/2,3...

示例2

输入：[1,1,1]

返回值："1.00 1.00 1.00 "

---

思路

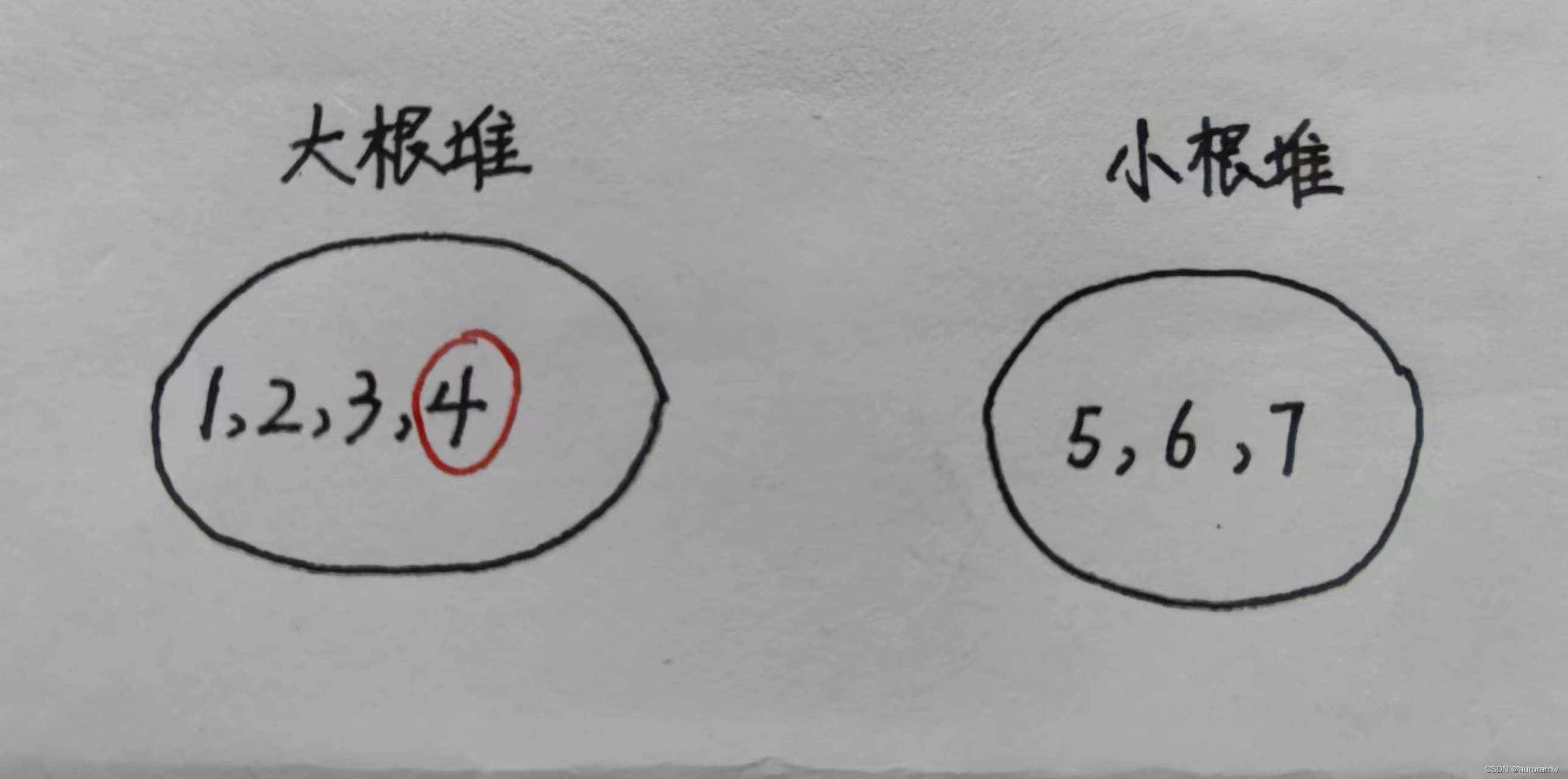
维护两个堆：一个是大根堆：保存较小的那一部分数；一个是小根堆：保存较大的那一部分数。

若n是偶数，它们保存的元素的数目都是n / 2；若n是奇数，大根堆比小根堆多保存一个元素。

要求中位数：

若n是偶数：直接将两个堆的堆顶元素取出，相加除以2即可。

例：[1,2,3,4,5,6]

若n是奇数：(规定大根堆多保存一个元素)直接将大根堆堆顶元素取出即可。

例：[1,2,3,4,5,6,7]

• 时间复杂度：O(1)。
• 空间复杂度：O(n)。

动态维护(插入操作)：

若n是偶数：将要插入的元素添加到小根堆里，再把小根堆堆顶的元素放到大根堆里，这样就进行了动态维护，插入后n为奇数，直接将大根堆堆顶元素取出即可。

若n是奇数：将要插入的元素添加到大根堆里，再把大根堆堆顶的元素放到小根堆里，这样就进行了动态维护，插入后n为偶数，直接将两个堆的堆顶元素取出，相加除以2即可。

• 时间复杂度：O(logn)。
• 空间复杂度：O(n)。

---

代码

import java.util.*;

public class Solution {
    //java使用优先级队列实现大根堆和小根堆，默认是小根堆
    Queue<Integer> min = new PriorityQueue<>();
    Queue<Integer> max = new PriorityQueue<>((x, y) -> (y - x));

    public void Insert(Integer num) {
        if(min.size() == max.size()) { //是偶数
            min.add(num);
            max.add(min.poll());
        } else { //是奇数
            max.add(num);
            min.add(max.poll());
        }
    }

    public Double GetMedian() {
        if(min.size() == max.size()) { //是偶数
            return (min.peek() + max.peek()) / 2.0;
        } else { //是奇数
            return max.peek() * 1.0;
        }
    }
}