Chapter 1 Data Mining

Now, statisticians view data mining as the construction of a statistical model, that is, an underlying distribution from which the visible data is drawn.

However, machine learning can be uncompetitive in situations where we can describe the goals of the mining more directly. Another problem with some machine-learning methods is that they often yield a model that, while it may be quite accurate, is not explainable.

Most other approaches to modeling can be described as either :

Summarizing the data succinctly and approximately, or
Extracting the most prominent features of the data and ignoring the rest.

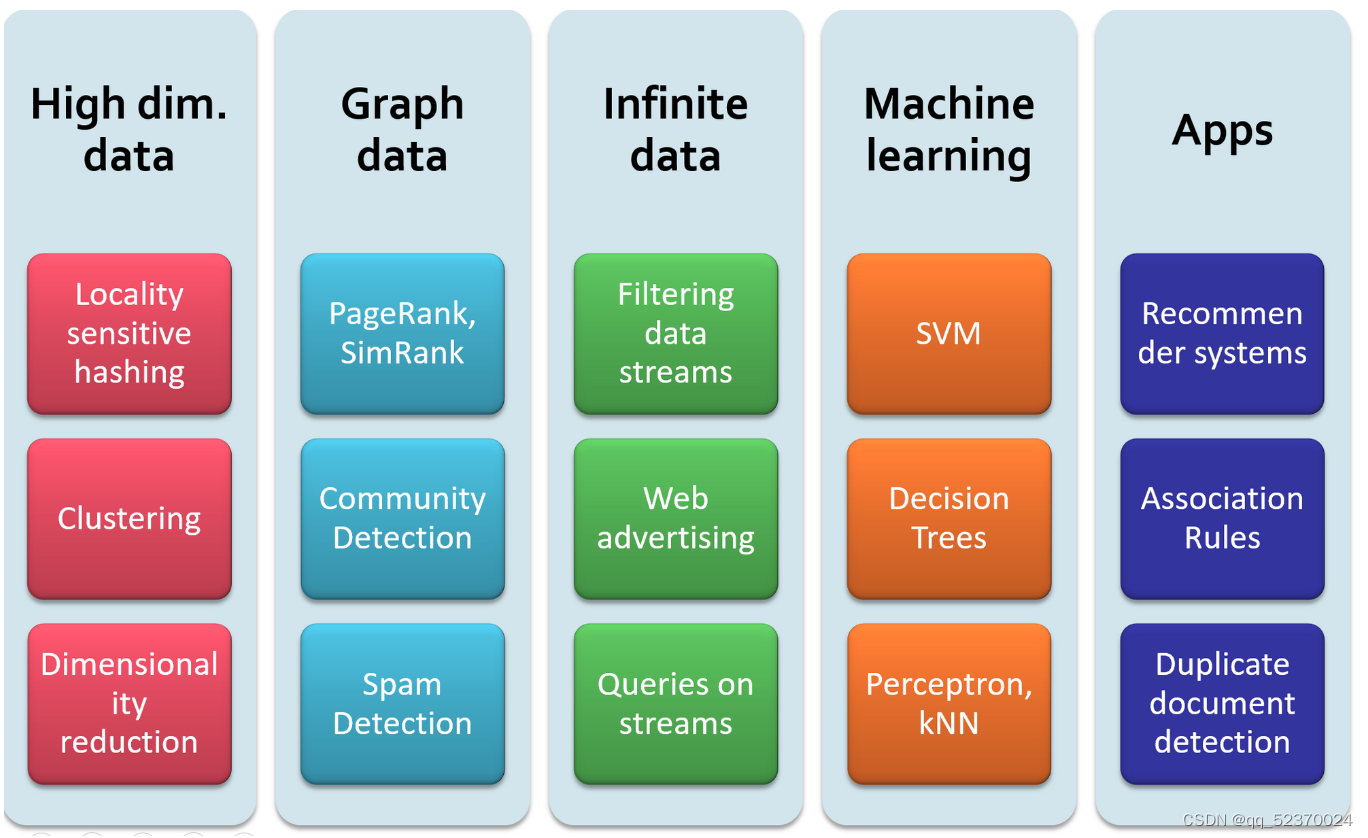
Some of the important kinds of feature extraction from large-scale data that we shall study are:

Frequent Itemsets. This model makes sense for data that consists of “baskets” of small sets of items.
Similar Items. Often, your data looks like a collection of sets, and the objective is to find pairs of sets that have a relatively large fraction of their elements in common.

Suppose you have a certain amount of data, and you look for events of a certain type within that data. You can expect events of this type to occur, even if the data is completely random, and the number of occurrences of these events will grow as the size of the data grows. These occurrences are “bogus,” in the sense that they have no cause other than that random data will always have some number of unusual features that look significant but aren’t.

Bonferroni’s principle, that helps us avoid treating random occurrences as if they were real. Calculate the expected number of occurrences of the events you are looking for, on the assumption that data is random. If this number is significantly larger than the number of real instances you hope to find, then you must expect almost anything you find to be bogus, i.e., a statistical artifact rather than evidence of what you are looking for.

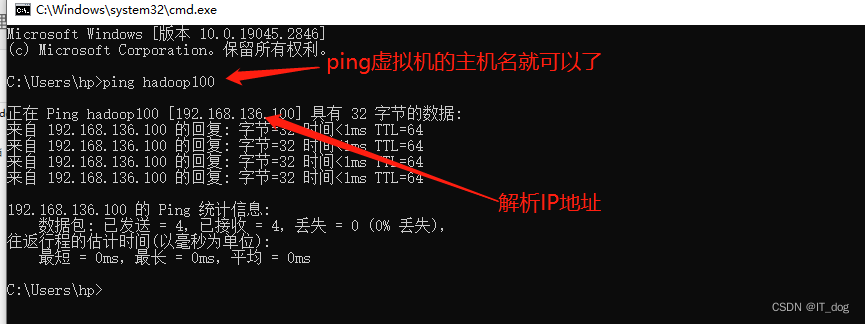
A hash function h takes a hash-key value as an argument and produces
a bucket number as a result. The bucket number is an integer, normally in the range 0 to B − 1, where B is the number of buckets. Hash-keys can be of any type. There is an intuitive property of hash functions that they “randomize” hash-keys. To be precise, if hash-keys are drawn randomly from a reasonable population of possible hash-keys, then h will send approximately equal numbers of hash-keys to each of the B buckets.
在这里插入图片描述

For more complex data types, we can extend the idea used for converting strings to integers, recursively.

For a type that is a record, each of whose components has its own type, recursively convert the value of each component to an integer, using the algorithm appropriate for the type of that component. Sum the integers for the components, and convert the integer sum to buckets by dividing by B.
For a type that is an array, set, or bag of elements of some one type,
convert the values of the elements’ type to integers, sum the integers, and divide by B.

A hash table used as an index; phone numbers are hashed to buckets, and the entire record is placed in the bucket whose number is the hash value of the phone.

Some other useful approximations follow from the Taylor expansion of e:
$e^x=\sum_{i=0}^{\infty}\frac{x^i}{i!}$

There are many phenomena that relate two variables by a power law, that is, a linear relationship between the logarithms of the variables.

Thus, a power law can be written as $y = cx^a$ for some constants $a$ and $c$ .

Often, the existence of power laws with values of the exponent higher than 1 are explained by the Matthew effect. In the biblical Book of Matthew, there is a verse about “the rich get richer.” Many phenomena exhibit this behavior, where getting a high value of some property causes that very property to increase. For example, if a Web page has many links in, then people are more likely to find the page and may choose to link to it from one of their pages as well. As another example, if a book is selling well on Amazon, then it is likely to be advertised when customers go to the Amazon site. Some of these people will choose to buy the book as well, thus increasing the sales of this book.

Summary of Chapter 1

Data Mining: This term refers to applying the powerful tools of computer science to solve problems in science, industry, and many other application areas. Frequently, the key to a successful application is building a model of the data, that is, a summary or relatively succinct representation of the most relevant features of the data.
Bonferroni’s Principle: If we are willing to view as an interesting feature of data something of which many instances can be expected to exist in random data, then we cannot rely on such features being significant. This observation limits our ability to mine data for features that are not sufficiently rare in practice.
TF.IDF: The measure called TF.IDF lets us identify words in a collection of documents that are useful for determining the topic of each document. A word has high TF.IDF score in a document if it appears in relatively few documents, but appears in this one, and when it appears in a document it tends to appear many times.
Hash Functions: A hash function maps hash-keys of some data type to integer bucket numbers. A good hash function distributes the possible hash-key values approximately evenly among buckets. Any data type can be the domain of a hash function.
Indexes: An index is a data structure that allows us to store and retrieve data records efficiently, given the value in one or more of the fields of the record. Hashing is one way to build an index.
Storage on Disk: When data must be stored on disk (secondary memory), it takes very much more time to access a desired data item than if the same data were stored in main memory. When data is large, it is important that algorithms strive to keep needed data in main memory.
Power Laws: Many phenomena obey a law that can be expressed as $y = cx^a$ for some power a, often around −2. Such phenomena include the sales of the x-th most popular book, or the number of in-links to the x-th most popular page.