文章目录
- 【1. 原理】
- 【2. z k z_k zk 所在的路径】
- 【3. CZT的实现步骤】
- 【4. CZT的特点 】
- 【5. CZT的应用】
- 5.1 通过 CZT 变换求 DFT
- 5.2 对信号的频谱进行细化分析
- 5.3 求解Z变换X(z)的零、极点
- 5.4 使用CZT进行Keystone变换
- 【6.相关文献】
- 线性调频Z变换(chirp Z-transform)
【1. 原理】
- Z 变换公式:
X ( z ) = ∑ n = 0 N − 1 x ( n ) z − n X(z)=\sum_{n=0}^{N-1}x(n)z^{-n} X(z)=n=0∑N−1x(n)z−n - 令
z
=
z
k
=
A
W
−
k
=
(
A
0
e
j
θ
0
)
(
W
0
e
−
j
φ
0
)
−
k
=
(
A
0
e
j
θ
0
)
(
W
0
−
k
e
j
φ
0
k
)
,
k
=
0
,
1...
,
M
−
1
z=z_k=AW^{-k}=\left(A_0e^{j\theta_0}\right)\left(W_0e^{-j\varphi_0}\right)^{-k}=\left(A_0e^{j\theta_0}\right)\left(W_0^{-k}e^{j\varphi_0k}\right),k=0,1...,M-1
z=zk=AW−k=(A0ejθ0)(W0e−jφ0)−k=(A0ejθ0)(W0−kejφ0k),k=0,1...,M−1,M代表欲分析的频谱的点数,M不一定等于N。代入上式化简,得到 CZT 变换公式 :
C Z T ( z k ) = ∑ n = 0 N − 1 x ( n ) A − n W n k = ∑ n = 0 N − 1 x ( n ) ( A 0 − n e − j θ 0 n ) ( W 0 n k e − j φ 0 n k ) , k = 0 , 1... , M − 1 \begin{aligned}CZT(z_k)&=\sum_{n=0}^{N-1}x(n)A^{-n}W^{nk}\\&= \sum_{n=0}^{N-1}x(n)\left(A_0^{-n}e^{-j\theta_0n}\right)\left(W_0^{nk}e^{-j\varphi_0nk}\right),k=0,1...,M-1\end{aligned} CZT(zk)=n=0∑N−1x(n)A−nWnk=n=0∑N−1x(n)(A0−ne−jθ0n)(W0nke−jφ0nk),k=0,1...,M−1 - 利用 Bluestein 等式
n
k
=
1
2
[
n
2
+
k
2
−
(
k
−
n
)
2
]
nk=\frac{1}{2}[n^2+k^2-(k-n)^2]
nk=21[n2+k2−(k−n)2],代入上式得:
C Z T ( z k ) = ∑ n = 0 N − 1 x ( n ) A − n W n k = ∑ n = 0 N − 1 x ( n ) A − n W n 2 2 W k 2 2 W − ( k − n ) 2 2 = W k 2 2 ∑ n = 0 N − 1 { [ x ( n ) A − n W n 2 2 ] W − ( k − n ) 2 2 } , k = 0 , 1... , M − 1 \begin{aligned}CZT(z_k)&= \sum_{n=0}^{N-1}x(n)A^{-n}W^{n k}\\ &= \sum_{n=0}^{N-1}x(n)A^{-n}W^{\frac{n^{2}}{2}}W^{\frac{k^{2}}{2}}W^{\frac{-(k-n)^{2}}{2}}\\ &=W^{\frac{k^2}{2}}\sum\limits_{n=0}^{N-1}\{[x(n)A^{-n}W^{\frac{n^2}{2}}]W^{\frac{-(k-n)^2}{2}}\},k=0,1...,M-1\end{aligned} CZT(zk)=n=0∑N−1x(n)A−nWnk=n=0∑N−1x(n)A−nW2n2W2k2W2−(k−n)2=W2k2n=0∑N−1{[x(n)A−nW2n2]W2−(k−n)2},k=0,1...,M−1 - 令
g
(
n
)
=
x
(
n
)
A
−
n
W
n
2
2
,
0
≤
n
≤
N
−
1
,
h
(
n
)
=
W
−
n
2
2
g(n)=x(n)A^{-n}W^{\frac{n^2}{2}},0≤n≤N-1,h(n)=W^{-\frac{n^2}{2}}
g(n)=x(n)A−nW2n2,0≤n≤N−1,h(n)=W−2n2,代入上式,得到:
C Z T ( z k ) = W k 2 2 ∑ n = 0 N − 1 g ( n ) h ( k − n ) , k = 0 , 1... , M − 1 CZT(z_k)=W^{\frac{k^2}{2}}\sum_{n=0}^{N-1}g(n)h(k-n),k=0,1...,M-1 CZT(zk)=W2k2n=0∑N−1g(n)h(k−n),k=0,1...,M−1 - 在上式中,
∑
n
=
0
N
−
1
g
(
n
)
h
(
k
−
n
)
\sum_{n=0}^{N-1}g(n)h(k-n)
∑n=0N−1g(n)h(k−n)是线性卷积,故上式可理解为:
C Z T ( z k ) = W k 2 2 g ( k ) ∗ h ( k ) , k = 0 , 1... , M − 1 CZT(z_k)=W^{\frac{k^2}{2}}g(k)*h(k),k=0,1...,M-1 CZT(zk)=W2k2g(k)∗h(k),k=0,1...,M−1 - 综上所述,CZT 的计算过程可化简为 :

即:让 x(n) 乘 A − n W n 2 2 A^{-n}W^{\frac{n^2}{2}} A−nW2n2 成为 g(n) ,g(n) 再与 h ( n ) = W − n 2 2 h(n)=W^{-\frac{n^2}{2}} h(n)=W−2n2 进行线性卷积,卷积的结果再与 W − k 2 2 W^{-\frac{k^2}{2}} W−2k2 相乘,得到最终CZT变换的结果。 - 总结
C Z T ( z k ) = ∑ n = 0 N − 1 x ( n ) z k − n = ∑ n = 0 N − 1 x ( n ) ( A W − k ) − n = ∑ n = 0 N − 1 x ( n ) ( A 0 − n e − j θ 0 n ) ( W 0 n k e − j φ 0 n k ) , k = 0 , 1... , M − 1 \begin{aligned}CZT(z_k)&=\sum_{n=0}^{N-1}x(n)z_k^{-n}\\&=\sum_{n=0}^{N-1}x(n)(AW^{-k})^{-n}\\&= \sum_{n=0}^{N-1}x(n)\left(A_0^{-n}e^{-j\theta_0n}\right)\left(W_0^{nk}e^{-j\varphi_0nk}\right),k=0,1...,M-1\end{aligned} CZT(zk)=n=0∑N−1x(n)zk−n=n=0∑N−1x(n)(AW−k)−n=n=0∑N−1x(n)(A0−ne−jθ0n)(W0nke−jφ0nk),k=0,1...,M−1
其中, z k = A W − k z_k=AW^{-k} zk=AW−k, A = A 0 e j θ 0 A=A_0e^{j\theta_0} A=A0ejθ0, W = W 0 e − j φ 0 W=W_0e^{-j\varphi_0} W=W0e−jφ0,
z k = A W − k = A 0 W 0 − k e j ( θ 0 + k φ 0 ) \\z_k=AW^{-k}=A_0W_0^{-k}e^{j(\theta_0+k\varphi_0)} zk=AW−k=A0W0−kej(θ0+kφ0),
z 0 = A 0 e j θ 0 , z 1 = A 0 W 0 − 1 e j ( θ 0 + φ 0 ) \\z_0=A_0e^{j\theta_0},\\ z_1=A_0W_0^{-1}e^{j(\theta_0+\varphi_0)} z0=A0ejθ0,z1=A0W0−1ej(θ0+φ0)
z 2 = A 0 W 0 − 2 e j ( θ 0 + 2 φ 0 ) z_2=A_0W_0^{-2}e^{j(\theta_0+2\varphi_0)} z2=A0W0−2ej(θ0+2φ0)
⋯ \cdots ⋯
z M − 1 = A 0 W 0 − ( M − 1 ) e j [ θ 0 + ( M − 1 ) φ 0 ] z_{M-1}=A_0W_0^{-(M-1)}e^{j[\theta_0+(M-1)\varphi_0]} zM−1=A0W0−(M−1)ej[θ0+(M−1)φ0]
【2. z k z_k zk 所在的路径】
-
A
=
A
0
e
j
θ
0
A=A_0e^{j\theta _0}
A=A0ejθ0 为起始点位置。
A 0 A_0 A0 :起始点半径,通常 A 0 ≤ 1 A_0\leq1 A0≤1,表示在圆内, A 0 = 1 A_0=1 A0=1 表示在单位圆上。
θ 0 \theta_0 θ0:起始点相位角,可正可负。 -
z
k
=
A
0
W
0
−
k
e
j
(
θ
0
+
k
φ
0
)
z_k=A_0W_0^{-k}e^{j(\theta_0+k\varphi_0)}
zk=A0W0−kej(θ0+kφ0) 是 z 平面一段螺线上的等分角上某一采样点。
W 0 W_0 W0:螺线的伸展率。
W 0 > 1 W_0>1 W0>1:随 k 的增加螺旋线向内盘旋。
W 0 < 1 W_0<1 W0<1:随 k 的增加螺旋线向外盘旋。
W 0 = 1 W_0=1 W0=1:对应半径为 A 0 A_0 A0 的一段圆弧,若又有 A 0 = 1 A_0=1 A0=1, 则这段圆弧是单位圆的一部分。 -
φ
0
\varphi_0
φ0 是两相邻点之间的角频率差。
φ 0 < 0 \varphi_0<0 φ0<0:表示 z k z_k zk 的路径是顺时针旋转。
φ 0 > 0 \varphi_0>0 φ0>0:表示 z k z_k zk 的路径是逆时针旋转。
【3. CZT的实现步骤】
-
将线性卷积用循环圆卷积进行计算,从而可以变换到频域用FFT进行快速运算。下面为CZT的实现流程图。
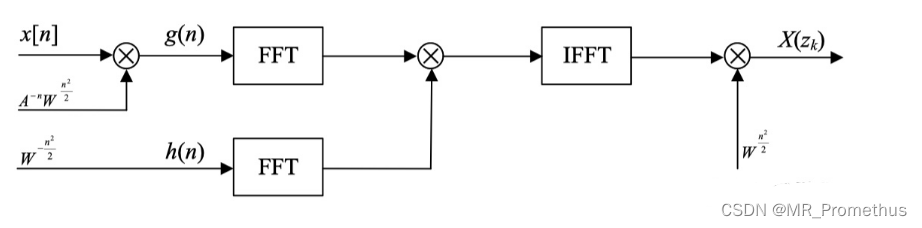
-
选择一个最小数 L,使其满足 L ≥ N + M − 1 L\geq N+M-1 L≥N+M−1,同时又满足 L = 2 m L=2^m L=2m。
-
将 g ( n ) g(n) g(n) 尾补零变成列长为L的序列
g ( n ) = { A − n W n 2 2 x ( n ) 0 ≤ n ≤ N − 1 0 N ≤ n ≤ L − 1 g(n)=\begin{cases}A^{-n}W^{\frac{n^2}{2}}x(n)&0\leq n\leq N-1\\ 0&N\leq n\leq L-1\end{cases} g(n)={A−nW2n2x(n)00≤n≤N−1N≤n≤L−1 -
求 g ( n ) g(n) g(n) 的 FFT
G ( r ) = ∑ n = 0 L − 1 g ( n ) e − j 2 π L n r , 0 ≤ r ≤ L − 1 G(r)=\sum\limits_{n=0}^{L-1}g(n)e^{-j\frac{2\pi}{L}nr},0\leq r \leq L-1 G(r)=n=0∑L−1g(n)e−jL2πnr,0≤r≤L−1 -
h ( n ) h(n) h(n) 补零加长,周期延拓成L点的序列
h ( n ) = { W − n 2 2 0 ≤ n ≤ M − 1 0 M ≤ n ≤ L − N W − ( L − n ) 2 2 L − N + 1 ≤ n ≤ L − 1 h(n)=\left\{\begin{array}{cc}W^{-\frac{n^2}{2}}&0\leq n\leq M-1\\ 0&M\leq n\leq L-N\\ W^{-\frac{(L-n)^2}{2}}&L-N+1\leq n\leq L-1\end{array}\right. h(n)=⎩ ⎨ ⎧W−2n20W−2(L−n)20≤n≤M−1M≤n≤L−NL−N+1≤n≤L−1 -
求 h ( n ) h(n) h(n) 的 FFT
H ( r ) = ∑ n = 0 L − 1 h ( n ) e − j 2 π L n r , 0 ≤ r ≤ L − 1 H(r)=\sum_{n=0}^{L-1}h(n)e^{-j\frac{2\pi}{L}nr},0\leq r \leq L-1 H(r)=n=0∑L−1h(n)e−jL2πnr,0≤r≤L−1 -
求 G ( r ) G(r) G(r) 与 H ( r ) H(r) H(r) 的乘积 Q ( r ) Q(r) Q(r) , Q ( r ) Q(r) Q(r)为 L 点频域离散序列。
Q ( r ) = G ( r ) ⋅ H ( r ) , 0 ≤ r ≤ L − 1 Q(r)=G(r)\cdot H(r),0\leq r \leq L-1 Q(r)=G(r)⋅H(r),0≤r≤L−1 -
求 Q ( r ) Q(r) Q(r) 的 IFFT
q ( r ) = I D F T [ Q ( r ) ] , 0 ≤ n ≤ M − 1 q(r)=IDFT[Q(r)],0\leq n\leq M-1 q(r)=IDFT[Q(r)],0≤n≤M−1 -
最后求出 X ( z k ) X(z_k) X(zk)
X ( z k ) = W − k 2 2 ⋅ q ( k ) , 0 ≤ k ≤ M − 1 X(z_k)=W^{-\frac{k^2}{2}}\cdot q(k),0\leq k\leq M-1 X(zk)=W−2k2⋅q(k),0≤k≤M−1
【4. CZT的特点 】
- 输入序列长N及输出序列长M不需要相等。
- N及M不必是高度合成数,二者均可为素数。
- z k z_k zk 的角间隔是任意的,频率分辨率也是任意的。
- 围线不必是z平面.上的圆,在语音分析中螺旋围线具有某些优点。
- 起始点 z 0 z_0 z0 可任意选定,因此可以从任意频率上开始对输入数据进行窄带高分辨率的分析。
- CZT 是一个一般化的DFT:若 A=1,M=N,可用CZT来计算DFT,即使N为素数时也可以。
【5. CZT的应用】
5.1 通过 CZT 变换求 DFT
- 当满足如下条件时,
z
k
z_k
zk 均匀分布在单位圆上,可由CZT变换求DFT。
1、 M = N M=N M=N
2、 A = A 0 e j θ 0 = 1 ⟹ A 0 = 1 , θ 0 = 0 ∘ A=A_0e^{j\theta_0}=1\Longrightarrow A_0=1,\theta_0=0^\circ A=A0ejθ0=1⟹A0=1,θ0=0∘
3、 W = W 0 e − j φ 0 = e − j 2 π N ⟹ W 0 = 1 , φ 0 = 2 π N W=W_{0}e^{-j\varphi_{0}}=e^{-j\frac{2\pi}{N}}\Longrightarrow W_0=1,\varphi_0=\frac{2\pi}{N} W=W0e−jφ0=e−jN2π⟹W0=1,φ0=N2π - 如果取 A 0 = 1 A_0=1 A0=1, θ 0 \theta_0 θ0为任意值,则所求的DFT是一段任意频率范围的频谱,也就是单位圆上某一段的频谱。这与直接计算DFT求整个频率范围的频谱是不一样的,即使调整N的大小,例如增加N,也只是增加了一段频率范围的计算量而已。
5.2 对信号的频谱进行细化分析
- 其中对窄带信号频谱或对部分感兴趣的频谱进行细化分析。
z
k
z_k
zk 必须在z平面的单位圆上,
A
0
=
1
A_0=1
A0=1,
W
0
=
1
W_0=1
W0=1,即:
z k = A 0 W 0 − k e j ( θ 0 + k φ 0 ) = e j ( θ 0 + k φ 0 ) z_{k}=A_{0}W_{0}^{-k}e^{j(\theta_{0}+k\varphi_{0})}=e^{j(\theta_{0}+k\varphi_{0})} zk=A0W0−kej(θ0+kφ0)=ej(θ0+kφ0)
θ 0 \theta_0 θ0 由感兴趣的起始频率决定。
φ 0 \varphi_0 φ0 由频率分辨率决定。
M 由 φ 0 \varphi_0 φ0 和频率采样的范围决定。
5.3 求解Z变换X(z)的零、极点
- 用于语音信号处理过程中。
- 利用不同半径同心圆,进行等间隔采样,令
W
0
=
1
W_0=1
W0=1,
θ
0
=
0
\theta_0=0
θ0=0,
φ
0
=
2
π
N
\varphi_0=\frac{2\pi}{N}
φ0=N2π,改变
A
0
A_0
A0,计算
20 lg ∣ X ( z k ) ∣ = 20 lg ∣ X ( r e j ω ) ∣ ω = 2 π N k , k = 0 , 1 , . . . N − 1 20\operatorname{lg}|X(z_k)|=20\operatorname{lg}|X(re^{j\omega})|_{\omega=\frac{2\pi}{N}k},k=0,1,...N-1 20lg∣X(zk)∣=20lg∣X(rejω)∣ω=N2πk,k=0,1,...N−1
其中, 20 lg ∣ X ( r e j w ) ∣ ( d B ) 20\lg|X(re^{jw})|(dB) 20lg∣X(rejw)∣(dB)的峰值决定 X(z) 的极点,谷值决定零点。
5.4 使用CZT进行Keystone变换
- 令
A
=
1
,
W
=
e
−
j
f
0
+
f
f
0
2
π
M
A=1,W=e^{-j\frac{f_0+f}{f_0}\frac{2\pi}{M}}
A=1,W=e−jf0f0+fM2π ,即
N = M A 0 = W 0 = 1 θ 0 = 0 ϕ 0 = f 0 + f f 0 2 π M \begin{array}{l}N=M\\ A_0=W_0=1\\ \theta_0=0\\ \phi_0=\frac{f_0+f}{f_0}\frac{2\pi}{M}\end{array} N=MA0=W0=1θ0=0ϕ0=f0f0+fM2π
然后按照CZT的计算步骤进行计算。使用此方法可以大大减小Keystone变换的计算量。
【6.相关文献】
线性调频Z变换
Keystone学习笔记(5)——Keystone变换的实现方法