一. 区间DP简单介绍

二. 区间DP模板

三. 区间DP经典案例

1.leetcode1312 让字符串成为回文串的最少插入次数

2.leetcode1039 多边形三角剖分的最低得分

以上部分，见

区间DP (Java) 解析/模板/案例

3.leetcode1547 切棍子的最小成本

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

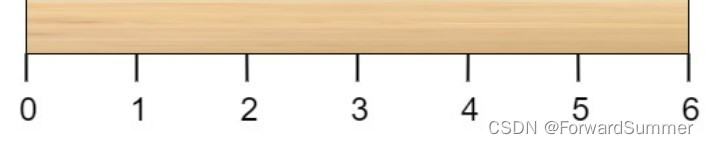
给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的最小总成本。

输入：n = 7, cuts = [1,3,4,5]
输出：16
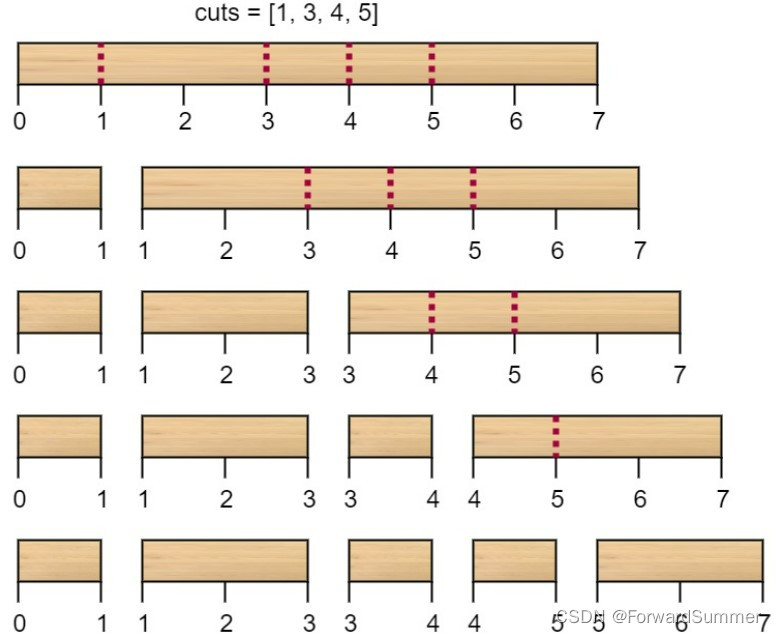
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：
第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
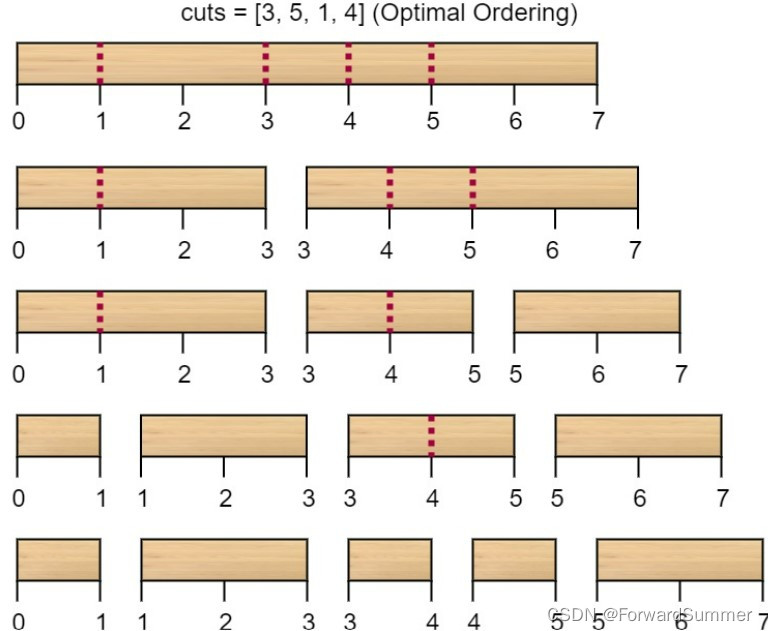
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

class Solution {
    public int minCost(int n, int[] cuts) {
        Arrays.sort(cuts);
        int len = cuts.length;
        int[] cutsSE = new int[len+2];
        cutsSE[len+1] = n;
        for(int i = 0; i < len; i++){
            cutsSE[i+1] = cuts[i]; 
        }
        int lenSE = cutsSE.length;
        int[][] dp = new int[lenSE][lenSE];
        for(int i = lenSE-2; i >= 0; i--){
            for(int j = i+2; j < lenSE; j++){
                dp[i][j] = 0x3f3f3f3f;
                for(int k = i+1; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k][j]+(cutsSE[j]-cutsSE[i]));
                }
            }
        }
        return dp[0][lenSE-1];
    }
}

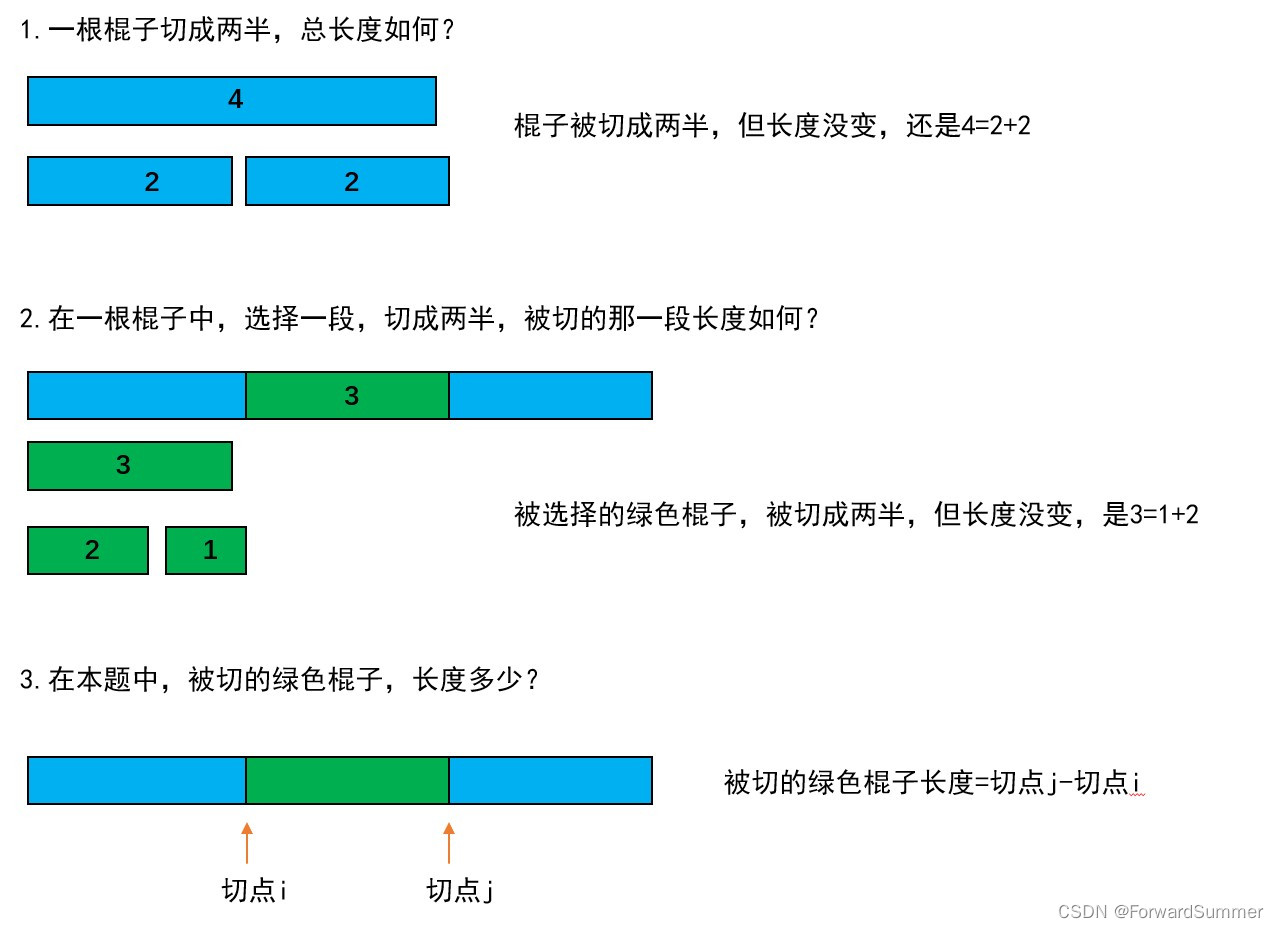
此题和第2题 leetcode1039 多边形三角剖分的最低得分一样，也是可以枚举切点。对于区间DP的一大部分题目，都是可以枚举左右切点，不必枚举长度，枚举左右端点其实也相当于枚举长度。

4.leetcode375 猜数字大小 II

我们正在玩一个猜数游戏，游戏规则如下：

我从 1 到 n 之间选择一个数字。
你来猜我选了哪个数字。
如果你猜到正确的数字，就会赢得游戏。
如果你猜错了，那么我会告诉你，我选的数字比你的更大或者更小，并且你需要继续猜数。
每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会输掉游戏。
给你一个特定的数字 n ，返回能够确保你获胜的最小现金数，不管我选择那个数字。

输入：n = 10
输出：16
解释：制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
        - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
        - 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
        - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
            - 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
            - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
        - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
            - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

class Solution {
    public int getMoneyAmount(int n) {
        int[][] dp = new int[n+1][n+1];
        for(int i = n-1; i >= 1; i--){
            for(int j = i+1; j <= n; j++){
                dp[i][j] = 0x3f3f3f3f;
                for(int k = i; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j],Math.max(dp[i][k-1],dp[k+1][j])+k);
                }
            }
        }
        return dp[1][n];
    }  
}

本题小结：

（1）由于题目要求是从 1 到 n 之间选择一个数字，所以dp数组最后返回的范围也是 dp[1][n]

（2）对应数组的长度被设置成int[n+1][n+1]

（3）i的枚举顺序从大到小，这和前几题的原因是一样的，不再赘述

（4）本题最难的部分，为min函数中的max函数，即在选择k的左右子区间选择大的值

（5）考虑到最坏的情况，所以在k的左右两边取大值，而题目要求最小现金数，明显在外层是min函数

5.leetcode1000 合并石头的最低成本

有 N 堆石头排成一排，第 i 堆中有 stones[i] 块石头。

每次移动（move）需要将连续的 K 堆石头合并为一堆，而这个移动的成本为这 K 堆石头的总数。

找出把所有石头合并成一堆的最低成本。如果不可能，返回 -1 。

输入：stones = [3,2,4,1], K = 2
输出：20
解释：
从 [3, 2, 4, 1] 开始。
合并 [3, 2]，成本为 5，剩下 [5, 4, 1]。
合并 [4, 1]，成本为 5，剩下 [5, 5]。
合并 [5, 5]，成本为 10，剩下 [10]。
总成本 20，这是可能的最小值。

输入：stones = [3,2,4,1], K = 3
输出：-1
解释：任何合并操作后，都会剩下 2 堆，我们无法再进行合并。所以这项任务是不可能完成的。.

class Solution {
    public int mergeStones(int[] stones, int k) {
        int len = stones.length;
        if((len-1) % (k-1) > 0) return -1;
        int[][] dp = new int[len][len];
        int[] pre = new int[len+1]; 
        for(int i = 0; i < len; i++){
            pre[i+1] = pre[i]+ stones[i];
        }
        for(int i = len-1; i >=0; i--){
            for(int j = i+1; j < len; j++){
                dp[i][j] = 0x3f3f3f3f;
                for(int x = i; x < j; x += k-1){
                    dp[i][j] = Math.min(dp[i][j], dp[i][x]+dp[x+1][j]);
                }
                if((j-i) % (k-1) == 0){
                    dp[i][j] += pre[j+1] - pre[i];
                }
            }
        }
        return dp[0][len-1];
    }
}

本题小结：

（1）假设长度为n，最后变为1堆，那么较少的数量为n-1个，每次把k个合并为一个，减少的部分为k-1个，当(len-1) % (k-1) > 0 证明不能合并为一堆

（2）i为倒叙，j为正序，根据以上四题，情况相似，不再赘述

（3）x可看作切点，当从x切开，左右两边之和将构成整体，然后取整体最小情况

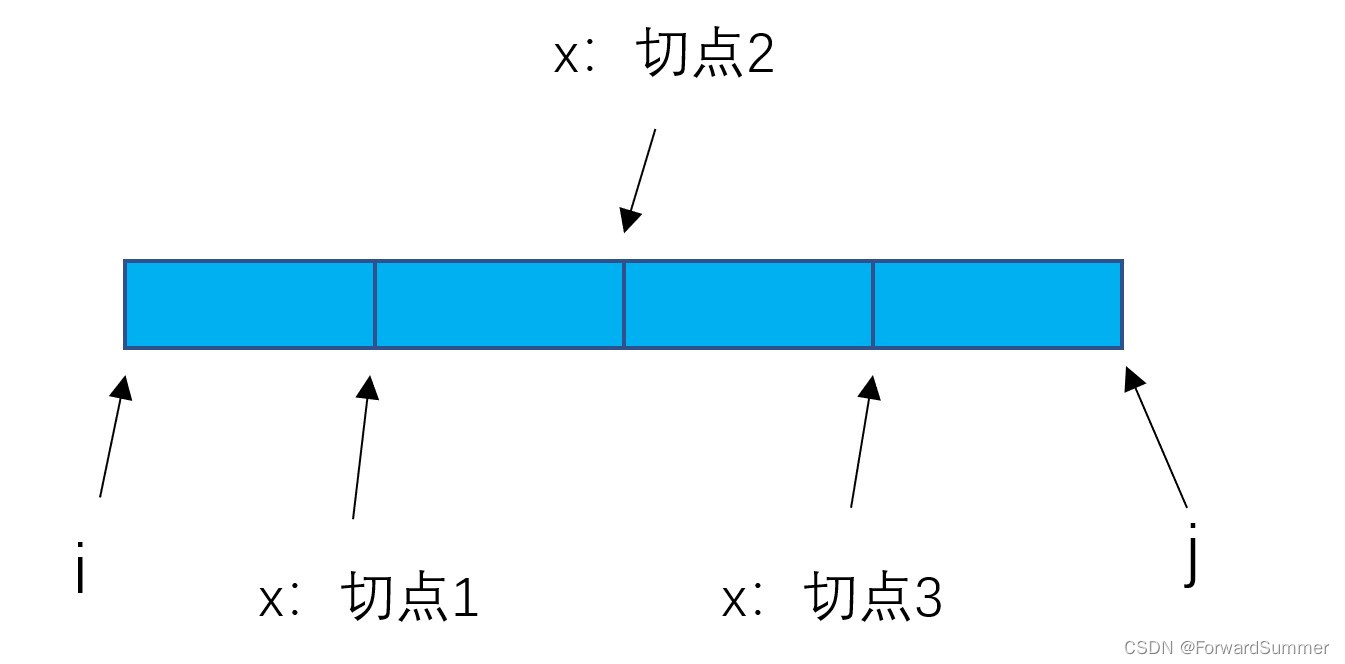
（4）左起i，右到j，如果(j-i) % (k-1) > 0则证明不能最后合并为一堆

（5）因为需要用到区间之和，所以需要使用前缀和

当案例为[3,2,4,1], k = 2时

我们合并3和2，那么可得到

[5,4,1]，此时的和为5，也就是从3到2区间长度为2的区间之和

那么合并5和4，那么可得到

[9,1]，此时的和为5+9，此轮花费为9，也就是从3到4区间长度为3的区间之和，一共花费为14

那么再进行合并，得到最后的结果，我们可知道，每轮的花费都是区间之和

最后的答案是选择的区间之和的和

那么区间之和可使用前缀和来处理