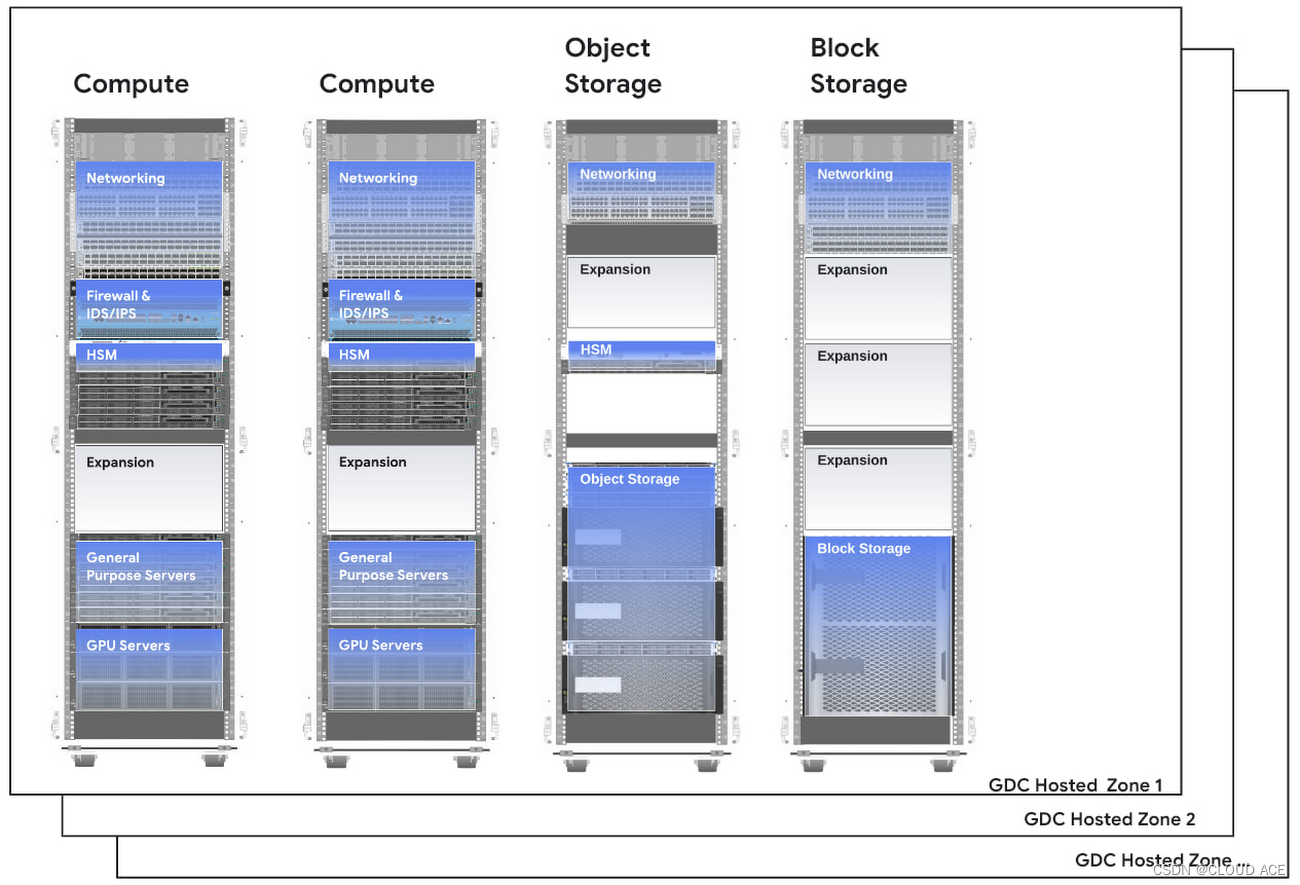
平衡二叉树是子啊二叉排序树的基础上建立的,他的概念就是这棵树中的任意节点的平衡因子都必须要大于1或是小于-1。平衡因子就是这个节点的左子树高度减右子树高度所得到的差。那么,它有什么优点呢?为什要在二叉排序树的基础上来建立这个平衡二叉树呢?我们来看下面的这幅图:

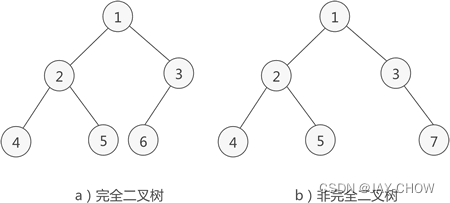
在这个二叉排序树中,如果要查一个节点的数据域,那么它的时间复杂度是多少呢?我们知道,在学时间复杂度的时候,我们一般都是根据最坏的结果来计算的,那么,它的最差的时间复杂度用大O表法,是不是就是O(n),但是如果这是一个平衡二叉树的话,那么,这个平衡二叉树的搜索时间就是O(log n)。为什么呢?我们可以看下面的这幅图:
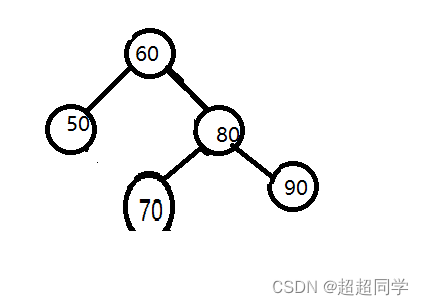
如果是平衡二叉树的话,这个树就会是这个样子。是不是就会很容易的找到了呢?这里有关于旋转,下面会说。这个就是关于平衡二叉树的好处。那么,还是老样子,究竟该怎么样实现他呢?接下来就来代码实现了:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef struct tree
{
int val;
struct tree* left;
struct tree* right;
}tree;
void push(tree** root, int x);
void adjust(tree** root, int x);
tree* find(tree* root, int x);
void print(tree* root);#define _CRT_SECURE_NO_WARNINGS 1
#include"tree.h"
void push(tree** root, int x)
{
assert(root);
if (*root == NULL)
{
tree* new = (tree*)malloc(sizeof(tree));
assert(new);
new->left = NULL;
new->right = NULL;
new->val = x;
*root = new;
}
else
{
if (x < (*root)->val)
push(&(*root)->left, x);
else
push(&(*root)->right, x);
}
}
static int high(tree* root)
{
if (root == NULL)
return 0;
else
{
int left = high(root->left);
int right = high(root->right);
if (left >= right)
return left + 1;
else
return right + 1;
}
}
void adjust(tree** root, int x)
{
assert(root);
if (*root == NULL)
return;
else
{
int left = high((*root)->left);
int right = high((*root)->right);
int balance = left - right;
//不平衡就旋转最小不平衡的子树
if (balance > 1 || balance < -1)
{
if (x < (*root)->val)
{
//LL
if (x < (*root)->left->val)
{
tree* cur = (*root)->left->right;
tree* tem = (*root)->left;
tem->right = *root;
*root = tem;
(*root)->right->left = cur;
}
else
{
//LR
tree* cur = (*root)->left->right;
tree* tem = (*root)->left;
tree* last = cur->left;
cur->left = tem;
tem->right = last;
(*root)->left = cur;
tem = cur->right;
cur->right = *root;
last = cur->right;
last->left = tem;
*root = cur;
}
}
else
{
if (x > (*root)->right->val)
{
//RR型
tree* cur = (*root)->right;
tree* tem = (*root)->right->left;
cur->left = *root;
*root = cur;
(*root)->left->right = tem;
}
else
{
//RL型
tree* cur = (*root)->right->left;
tree* tem = (*root)->right;
tree* last = cur->right;
cur->right = tem;
tem = cur->right;
tem->left = last;
(*root)->right = cur;
last = cur->left;
cur->left = *root;
*root = cur;
(*root)->left->right = last;
}
}
}
//平衡就继续遍历他的左右子树
else
{
adjust(&(*root)->left, x);
adjust(&(*root)->right, x);
}
}
}
tree* find(tree* root, int x)
{
if (root == NULL)
return NULL;
if (x == root->val)
return root;
else
{
find(root->left, x);
find(root->right, x);
}
}
void print(tree* root)
{
if (root == NULL)
return;
else
{
print(root->left);
printf("%d->", root->val);
print(root->right);
}
}#define _CRT_SECURE_NO_WARNINGS 1
#include "tree.h"
void test()
{
tree* root = NULL;
push(&root, 50);
//adjust(&root, 50);
push(&root, 55);
//adjust(&root, 55);
push(&root, 54);
//adjust(&root, 54);
push(&root, 46);
//adjust(&root, 46);
push(&root, 41);
//adjust(&root, 41);
push(&root, 48);
//adjust(&root, 48);
push(&root, 59);
//adjust(&root, 59);
push(&root, 60);
//adjust(&root, 60);
push(&root, 70);
tree* ret = find(root, 59);
tree* tem = find(root, 55);
adjust(&ret, 70);
tem->right = ret;
print(root);
}
int main()
{
test();
return 0;
}以上是我实现的代码,大体思想就是先按照普通的二叉排序树来建立一颗树,然后在检查不平衡的子树,然后再旋转。
旋转有四种情况:1.LL:就是插入的节点在当前节点的左子树的左孩子处,然后此时的思想就是旋转,此时的这个节点就是最小不平衡子树,我们把他的左孩子旋转,类似于下图:
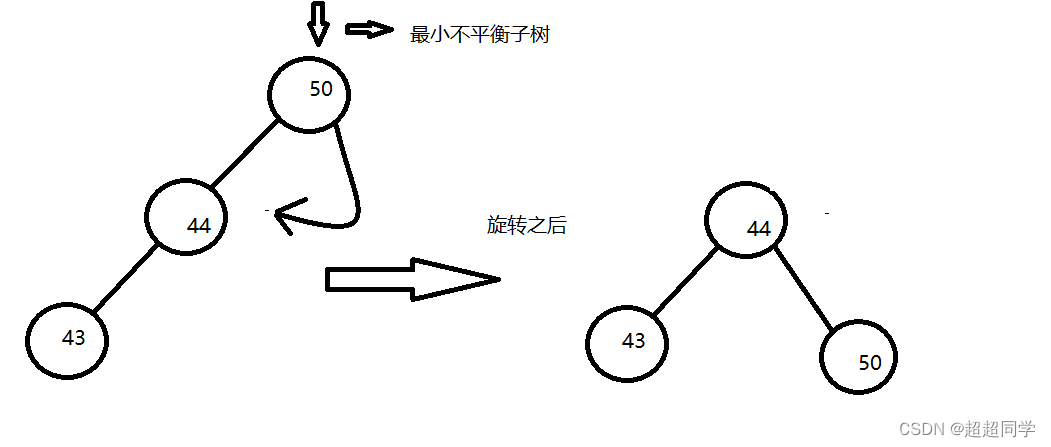
就是这样,如果当前节点的左孩子有右子树,那么就要把他的右子树插入到旋转之后的左子树处,按照上图来说就是把44的右子树插入到旋转之后的50的左子树处。
2.RR:这个和LL型原理一样,就是旋转的方向不同而已,此时要注意,这里就不再多说。
3.LR:这个就是要把当前节点的左孩子的右孩子旋转到根节点的位置,具体如下图:
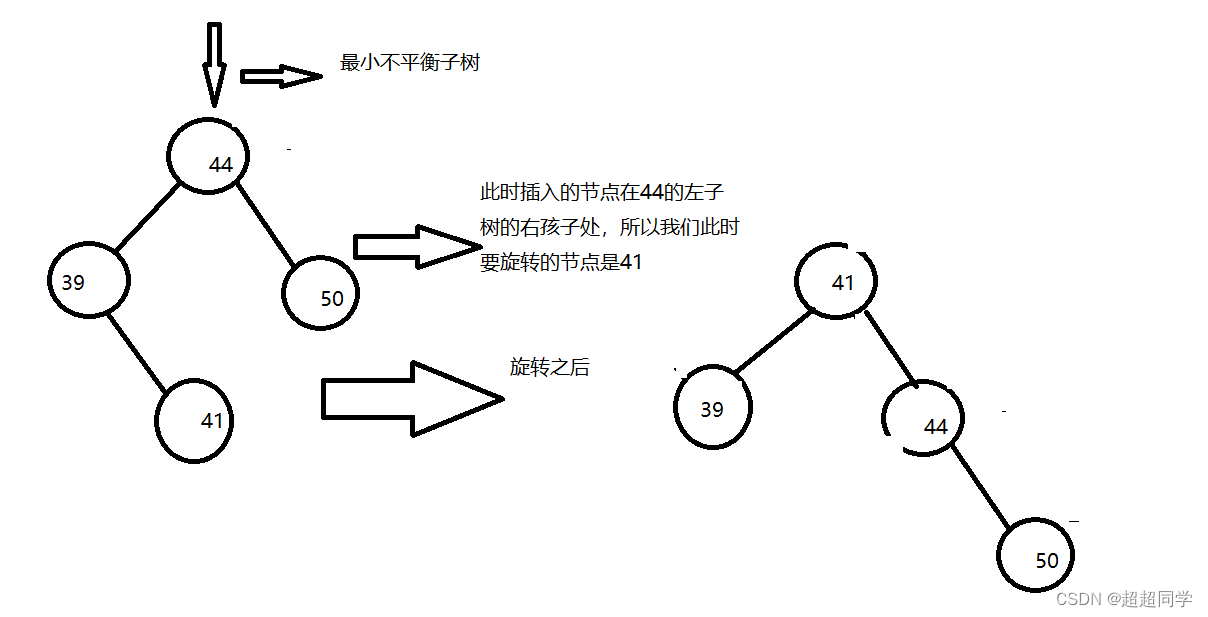
注意的是旋转的节点如果有左子树或是右子树,我们应该提前保存它,旋转之后在插入。
4.RL:这个和LR一样,也就是旋转的方向不同,思路是一样的。
好了,旋转的思想给大家说完,那么就是代码了,上面的代码是调试的时候可以清楚的看到,但是唯一不好的地方在于必须提前把最小不平衡子树找到,然后传入不平衡节点的地址,还有找到他的前驱,以方便旋转完成之后继续衔接。
最后,希望大家可以支持一下,谢谢!!!