1.问题

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1

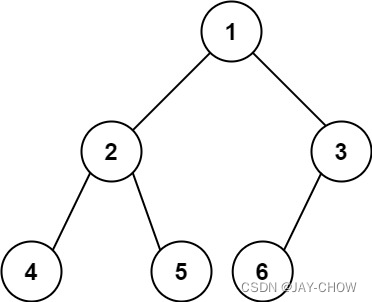
在这里插入图片描述

输入：root = [1,2,3,4,5,6]
输出：6

示例 2

输入：root = []
输出：0

示例 3

输入：root = [1]
输出：1

提示：

树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是完全二叉树

2.解题思路

2.1 递归

二叉树节点个数通用公式可以总结为：左子树节点数+右子树节点数+1，因而利用递归可以非常快的写出代码：

countNodes(TreeNode root){
	//空节点，节点个数为0
	if root为空节点
		return 0;
	return countNodes(root.left) + countNodes(root.right) + 1;
}

2.2 广度优先

2.2.1 满二叉树

《数据结构》严蔚敏、吴伟民一书中对于满二叉树具有详细的定义，即一颗深度为k且具有2^k-1个节点的二叉树称之为满二叉树。比如：
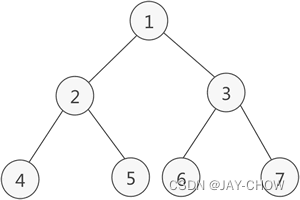
在这里插入图片描述

2.2.2 完全二叉树

假设对满二叉树的节点进行连续编号，约定编号从根节点开始，自上而下，自左至右。对于深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中编号从1至n的节点一一对应，称之为完全二叉树。比如：
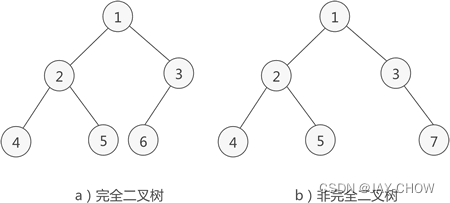
在这里插入图片描述
若root为编号k(k>=1)，在完全二叉树中，若root只有左节点，其编号应为2k，若有右节点，则编号为2k+1。

层序遍历直到遇到第一个左子树为空的节点，若编号为k，则节点总数为2k-1，或直到遇到第一个右子树为空的节点，节点总数2k。（参考：102.二叉树的层序遍历）

3.代码

3.1 递归

public int countNodes(TreeNode root) {
    if(null==root){
        return 0;
    }
    int leftNodes=countNodes(root.left);
    int rightNodes=countNodes(root.right);
    return leftNodes + rightNodes + 1;
}

3.2 广度优先

public int countNodes(TreeNode root) {
    if(null==root){
        return 0;
    }
    //队列
    Queue<TreeNode> q=new LinkedList<>();
    //临时节点
    TreeNode tmp;
    //入队
    q.offer(root);
    //编号
    int code=0;
    //结果
    int res=0;

    while(!q.isEmpty()){
        tmp=q.poll();
        //编号加1
        code++;
        //如果左节点为空，结束遍历
        if(null==tmp.left){
            res=2*code-1;
            break;
        }
        //否则，加入队列，继续遍历
        else {
            q.offer(tmp.left);
        }
        if(null==tmp.right){
            res=2*code;
            break;
        }
        else {
            q.offer(tmp.right);
        }
    }
    return res;
}