目录
一、主成分分析
1.princomp命令
2.screeplot命令
3.【例7.3.3】对【例6.3.3】中的数据从相关矩阵出发进行主成分分析
编辑(1)代码
(2)碎石图
(3)散点图
二、因子分析
1.载荷矩阵求解
(1)主成分法
(2)主因子法
(3)极大似然法
2.【例8.3.1】
(1)因子载荷图
(2)因子得分散点图
(3)其他结果
一、主成分分析
1.princomp命令
princomp(x,cor=FALSE,scores=TRUE,...)
x 数据矩阵或数据框
cor 是否用相关阵,默认为协方差矩阵(0-1变量)
scores 是否输出成分得分(默认输出,0-1变量)
2.screeplot命令
screeplot(x,npcs=min(10,length(x$sdev)),type=c("barplot","lines"),...)
x 主成分分析对象,由princomp()或prcomp()产生的结果
npcs 主成分个数
type 图形类型
3.【例7.3.3】对【例6.3.3】中的数据从相关矩阵出发进行主成分分析

(1)代码
> d7.3.3=read.csv('D:/个人成长/学业/课程/应用多元统计分析/上机/上机四/examp7.3.3.csv',header=1)
> data=d7.3.3[,3:10]#去除前两列
> rownames(data)=d7.3.3[,1]#用第一列命名
> princ=princomp(data,cor=1,scores=1)
> summary(princ,loadings = 1)#显示载荷
Importance of components:
Comp.1 Comp.2 Comp.3
Standard deviation 2.2578087 1.1628692 0.75810535
Proportion of Variance 0.6372125 0.1690331 0.07184047
Cumulative Proportion 0.6372125 0.8062456 0.87808609
Comp.4 Comp.5 Comp.6
Standard deviation 0.63740988 0.5303471 0.3496810
Proportion of Variance 0.05078642 0.0351585 0.0152846
Cumulative Proportion 0.92887251 0.9640310 0.9793156
Comp.7 Comp.8
Standard deviation 0.30443012 0.269809906
Proportion of Variance 0.01158471 0.009099673
Cumulative Proportion 0.99090033 1.000000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
x1 0.401 0.415 0.209 0.221 0.750
x2 0.132 -0.749 0.332 0.152 -0.529
x3 0.375 -0.442 0.547 -0.559 0.181 -0.105
x4 0.320 -0.345 -0.478 -0.659 0.309
x5 0.388 0.232 0.279 -0.366 -0.214 -0.103 0.673 -0.273
x6 0.406 -0.310 0.233 0.806 -0.163
x7 0.326 0.496 -0.580 -0.548
x8 0.396 0.345 -0.107 0.529 -0.435 -0.476
> princ$scores
Comp.1 Comp.2 Comp.3 Comp.4
北京 5.5161422 -2.50738325 -0.77237661 -0.342025615
天津 2.0395681 -0.04563995 -0.83615394 0.845550297
河北 -0.7822984 -0.59008148 -0.65966138 -0.410902847
山西 -1.8792813 -0.41113554 -0.05723669 -0.086036840
内蒙古 -1.8569219 -0.51833926 0.12885672 -0.102232535
辽宁 -1.3352690 -0.85879963 -0.07295730 -0.576044895
吉林 -1.8905078 -0.15386110 -0.04046477 -0.296049069
黑龙江 -1.9594375 -0.64721626 -0.28170233 -0.862687274
上海 5.9635549 0.19882326 0.11788332 1.085848268
江苏 0.4139376 0.31711635 -0.21365686 0.861545735
浙江 3.6431786 -0.54063248 -0.78646972 -0.684308990
安徽 -1.8264346 0.52788853 0.33100537 0.642538363
福建 0.2044823 1.35964846 1.30111197 0.231632889
江西 -2.2713675 1.89803737 0.07386560 0.332878628
山东 -0.1499016 -1.00010576 -0.36632612 0.913937191
河南 -1.9794541 0.39454008 -0.21711881 -0.244562530
湖北 -0.7288631 0.25132273 -0.05482822 0.277902017
湖南 0.2226418 0.20691787 -0.02909273 0.470176015
广东 5.6758378 3.12277958 0.52172837 -1.529260906
广西 -0.2557057 2.09250406 -0.03651883 0.291080570
海南 -1.1766527 1.94469519 0.46155090 -0.589557379
重庆 1.1340597 -0.41674742 0.12704843 0.629589843
四川 -0.5424717 -0.04247969 0.16290535 0.419172390
贵州 -1.3196061 0.34762932 -0.12312120 0.817252337
云南 0.4429362 -0.48701392 0.64894716 -0.040703432
西藏 0.4445469 -2.40409300 3.23404939 -0.229531640
陕西 -0.8736815 0.50934383 -1.11617814 -0.074288401
甘肃 -1.5750355 -0.53491812 -0.12108276 -0.002785615
青海 -1.0624690 -0.43313740 -0.35904397 -0.952612580
宁夏 -1.5265344 -0.92190271 -0.60200671 -1.089744116
新疆 -0.7089928 -0.65775971 -0.36295547 0.294230122
Comp.5 Comp.6 Comp.7 Comp.8
北京 0.49015165 0.743102047 -0.098562113 -0.08910465
天津 0.24328663 -0.377477580 -0.549501112 0.24650248
河北 -0.32670023 0.016344427 0.122855971 -0.07702872
山西 0.28489684 -0.137369274 -0.136499613 -0.28718747
内蒙古 -0.20860949 0.163852588 0.164486223 -0.52223829
辽宁 -0.42650567 0.059648378 0.030704280 0.54582578
吉林 -0.45184342 0.344488301 -0.043751175 0.28055969
黑龙江 -0.36880302 -0.112321327 -0.026196541 0.31085892
上海 0.59982359 -0.097601868 -0.135026990 0.26296022
江苏 0.38534626 -0.433403877 0.178460160 0.04519613
浙江 -0.17462701 -0.442334468 0.429224299 0.27201373
安徽 0.02958280 0.480614865 0.518568486 0.16334095
福建 -0.12425350 -0.239464085 0.307083675 0.67352652
江西 -0.10059999 0.013674833 -0.423435094 -0.01167376
山东 -0.54786040 -0.277350502 0.240509108 -0.41656008
河南 -0.30250577 -0.500718492 -0.289019565 0.07335934
湖北 -0.82549379 0.663110050 -0.476650840 0.10559611
湖南 -0.48303746 0.544463634 0.022265459 -0.23687135
广东 -0.89608022 -0.187865971 0.009515989 -0.46318481
广西 0.04433797 0.451971755 -0.123006372 -0.04628156
海南 1.85647105 0.348116693 0.327398414 -0.07905539
重庆 -0.58007045 0.272363853 0.741611104 0.02525413
四川 -0.13493483 0.304817301 -0.294712518 0.11965937
贵州 0.15167210 -0.517812319 0.342293577 -0.24195384
云南 0.51148937 -0.001527241 -0.513698867 -0.14685737
西藏 -0.06677950 -0.318751852 -0.208326108 -0.12111402
陕西 -0.03786457 -0.452909680 -0.300494085 -0.05480253
甘肃 0.57694558 -0.113304293 -0.023866750 -0.24677592
青海 0.66397194 0.100058941 -0.106167454 0.13235921
宁夏 0.33346104 -0.158692833 0.246421912 0.04069613
新疆 -0.11486753 -0.137722003 0.067516541 -0.25701892
> screeplot(princ,type='l')#碎石土,用线连接
> score=princ$scores[,1:2]#取出一二主成分得分
Warning messages:
1: In doTryCatch(return(expr), name, parentenv, handler) :
display list redraw incomplete
2: In doTryCatch(return(expr), name, parentenv, handler) :
invalid graphics state
3: In doTryCatch(return(expr), name, parentenv, handler) :
invalid graphics state
> score[order(score[,'Comp.1']),]#按第一主成分得分排序
Comp.1 Comp.2
江西 -2.2713675 1.89803737
河南 -1.9794541 0.39454008
黑龙江 -1.9594375 -0.64721626
吉林 -1.8905078 -0.15386110
山西 -1.8792813 -0.41113554
内蒙古 -1.8569219 -0.51833926
安徽 -1.8264346 0.52788853
甘肃 -1.5750355 -0.53491812
宁夏 -1.5265344 -0.92190271
辽宁 -1.3352690 -0.85879963
贵州 -1.3196061 0.34762932
海南 -1.1766527 1.94469519
青海 -1.0624690 -0.43313740
陕西 -0.8736815 0.50934383
河北 -0.7822984 -0.59008148
湖北 -0.7288631 0.25132273
新疆 -0.7089928 -0.65775971
四川 -0.5424717 -0.04247969
广西 -0.2557057 2.09250406
山东 -0.1499016 -1.00010576
福建 0.2044823 1.35964846
湖南 0.2226418 0.20691787
江苏 0.4139376 0.31711635
云南 0.4429362 -0.48701392
西藏 0.4445469 -2.40409300
重庆 1.1340597 -0.41674742
天津 2.0395681 -0.04563995
浙江 3.6431786 -0.54063248
北京 5.5161422 -2.50738325
广东 5.6758378 3.12277958
上海 5.9635549 0.19882326
> score[order(score[,'Comp.2']),]#按第二主成分得分排序
Comp.1 Comp.2
北京 5.5161422 -2.50738325
西藏 0.4445469 -2.40409300
山东 -0.1499016 -1.00010576
宁夏 -1.5265344 -0.92190271
辽宁 -1.3352690 -0.85879963
新疆 -0.7089928 -0.65775971
黑龙江 -1.9594375 -0.64721626
河北 -0.7822984 -0.59008148
浙江 3.6431786 -0.54063248
甘肃 -1.5750355 -0.53491812
内蒙古 -1.8569219 -0.51833926
云南 0.4429362 -0.48701392
青海 -1.0624690 -0.43313740
重庆 1.1340597 -0.41674742
山西 -1.8792813 -0.41113554
吉林 -1.8905078 -0.15386110
天津 2.0395681 -0.04563995
四川 -0.5424717 -0.04247969
上海 5.9635549 0.19882326
湖南 0.2226418 0.20691787
湖北 -0.7288631 0.25132273
江苏 0.4139376 0.31711635
贵州 -1.3196061 0.34762932
河南 -1.9794541 0.39454008
陕西 -0.8736815 0.50934383
安徽 -1.8264346 0.52788853
福建 0.2044823 1.35964846
江西 -2.2713675 1.89803737
海南 -1.1766527 1.94469519
广西 -0.2557057 2.09250406
广东 5.6758378 3.12277958
(2)碎石图

(3)散点图
> plot(score,xlim=c(-2.5,6.5),ylim=c(-3,3.5))
> text(score,rownames(data),pos=4,cex=0.6)#为散点图填标签
> abline(v=0,h=0,lty=3)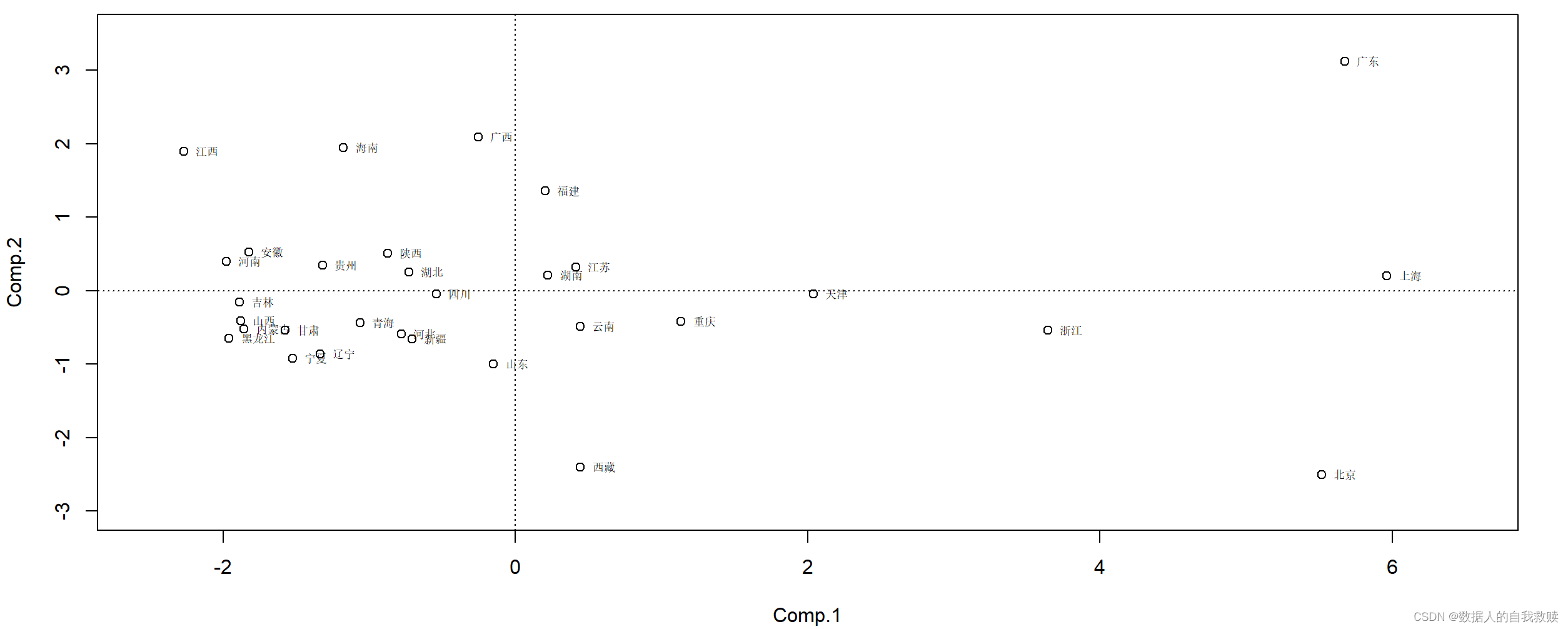
> biplot(princ)
Warning messages:
1: In doTryCatch(return(expr), name, parentenv, handler) :
display list redraw incomplete
2: In doTryCatch(return(expr), name, parentenv, handler) :
display list redraw incomplete 
二、因子分析
1.载荷矩阵求解
(1)主成分法
principal(r,nfactors=1,rotate="varimax",covar=FALSE,scores=TRUE,method="regression",cor="cor",...)"
r
a correlation matrix. If a raw data matrix is used, the correlations will be found using pairwise deletions for missing values.(相关矩阵)
nfactors
Number of components to extract(因子个数)
rotate
“none”, “varimax(最大方差法进行正交旋转)", "quartimax", "promax", "oblimin", "simplimax", and "cluster" are possible rotations/transformations of the solution.
covar
If false, find the correlation matrix from the raw data or convert to a correlation matrix if given a square matrix as input.(0-1变量)
scores
If TRUE, find component scores(0-1变量)
method
Which way of finding component scores should be used. The default is “regression”(默认用回归法计算因子得分)
(2)主因子法
fa(r,nfactors=1,scores="regression",SMC=TRUE,covar=FALSE,...)
【注】fa函数中有一个fm参数,若fm='pa'表示主因子法;fm=ml表示极大似然法
(3)极大似然法
factanal(x,factors,data=NULL,scores=c("none","regression","Bartlett"),totation="varimax",...)
此函数基于MLE法求载荷矩阵
x
数据矩阵或回归方程
factors
因子个数
data
如果X为回归方程,此处输入数据集
scores
计算因子得分的方法,包括’regression’和’Bartlett’
rotation
因子旋转方法
2.【例8.3.1】
(1)因子载荷图
> d8.3.1=read.csv('D:/个人成长/学业/课程/应用多元统计分析/上机/上机三/exec6.5.csv',header=1)
> data1=d8.3.1[,-(1:2)]
> rownames(data1)=d8.3.1[,1]
> install.packages("psych")
> library(psych)
> rc=principal(data1,nfactors=2,rotate="varimax",score=T)
> rc$loadings
Loadings:
RC1 RC2
x1 0.277 0.934
x2 0.379 0.892
x3 0.545 0.771
x4 0.714 0.625
x5 0.815 0.523
x6 0.903 0.386
x7 0.905 0.394
x8 0.936 0.258
RC1 RC2
SS loadings 4.202 3.298
Proportion Var 0.525 0.412
Cumulative Var 0.525 0.937
> factor.plot(rc)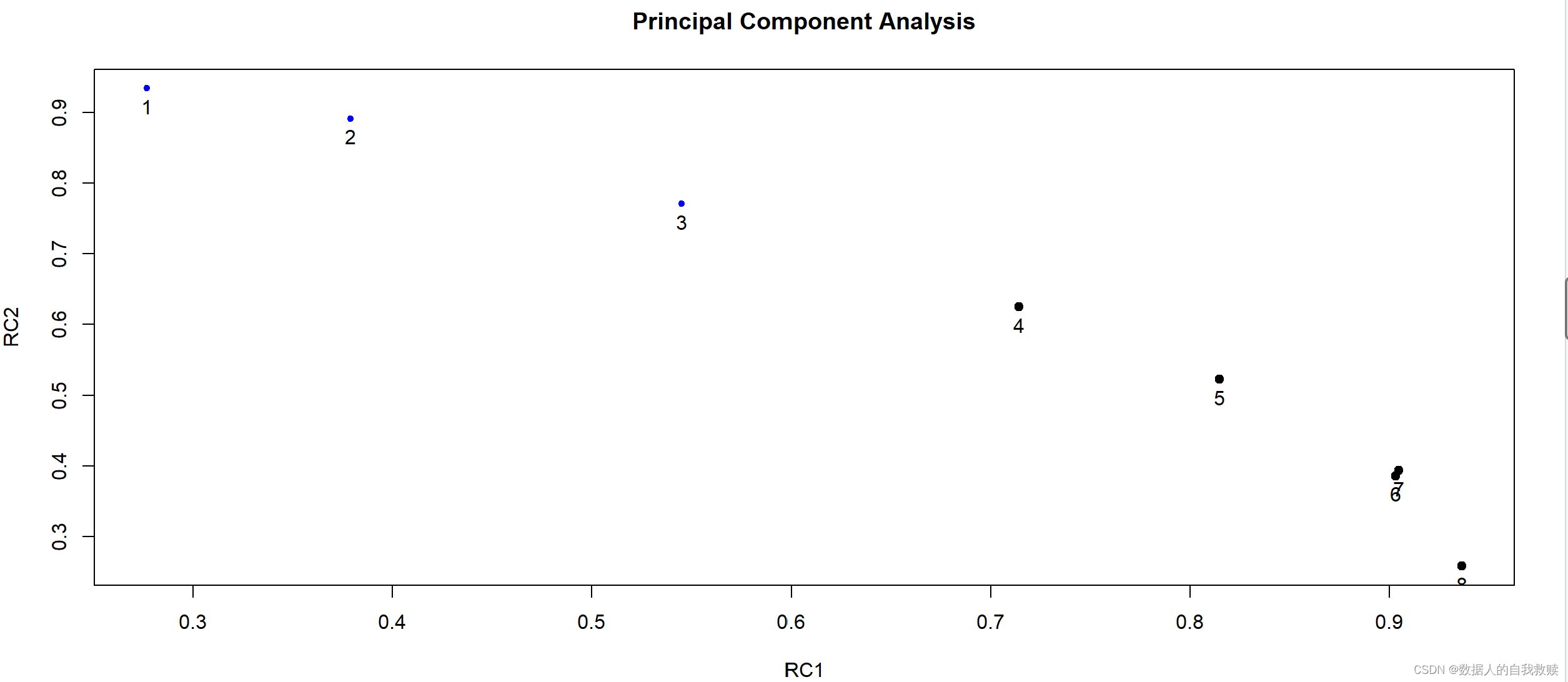
> rc
Principal Components Analysis
Call: principal(r = data1, nfactors = 2, rotate = "varimax", scores = T)
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 h2 u2 com
x1 0.28 0.93 0.95 0.050 1.2
x2 0.38 0.89 0.94 0.061 1.3
x3 0.55 0.77 0.89 0.108 1.8
x4 0.71 0.62 0.90 0.100 2.0
x5 0.81 0.52 0.94 0.062 1.7
x6 0.90 0.39 0.96 0.035 1.4
x7 0.90 0.39 0.97 0.027 1.4
x8 0.94 0.26 0.94 0.057 1.2
RC1 RC2
SS loadings 4.20 3.30
Proportion Var 0.53 0.41
Cumulative Var 0.53 0.94
Proportion Explained 0.56 0.44
Cumulative Proportion 0.56 1.00
Mean item complexity = 1.5
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is 0.02
with the empirical chi square 0.96 with prob < 1
Fit based upon off diagonal values = 1(2)因子得分散点图
>#作因子得分散点图
> score=rc$scores
> plot(score,xlim=c(-1.5,4),ylim=c(-2,2))
> text(score[,1],score[,2],d8.3.1[,1],pos=4,cex=0.6)
> abline(v=0,h=0,lty=3)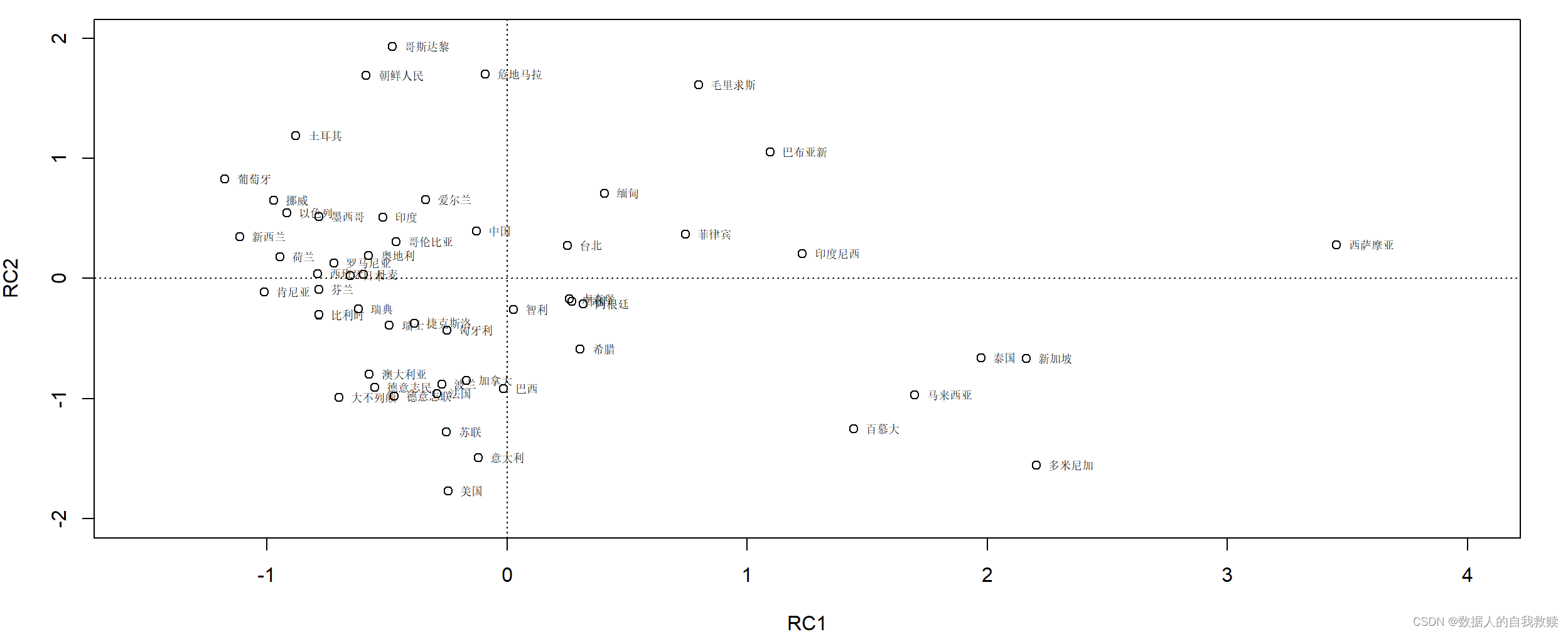
(3)其他结果
> fapa=fa(data1,nfactors=2,residuals=1,rotate='none',fm='pa',SMC=TRUE)
> fapa$communality#共性方差
x1 x2 x3 x4 x5 x6 x7
0.9200913 0.9149326 0.8558811 0.8784953 0.9249959 0.9621504 0.9786024
x8
0.9048802
> f1=factanal(data,factors=3,scores='regression',rotation='none') #不进行因子旋转
> f2=factanal(data,factors=3,scores='regression',rotation='varimax') #进行因子旋转
> f3=fa(data1,nfactors=2,residuals=1,rotate='varimax',fm='ml',scores='regression')#极大似然法
> cbind(f2$loadings,f3$loadings)#两种极似然函数的比较
Factor1 Factor2 Factor3 ML1 ML2
x1 0.81250225 0.4177888 0.18686638 0.2906638 0.9135222
x2 0.05733073 0.1811745 0.62006631 0.3819944 0.8821941
x3 0.39103668 0.7938804 0.15130940 0.5429947 0.7441257
x4 0.32298354 0.5755105 0.34903953 0.6912063 0.6220148
x5 0.83950427 0.3742963 -0.06225936 0.7985556 0.5297085
x6 0.48885989 0.8105823 0.14685468 0.9006595 0.3937239
x7 0.70505746 0.4688554 -0.52664365 0.9072054 0.3987749
x8 0.79291078 0.3728792 0.39667568 0.9147804 0.2778203
> cbind(f1$loadings,f2$loadings)#旋转与不旋转的比较
Factor1 Factor2 Factor3 Factor1 Factor2
x1 0.7310726 0.5469948 -0.1896204912 0.81250225 0.4177888
x2 -0.1387842 0.6326011 0.0338816889 0.05733073 0.1811745
x3 0.6262363 0.5288842 0.3662786146 0.39103668 0.7938804
x4 0.3777003 0.6076627 0.2131850102 0.32298354 0.5755105
x5 0.8387414 0.3175494 -0.2107524126 0.83950427 0.3742963
x6 0.7090511 0.5587981 0.3202891336 0.48885989 0.8105823
x7 0.9920715 -0.1003940 0.0001581675 0.70505746 0.4688554
x8 0.6012630 0.7121045 -0.2376718245 0.79291078 0.3728792
Factor3
x1 0.18686638
x2 0.62006631
x3 0.15130940
x4 0.34903953
x5 -0.06225936
x6 0.14685468
x7 -0.52664365
x8 0.39667568
> f3=fa(data1,nfactors=2,residuals=1,rotate='varimax',fm='ml',scores='regression')#极大似然法
> f4=fa(data1,nfactors=3,residuals=1,rotate='varimax',fm='ml',scores='regression')#极大似然法
> cbind(f3$loadings,f4$loadings)#极大似然估计时因子数为2、3时载荷的变化
ML1 ML2 ML2 ML1 ML3
x1 0.2906638 0.9135222 0.2842157 0.9558980 -0.02202328
x2 0.3819944 0.8821941 0.3945883 0.8505448 0.11893540
x3 0.5429947 0.7441257 0.5425322 0.7231244 0.19593117
x4 0.6912063 0.6220148 0.6819987 0.5952693 0.31649347
x5 0.7985556 0.5297085 0.7960893 0.5015629 0.24148913
x6 0.9006595 0.3937239 0.8999463 0.3823990 0.07783062
x7 0.9072054 0.3987749 0.9134103 0.3910853 0.04336762
x8 0.9147804 0.2778203 0.9136076 0.2732810 0.04140327
>f5=fa(data1,nfactors=2,residuals=1,rotate='varimax',fm='pa',SMC=TRUE,scores='regression')
>f6=fa(data1,nfactors=3,residuals=1,rotate='varimax',fm='pa',SMC=TRUE,scores='regression')
>cbind(f5$loadings,f6$loadings)#因子法因子数为2、3时载荷的变化
PA1 PA2 PA1 PA2 PA3
x1 0.2874749 0.9151226 0.2853996 0.9408787 0.01829471
x2 0.3862979 0.8750466 0.3916530 0.8594109 0.10132871
x3 0.5494251 0.7443206 0.5378983 0.7239969 0.20653223
x4 0.7023221 0.6206762 0.6758104 0.5896396 0.37448481
x5 0.8036262 0.5283757 0.7883568 0.5063299 0.23180188
x6 0.8999406 0.3902016 0.9011275 0.3852969 0.07944727
x7 0.9068638 0.3952220 0.9125000 0.3915608 0.06011715
x8 0.9098101 0.2777153 0.9093455 0.2740464 0.07273407
> score2 = f2$scores
> score2[order(score2[,'Factor1'],decreasing = 1),]#按因子得分排序
Factor1 Factor2 Factor3
广东 3.33674409 0.52139366 -2.395531713
上海 1.83017434 1.79755430 0.774666596
西藏 1.79342081 -2.31242388 2.163976416
福建 1.05121757 -0.97092898 -0.651398494
浙江 0.68294892 1.20379707 0.330447936
云南 0.67410328 -0.49590178 0.734547991
北京 0.61690935 2.35712742 2.362492964
海南 0.49619798 -1.30793110 0.766609051
广西 0.24126238 0.12974880 -1.323097526
天津 0.20149003 1.23907591 -0.179894171
江苏 -0.06819937 0.31503513 0.183193390
江西 -0.16489626 -0.67961943 -1.685661168
四川 -0.20606433 0.05539039 -0.211819118
湖南 -0.23067601 0.65149506 -0.428785236
重庆 -0.24295199 0.84082415 0.295104355
青海 -0.34079562 -0.52906025 0.663241417
河南 -0.37274952 -0.70837638 -0.995527657
湖北 -0.39028240 0.41263966 -1.169584699
陕西 -0.57729498 0.27883783 -0.933415065
山西 -0.57835215 -0.62724603 0.346606148
贵州 -0.58120801 -0.21398455 -0.033523114
甘肃 -0.60018143 -0.50747397 0.773326069
辽宁 -0.61746685 -0.38257578 -0.034667985
新疆 -0.67288853 0.20963537 0.249966648
内蒙古 -0.70682222 -0.45844783 0.245571801
黑龙江 -0.72074801 -0.62817973 -0.242568683
吉林 -0.72649221 -0.34831537 -0.487998697
河北 -0.75987901 0.23450927 -0.070620735
安徽 -0.77010307 -0.26911947 0.003528822
宁夏 -0.79230623 -0.51462318 0.735839060
山东 -0.80411056 0.70714371 0.214975398