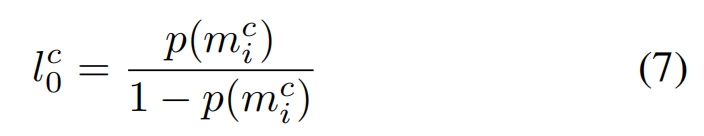0. 简介

作为Transformer在机器视觉领域的爆火，在自动驾驶领域目前很多工作都集中在前视转鸟瞰图的方法中，这里我们来讲2020年一篇经典的论文《Predicting Semantic Map Representations from Images using Pyramid Occupancy Networks》，其工作被近两年的新的BEV算法进行充分的验证以及对比，从今天的眼光来看，这项工作的思想仍然是非常好的。论文通过使用Transformer算法，通过单目视觉检测俯视图下(BEV (bird eye view))车辆建立语义地图，并通过贝叶斯概率建立多帧之间的地图关系。这是这篇文章的Github开源网址

1. 文章贡献

这篇文章作为一篇前视转BEV文章。其输入和输出分别是环视单目摄像头以及周围360°的BEV语义分割地图。
在这里插入图片描述
本文作者指出，该文章主要有三个主要创新点：

提出了一种新型的密集Transformer变换层，从而将基于图像的特征映射映射到鸟瞰空间。（这部分工作应该是最关键的工作）
设计了一个深度卷积神经网络体系结构，其中包括在多个图像尺度下运行的变压器金字塔，从单目图像预测精确的鸟瞰图。（这部分工作与前面该作者工作类似）
在两个大规模自动驾驶数据集上评估了作者的方法

但是实际上文中还有一点比较值得借鉴的就是贝叶斯概率建立多帧之间的地图关系。这虽然不是作者提出的方法，但是影响到了后面的前视转BEV领域。下面该文的要点。

视图变换：使用了密集transformation层。单纯的就是个homography 变换，只是在不同分辨率上硬性切段来实现拼接。
概率语义占用网格表示的方法便于摄像机和帧之间的融合。本质上，我们需要预测BEV网格的多类二进制标签
loss ：加权二进制CE+不确定性损失，使得不可见的feature map上概率接近0.5.
Bayesian occupancy grid 操作。 log-odds使用，把概率p转化到log-odds，然后进行时间维度合并，最后通过个sigmoid操作转化回概率，从而用于多摄像机和时间融合。
结构方面：
密集变换Transform内部主要有三点：（1）1D conv将高度尺寸折叠为固定特征向量（2）1D conv扩展沿深度轴扩展特征向量（3）使用内部函数重新采样到笛卡尔框架
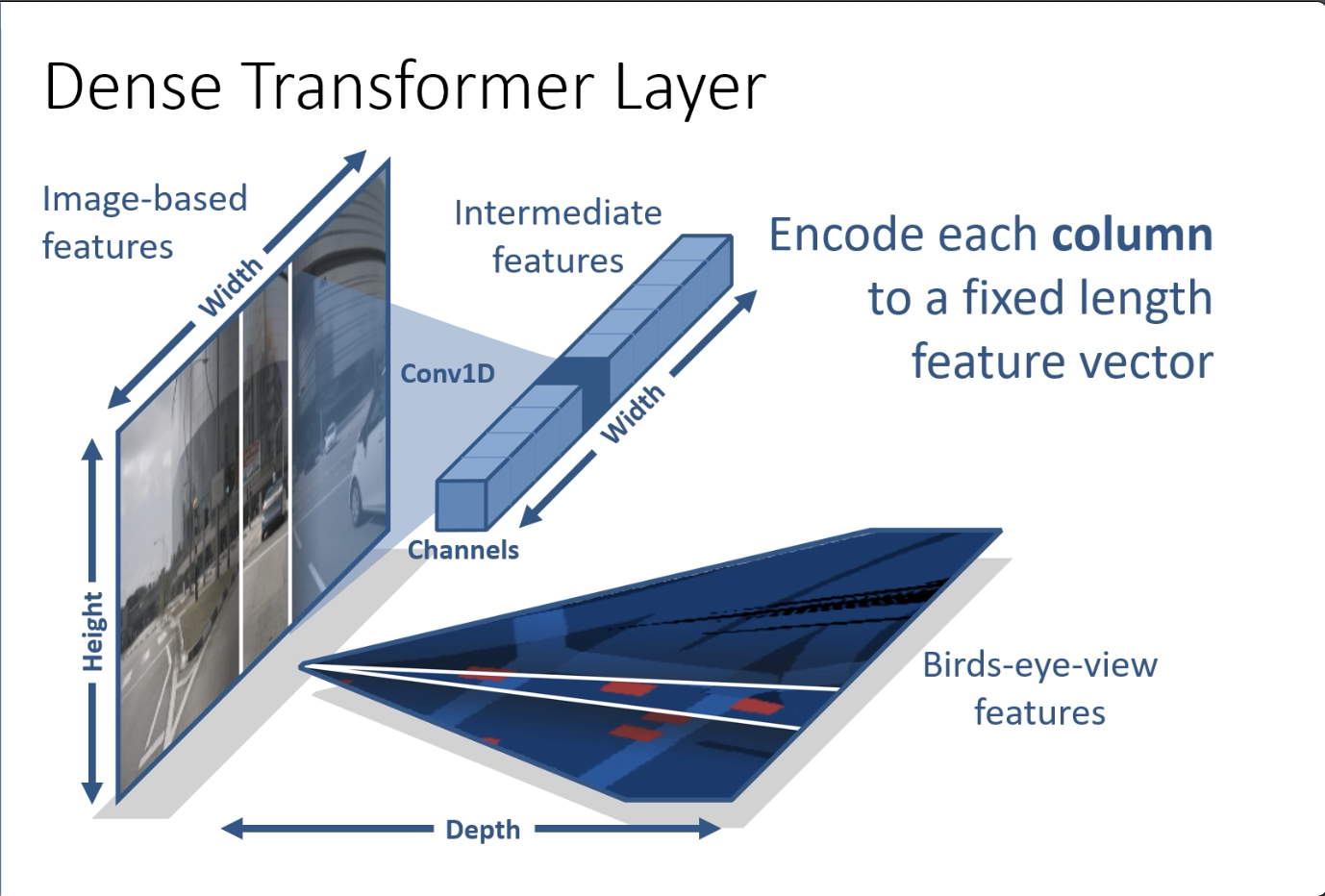
```
 多尺度变换金字塔：每一层负责变换BEV中图像的一部分
```

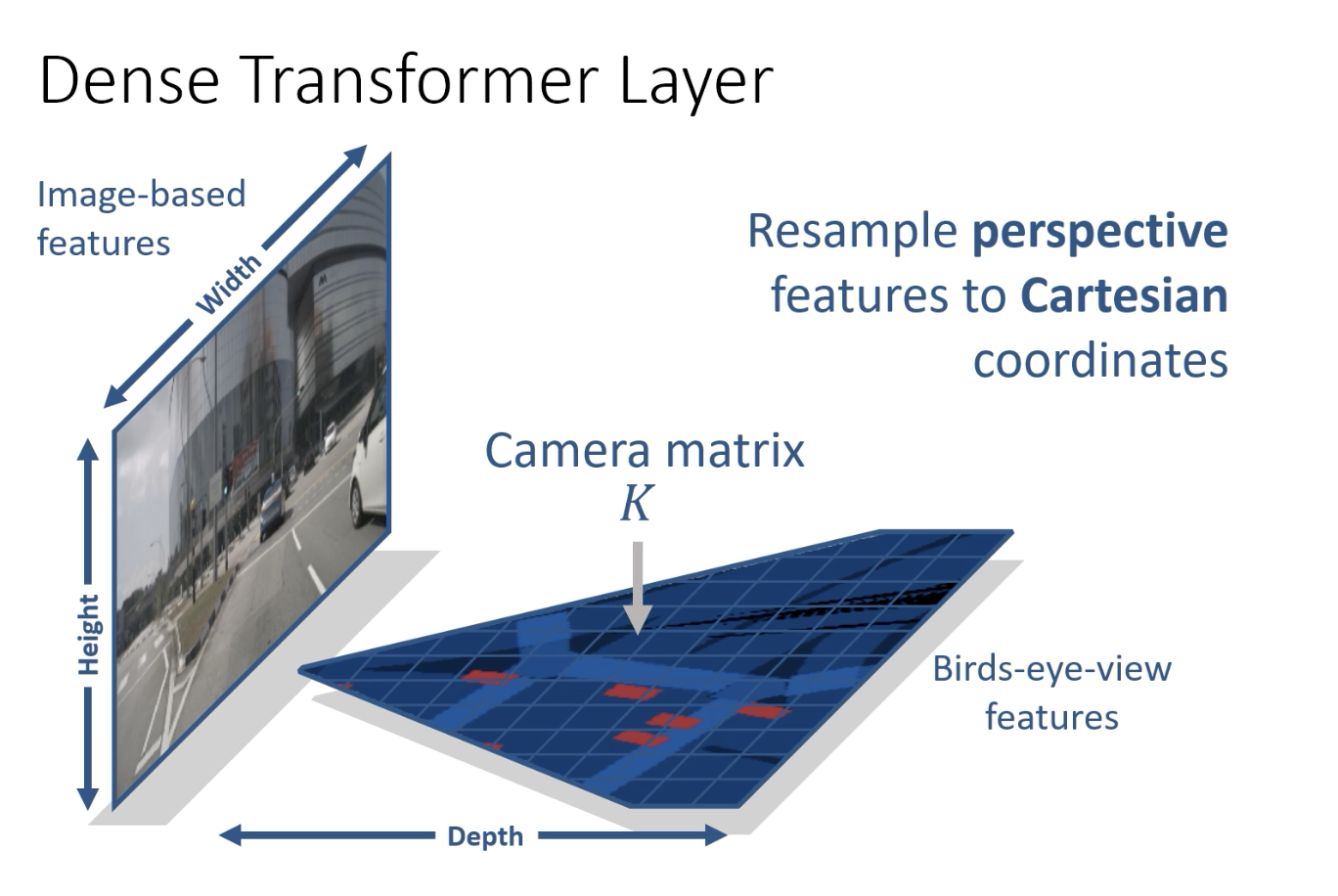
在这里插入图片描述

2. 具体算法

该作者为《Orthographic Feature Transform for Monocular 3D Object Detection》一文的作者，其大致的结构做了保留下图的结构
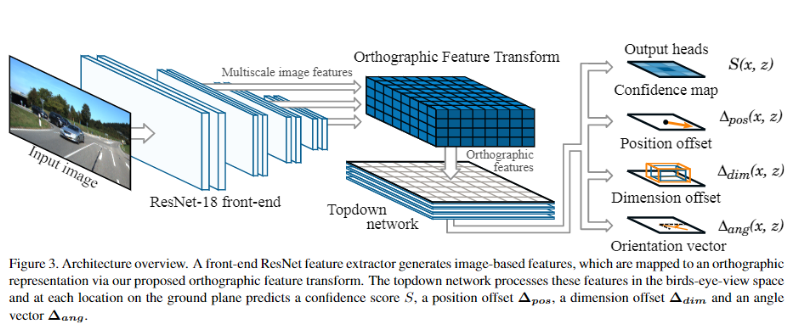
在这里插入图片描述
该文的结构如下图所示，我们可以发现其与OFT的feature transformation上有很大的进步，主要存在有两点：

使用FPN网络得到multi-scale的特征，对每一个特征都转成BEV
不同scale的特征对应不同的BEV上的距离(这点很intuitive，在OFT实际训练的时候会发现受制于分辨率，OFT沿着一条射线上的格点几乎就是很长的区域都是同一个值，使用不同特征对应不同的距离，一方面可以打破这个不良的特性，增强BEV上的信息裕度，另一方面也很符合不同scale上感受野与物体大小的特性，当然又被《Translating Images into Maps》通过给进一步提升了)。同时由于转到了BEV上，作者自然地进一步想到了对时序信息上进行融合，这样预测出来的BEV上的occupancy map就可以用贝叶斯方法直接更新。

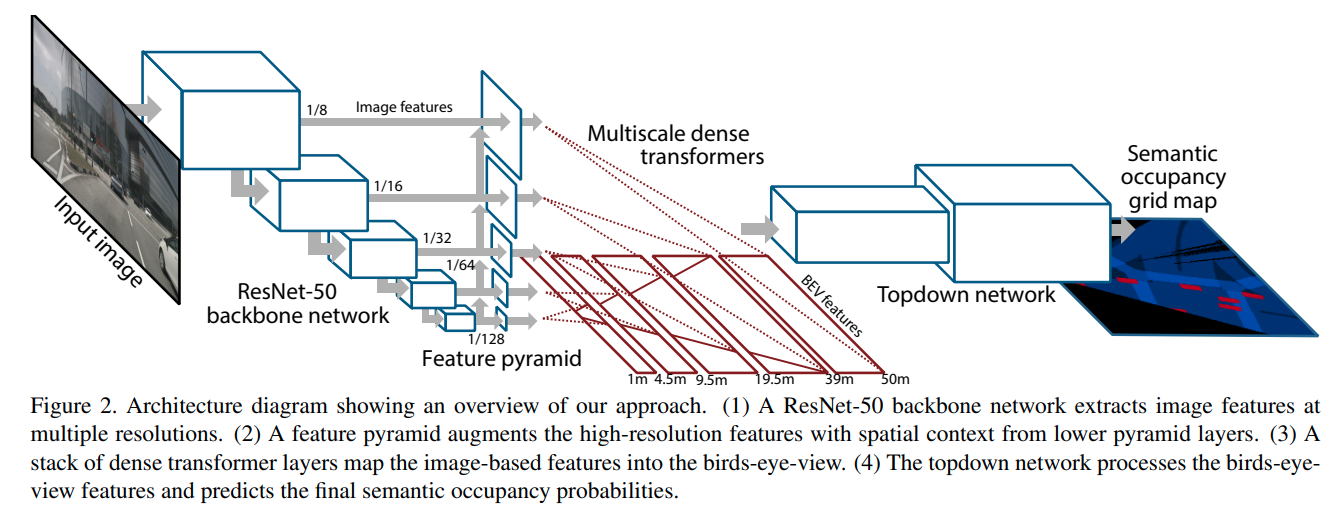
整个网络有四部分：
（1）ResNet-50骨干网络以多种分辨率提取图像特征。
（2）特征金字塔通过较低金字塔层的空间上下文来增强高分辨率特征。
（3）一组密集变换层（dense transformer layers）将基于图像的特征映射到鸟瞰图。
（4）自上而下网络（top down network）处理鸟瞰特征并预测最终的语义占用（semantic occupancy）概率。

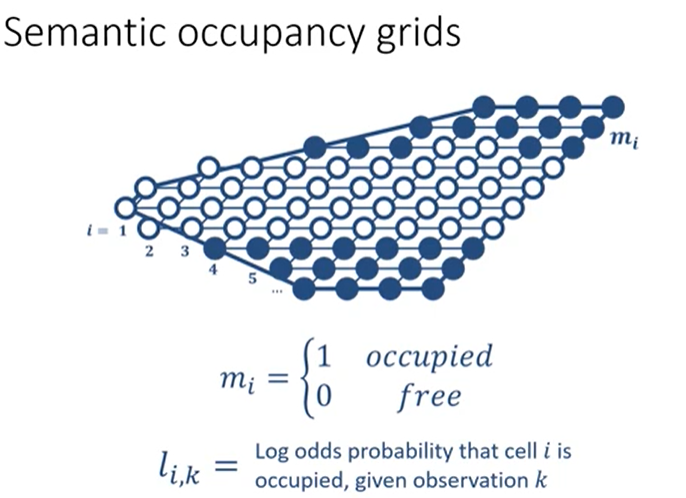
2.1 占用栅格地图

传统的占用网格映射中，占用概率 $p(m_i |z_t)$ 使用反向传感器模型进行估计，该模型通常是一个简单的手工设计函数，根据传感器特性从距离传感器读数映射到占用概率。但是文中的观察是依据图像的，它需要学习从单眼输入图像预测占用概率。为此文中基于Occupancy grid结构，通过CNN去模拟每个网格某种分类obj出现的 $p(m^c_i |z_t)$ 后验估概率密度函数 $f_θ(z_t, x_i)$ 。

作者的目标是在二维鸟瞰图像的每个位置上预测一组多类二值标签。这个场景与被广泛研究的计算机视觉语义分割问题有许多相似之处。然而，让这项任务特别具有挑战性的是，输入和输出表示存在于完全不同的坐标系中:前者存在于透视图像空间，后者存在于正投影鸟瞰空间。因此，我们提出了一个简单的Transformer层，使其既利用了摄像机的几何形状，又利用了全连接。
在这里插入图片描述

2.2 Loss损失函数

总体设计还是一个多分类的交叉熵，但是为了处理小物体不均衡的问题加入了αc作为权重因子
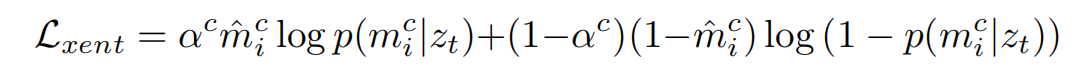
在这里插入图片描述
对于不确定性高的区域，比如遮挡，额外加上这个衡量不确定性的交叉熵

整个目标函数如上，λ = 0.001

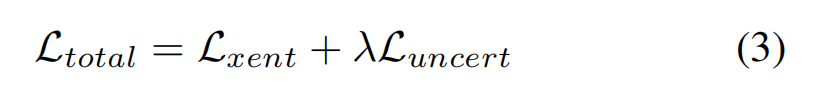
2.3 时间和传感器数据融合

这部分主要讲了使用贝叶斯占用栅格的思路，贝叶斯占用网格公式提供了一种使用贝叶斯滤波方法将多个观察结果和多个时间步上的信息结合起来的自然方法。考虑一个由具有外部矩阵Mt的相机拍摄的图像观测 $z_t$ 。我们首先将占用概率 $p(m^c_i|z_t)$ 变为对数-赔率表示,将后验估加了log，变成了类似sigmoid的形式
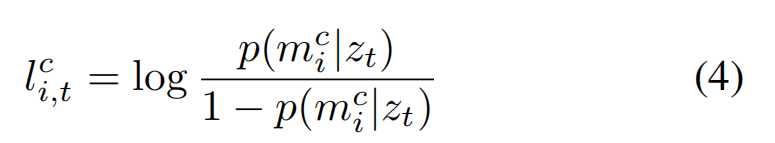
在这里插入图片描述
接下来还是一个全概率公式，因为加了log形式，其实还是概率相乘

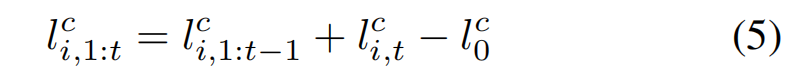
这里是对公式（4）的倒推，目的是通过sigmoid函数，即 $l^c_{i,1:t}$ ，来计算其后验概率

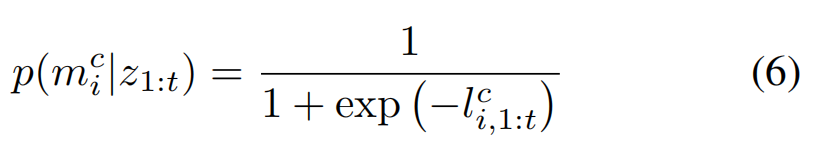
然后计算先验分布