从信号处理角度来说

分析平稳信号所蕴涵的信息, 一般地Fourier 变换就能应付自如。但以不稳定动力系统为特征的物理世界, 信号往往具有如下特点: 非平稳、非线性、非确定、非可积、非连续、非光滑、非周期、非对称等等。使用Fourier 变换分析、解释非平稳信号, 就显得无能为力了。科学的本质在于解释世界, 对于同一客体, 不同的理论会有不同的解释。正是理论决定了我们所能观察的内容，以方波信号为例, Fourier变换“看到”的方波, 是由无穷多个正弦波组成的(不论Gibbs 现象), 然而Walsh变换“看到”的方波，就仅为一个方波。这两种变换对同一客体(方波)的解释之所以有如此大的差别, 是因为它们所采用的基函数相异: Fourier变换的基函数是无始无终的等幅谐波, 而Walsh 变换的基函数则为方波。

信号应与物质一样, 具有不同的层次结构，物质的层次结构愈小, 其间的结合能则愈大, 将其分离就愈困难(需要更强大的粒子加速器)。而信号的层次结构却与之相反—层次结构愈小愈简单, 其间的结合能也愈小, 用Fourier变换就能容易地将待分析信号分解成正弦波的加权和; 信号的层次结构愈大愈复杂, 其间的结合能亦愈大, 要分离这些层次结构, 就需要更复杂的变换和更大量的计算。因此需要有各种变换, 以应对不同的信号层次结构。而从信号处理实际出发, 不同的现实信号需要不同的信号表示方法来相应处理。

 

 

 

 

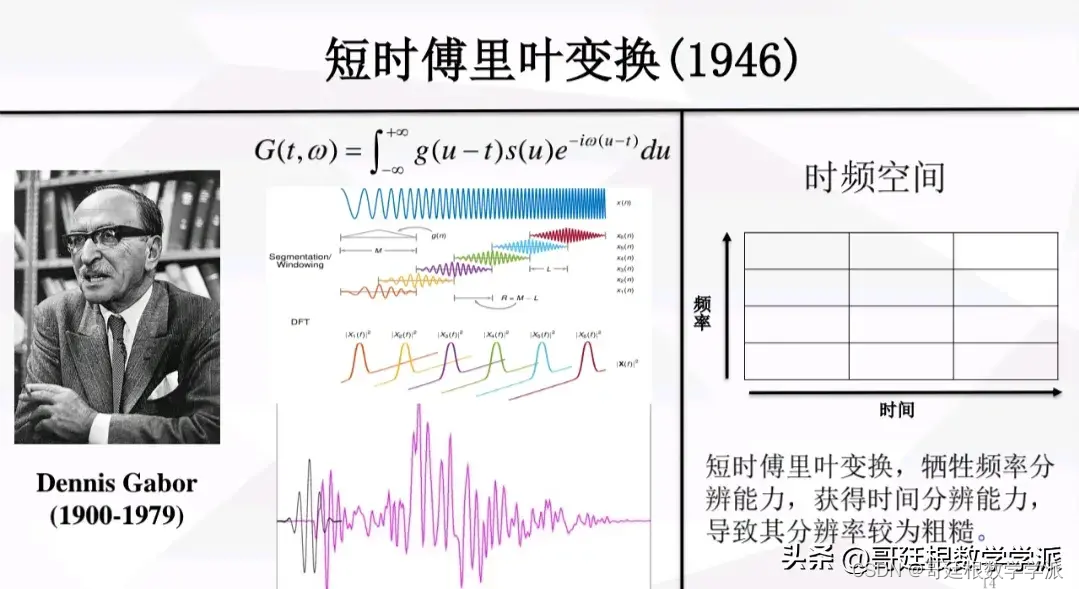
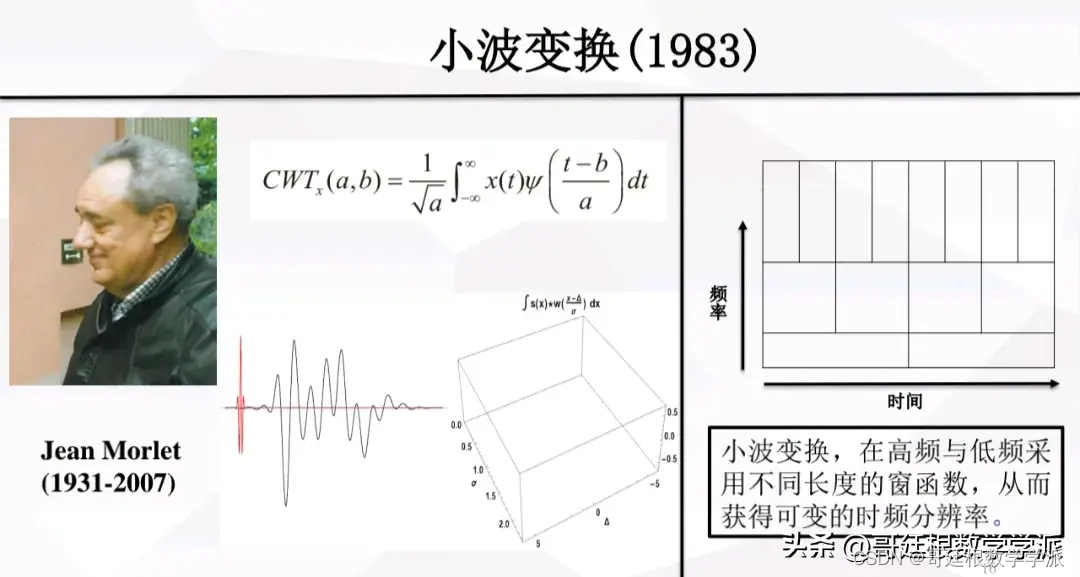
相关的文章参考

几种信号降噪算法（第一部分）

https://www.toutiao.com/article/7190201924820402721/

几种信号降噪算法（第二部分）

https://www.toutiao.com/article/7190270349236683264/

机械故障诊断及工业工程故障诊断若干例子（第一篇）

https://www.toutiao.com/article/7193957227231855163/

知乎咨询:哥廷根数学学派

算法代码地址：mbd.pub/o/GeBENHAGEN

擅长现代信号处理(改进小波分析系列，改进变分模态分解，改进经验小波变换，改进辛几何模态分解等等)，改进机器学习，改进深度学习，机械故障诊断，改进时间序列分析(金融信号，心电信号，振动信号等)