张量、标量、向量和矩阵

https://github.com/bovem/publications/tree/master/Linear%20Algebra

张量是一个数据数组(数字、函数等)，它以任意数量(0 或更大)的维度展开。维数称为张量秩。

秩 0 张量 没有维度(0)的张量。

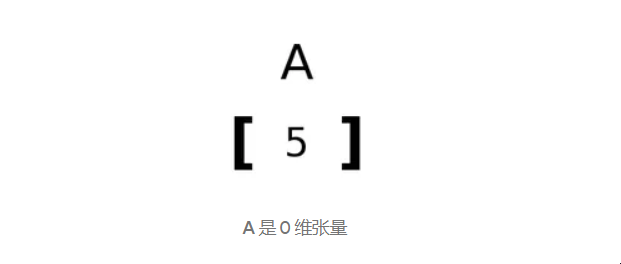
A 是 0 维张量 秩 1 张量 仅在一维中展开的张量。

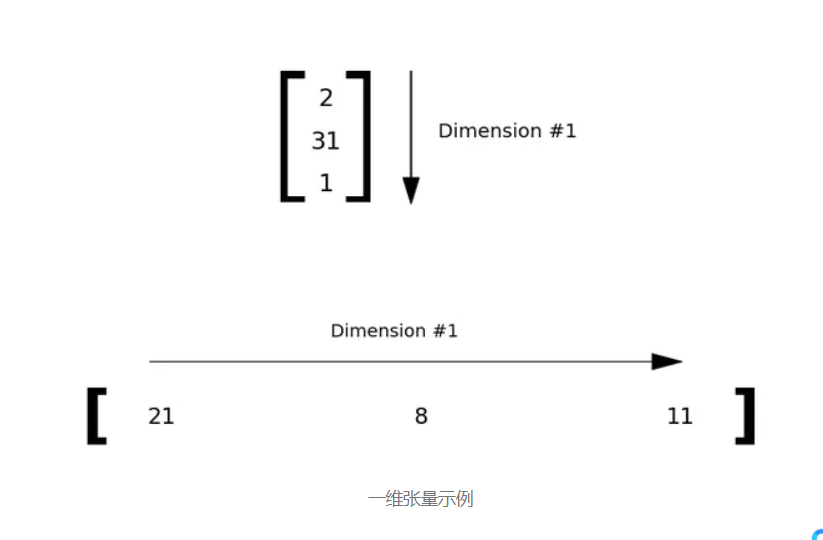
一维张量示例 秩 2 张量

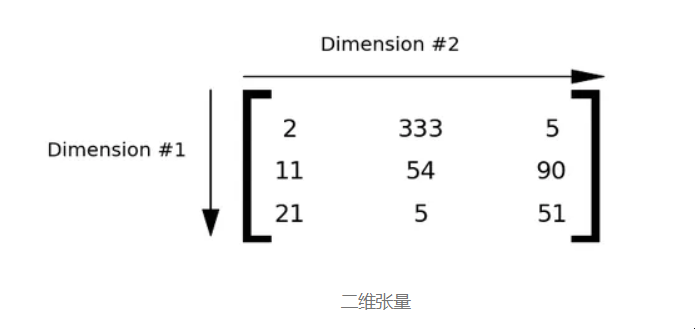
二维张量 秩 3 张量

三维张量就像矩阵一个接一个地放置

如图所示，秩 3 张量具有立方体(或长方体状结构)。

如果张量的秩超过 3，则很难可视化。

视频给出的解释直观深刻

Dan Fleisch给出了张量的惊人解释

标量

标量是 0 秩张量。在物理学中，各种量表示为标量，例如：距离（500公里），温度（10ºC），速度（34公里/小时）等。

向量

秩 1 张量称为向量。物理量，如速度(10 m/s)、位移(向东 54 m)、电磁场 (1 V/m)。

标量和矢量的区别：

不需要其他信息(如方向)的量(如温度)表示为标量。然而，需要指定方向的量与其大小一起用向量(如电场)表示。

E 是向量或秩 1 张量

向量用粗体字母,如“E”或字母上方的箭头表示。

为了绘制一个向量，我们使用它的元素作为坐标的值(分别为x，y和z轴)。在这里，第一个元素(0.5)被当作x值，第二个元素(0.5)被当作y值,如果我们有三个元素，第三个就是z值。

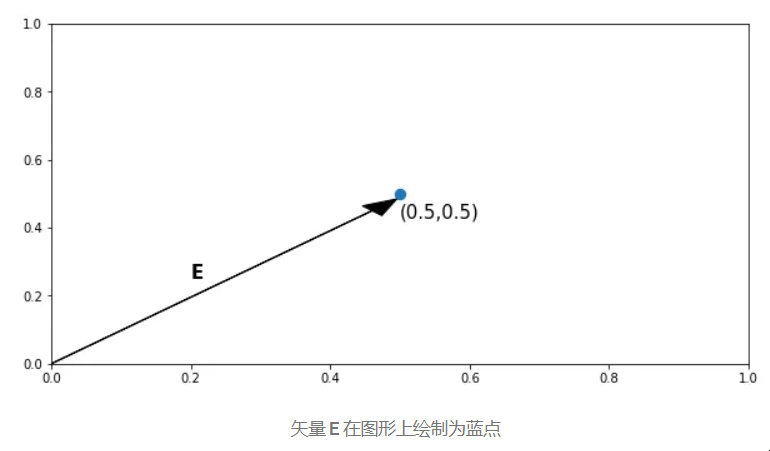
矢量 E 在图形上绘制为蓝点

将向量绘制为点后，我们从原点 （0，0） 向它放置一个箭头。

向量只是具有一行（称为列向量）或一列（称为行向量）的矩阵。

矩阵

矩阵是秩 2 张量。我们之前已经看过矩阵。

秩大于 2 的张量简称为“张量”(秩大于 2 的张量没有特定名称)。

张量的概念将矩阵、向量和标量推广到一个屋檐下(它们都是张量，但秩不同)。

矩阵作为向量的乘积：

当两个向量相乘时，它们形成一个矩阵。

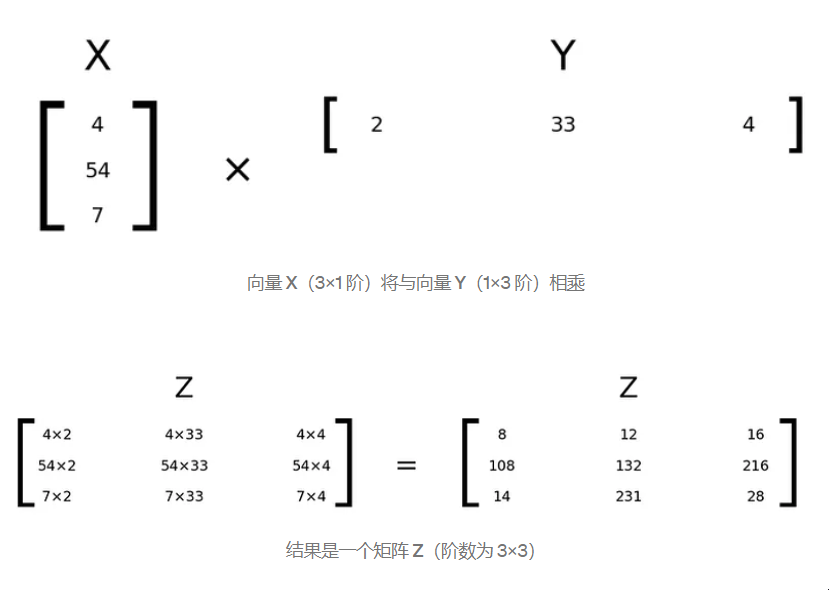
向量 X(3×1 阶)将与向量 Y(1×3 阶)相乘

结果是一个矩阵 Z(阶数为 3×3)

向量 X 和 Y 组合起来有 6 个元素，但它们的乘积本身就有 9 个元素。因此，一些矩阵可以分解为两个向量的乘积。

假设线性方程组如下：

3x-5y = 6 →（1）

x+y = 4 →（2）

3x+y = 0 →（3）

该系统在行图中的表示为：

行图片可以绘制在图上：

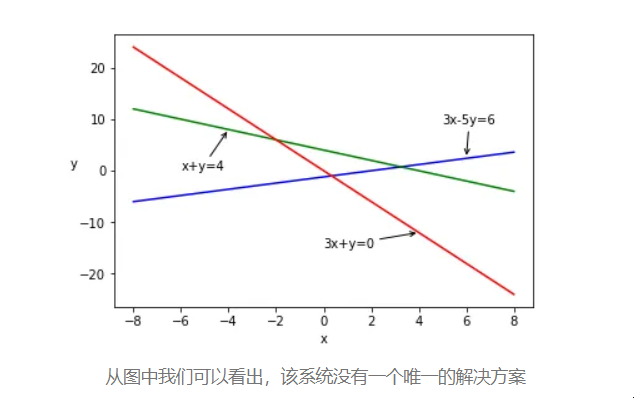
从图中我们可以看出，该系统没有一个唯一的解决方案.

为了从行图片中找到线性方程组的解，我们查看图形，看看所有线是否有任何一个交点，该点称为方程组解。

如果没有共同点，那么方程组就没有解（如上例所示）。

列图片

列图是为每个变量单独形成的系数矩阵。之后，变量与其系数矩阵（标量乘法）相乘并相加。

然后，它等同于常数矩阵。

取线性方程组(1)、(2)和(3)，列图如下：

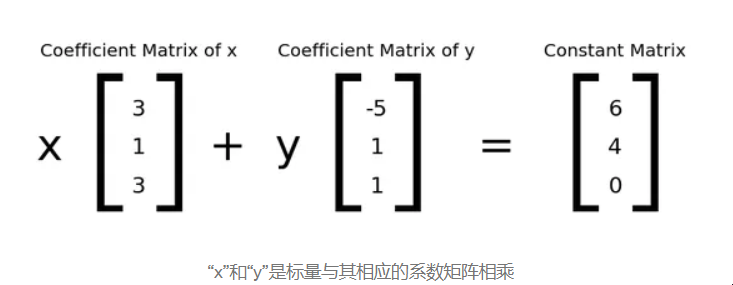
“x”和“y”是标量与其相应的系数矩阵相乘

图表上的列图片

为了在图上显示列图片，我们将单个系数矩阵视为向量，并将这些向量绘制在图上。

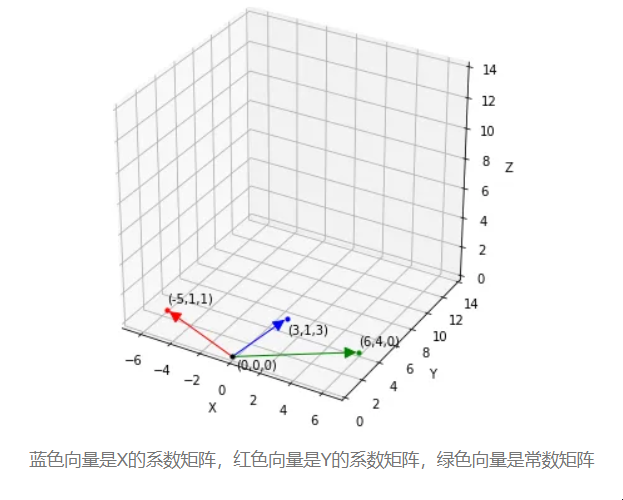
蓝色向量是X的系数矩阵，红色向量是Y的系数矩阵，绿色向量是常数矩阵

为了从列图片中找到方程组的解，我们将系数矩阵与不同的变量值(x 和 y)相乘并将它们相加(向量加法类似于矩阵加法)。

如果结果等于常数矩阵，则x和y的值称为线性方程组解。

对于此示例，正如我们在行图片中看到的那样，没有解决方案。因此，对于列图片中没有 x 和 y 的值，总和向量将等于常量矩阵(或向量)。

在寻找任何线性方程组的解时，我们可能会遇到以下三种情况之一 一个独特的解决方案 考虑一个线性方程组：

4x+y = 9→(4)

2x-y = 3→（5）

5x-3y = 7→(6)

将这些方程绘制为图表上的行图片和列图片：

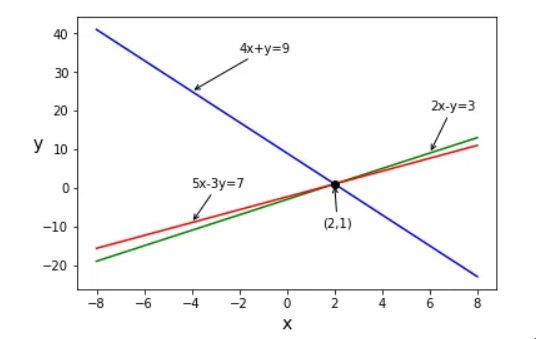
(4)(5)和(6)的行图片

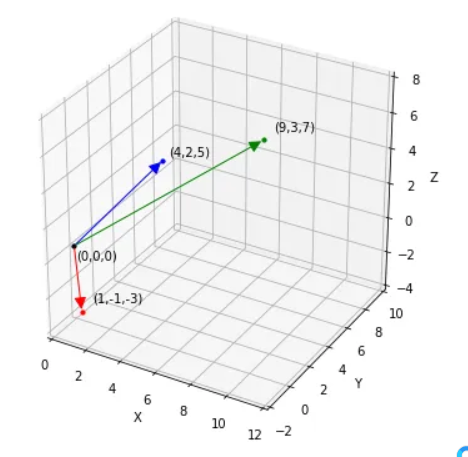
(4)(5)和(6)的列图片

为了验证解决方案 x= 2 和 y=1，我们从列图片中替换它们的值并计算。

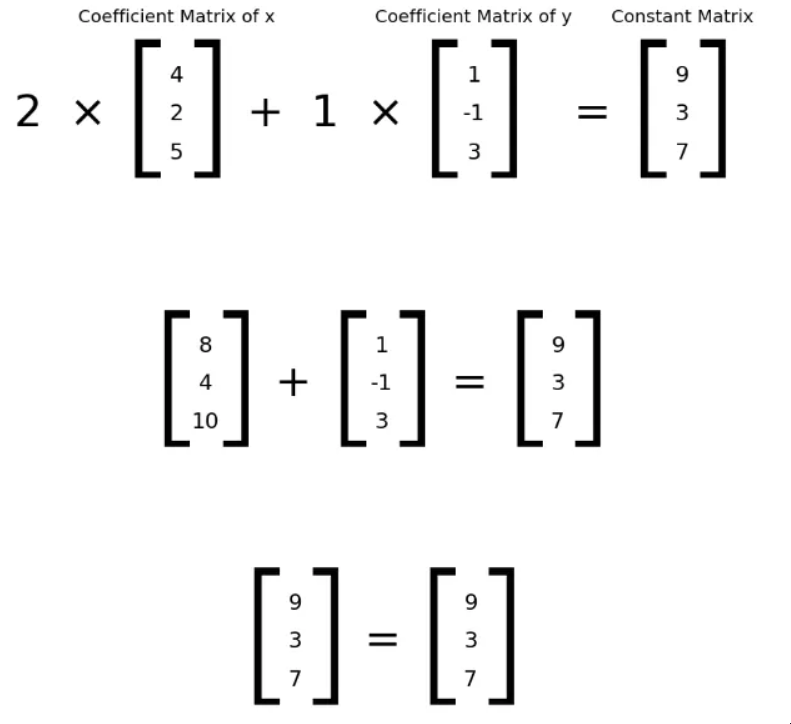
因此，结果等于常量矩阵。因此，x=2 和 y=1 是方程组(4)(5)和(6)的一个唯一解。

无限多的解决方案 考虑一个线性方程组：

x+2y = 4→(7)

2x+4y = 8→(8)

将这些方程绘制为图表上的行图片和列图片：

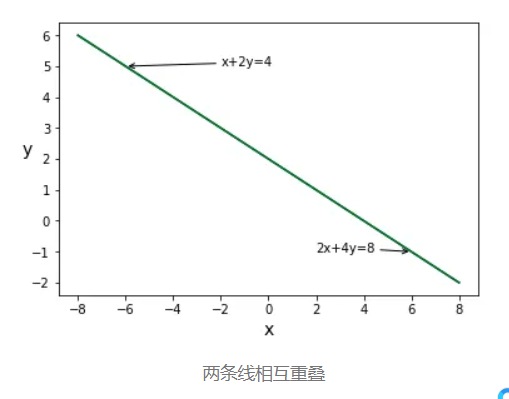
两条线相互重叠

在这里，我们有解决方案，但它们的数量无限大,因为两条线几乎在每个点上相交。

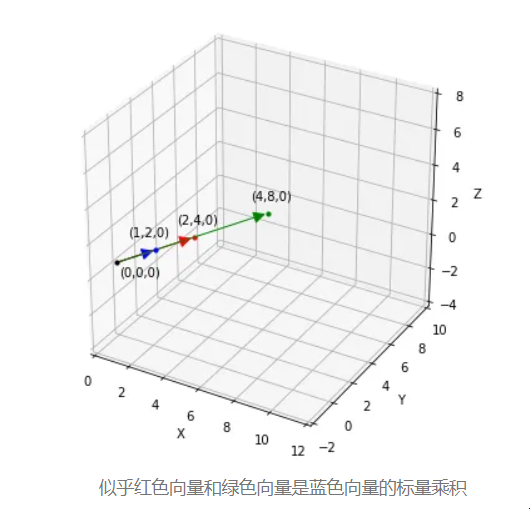
似乎红色向量和绿色向量是蓝色向量的标量乘积

因此，x 和 y 可能有无限多的值，以便列图片返回常量矩阵。

没有解决方案

考虑一个线性方程组：

x+y = 4→(9)

x+y = 8→(10)

x-y = 0→(11)

将这些方程绘制为图表上的行图片和列图片：

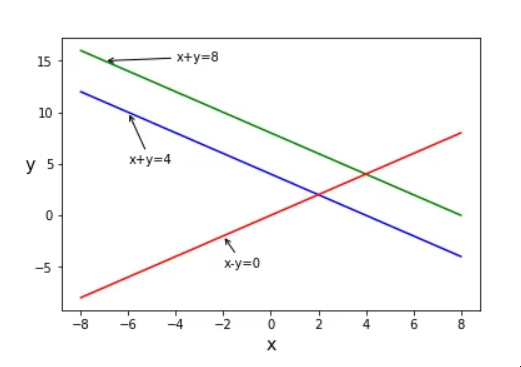
所有三条线都没有交点

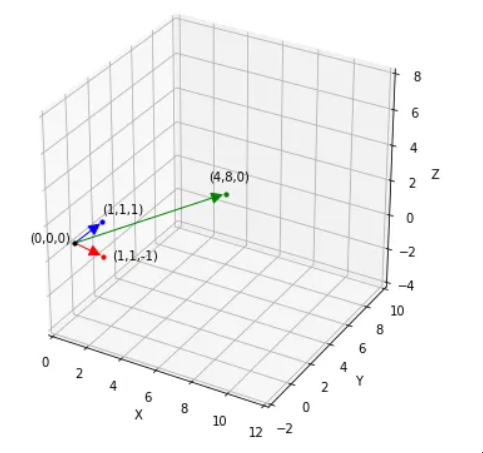
我们可以看到“x”和“y”的无解

通过行和列图片乘法

除了前面讨论的矩阵乘法方式之外，我们还可以通过另外两种方式进行乘法

上：行图片乘法

中：当一个矩阵的各个列与另一个矩阵的行（标量乘法）相乘时，结果矩阵相加。

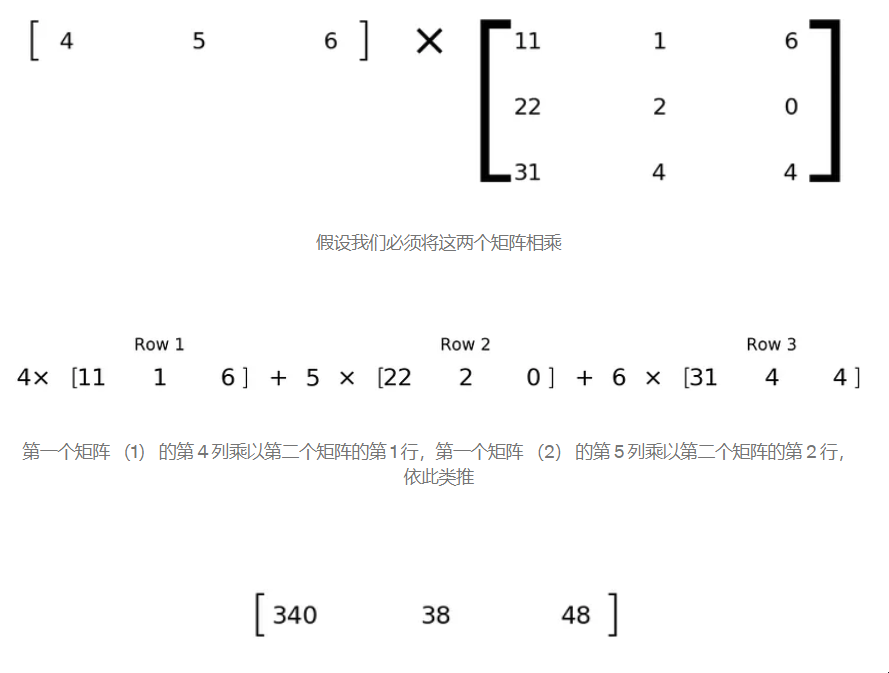
下：假设我们必须将这两个矩阵相乘

第一个矩阵(1)的第 4 列乘以第二个矩阵的第 1 行，第一个矩阵(2)的第 5 列乘以第二个矩阵的第 2 行，依此类推

结果正是我们对正常乘法的预期!

其他资源 ：

物理和工程学生张量简介 Joseph C. Kolecki,将在课堂精讲中分享