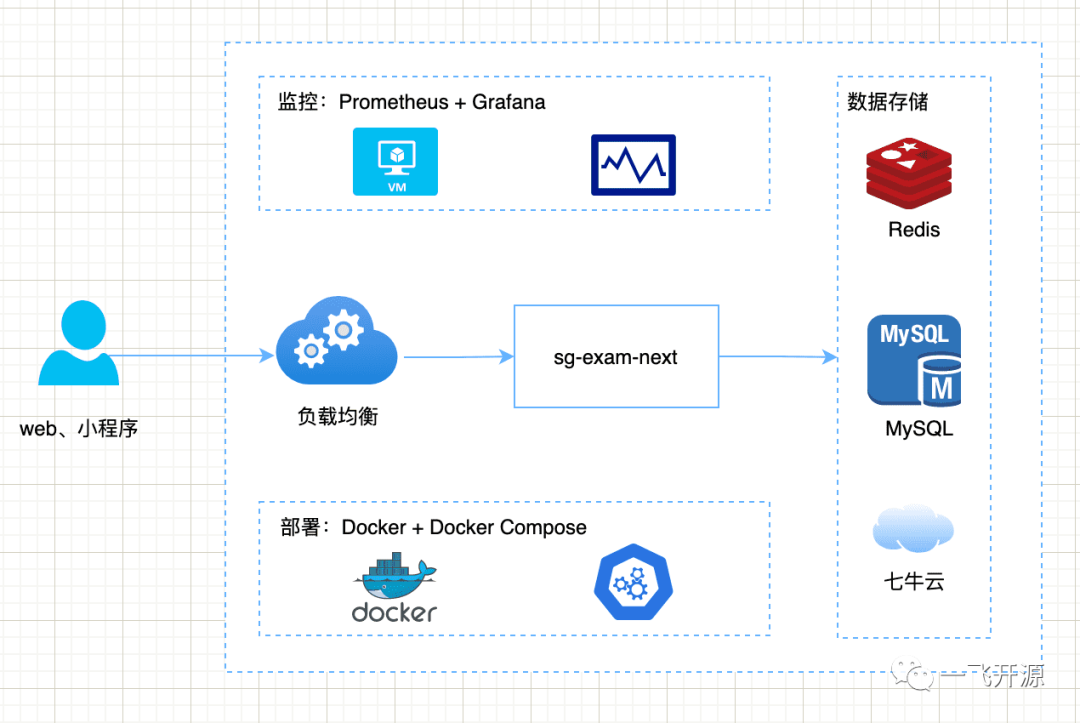
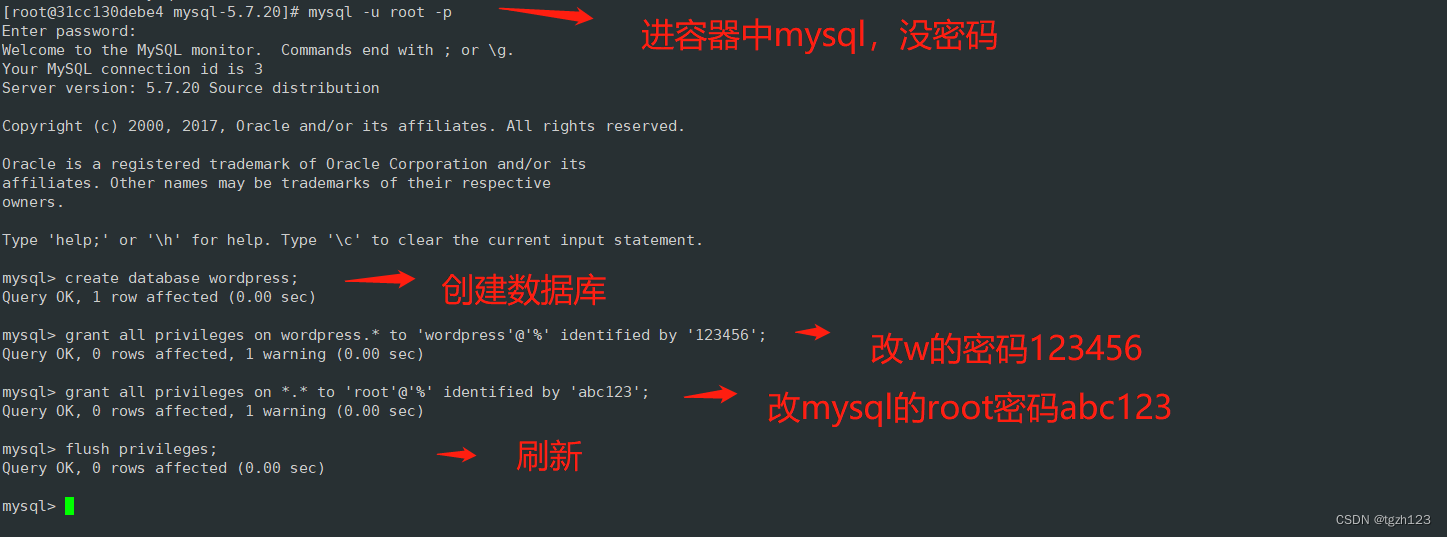
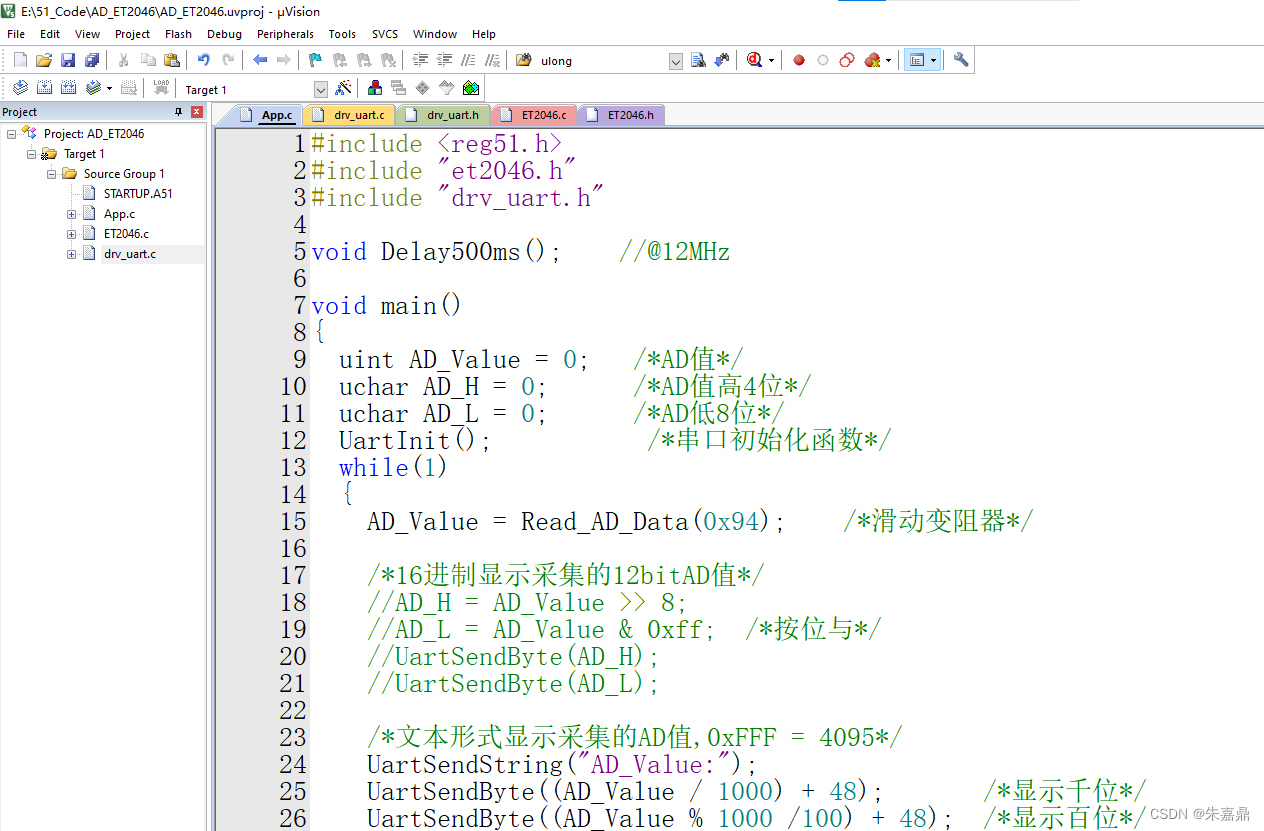
XGBoost有两种实现，原生版本和Sklearn版本，我选的是sklearn的主要是都用sklearn方便

参数

参数表
在这里插入图片描述

class xgboost.XGBRegressor ( max_depth=3, learning_rate=0.1, n_estimators=100, silent=True, objective='reg:linear', booster='gbtree', n_jobs=1, nthread=None, gamma=0, min_child_weight=1, max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1, scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None, importance_type='gain', **kwargs)

n_estimators:

在这里插入图片描述

n_estimators越大，模型的学习能力就会越强，模型也越容易过拟合。这个参数非常强大，常常能够一次性将模型调整到极限

subsample

在这里插入图片描述

确认了有多少棵树之后，我们来思考一个问题：建立了众多的树，怎么就能够保证模型整体的效果变强呢？

集成的目的是为了模型在样本上能表现出更好的效果，所以对于所有的提升集成算法，每构建一个评估器，集成模型的效果都会比之前更好。也就是随着迭代的进行，模型整体的效果必须要逐渐提升，最后要实现集成模型的效果最优。

从数据下手

我们训练模型之前，必然会有一个巨大的数据集。我们都知道树模型是天生过拟合的模型，并且如果数据量太过巨大，树模型的计算会非常缓慢，因此，我们要对我们的原始数据集进行有放回抽样（bootstrap）。

有放回随机抽样：
有放回的抽样每次只能抽取一个样本，若我们需要总共N个样本，就需要抽取N次。每次抽取一个样本的过程是独立的，这一次被抽到的样本会被放回数据集中，下一次还可能被抽到，因此抽出的数据集中，可能有一些重复的数据。
在这里插入图片描述

在无论是Bagging还是Boosting的集成算法中，有放回抽样都是我们防止过拟合，让单一弱分类器变得更轻量的必要操作

对比随机森林：

随机森林类中也有名为boostrap的参数来帮助我们控制这种随机有放回抽样。
同时，这样做还可以保证集成算法中的每个弱分类器（每棵树）都是不同的模型，基于不同的数据建立的自然是不同的模型，这是随机森林的精华！
注意：集成一系列一模一样的弱分类器是没有意义的

在梯度提升树中，我们每一次迭代都要建立一棵新的树，因此我们每次迭代中，都要有放回抽取一个新的训练样本。不过，这并不能保证每次建新树后，集成的效果都比之前要好。

因此我们规定，在梯度提升树中，每构建一个评估器，都让模型更加集中于数据集中容易被判错的那些样本。

权重的迭代更新：

第二次以后的有放回抽样抽样中，我们加大了被第一棵树判断错误的样本的权重。也就是说，被第一棵树判断错误的样本，更有可能被我们抽中。
新建的决策树就会更加倾向于这些权重更大的，很容易被判错的样本。

采样的弊端：

采样会减少样本数量，而从学习曲线来看样本数量越少模型的过拟合会越严重，因为对模型来说，数据量越少模型学习越容易，学到的规则也会越具体越不适用于测试样本。所以subsample参数通常是在样本量本身很大的时候来调整和使用
样本量少且过拟合，正常来说样本量越大，模型才不容易过拟合，现在展现出来的效果，是由于我们的样本量太小造成的一个巧合

eta

在这里插入图片描述

针对上面提到的迭代优化过程，有以下几个问题？

如果新建的树在判断困难样本这件事上还没有前面的树做得好呢？
如果我新建的树刚好是一棵特别糟糕的树呢？

所以，除了保证模型逐渐倾向于困难样本的方向，我们还必须控制新弱分类器的生成，我们必须保证，每次新添加的树一定得是对这个新数据集预测效果最优的那一棵树。

问题实质上是一个最优化问题，如何直接求解最优的集成算法结果？

在这里插入图片描述
在 k次迭代后，我们的集成算法中总共有 k棵树，而我们前面讲明了，k 棵树的集成结果是前面所有树上的叶子权重的累加 $\sum_k^Kf_k(x_i)$ 。所以我们让棵树的集成结果 $y_i^{(k)}$ 加上我们新建的树上的叶子权重 $y_i^{(k+1)}$ ，就可以得到第k+1次迭代后，总共棵树的预测结果了。我们让这个过程持续下去，直到找到能够让损失函数最小化的 $y$ ，这个 $y$ 就是我们模型的预测结果。

参数可以迭代，集成的树林也可以迭代，万事大吉！

xgb的迭代公式：
在这里插入图片描述
其中 $\eta$ 读作"eta"，是迭代决策树时的步长（shrinkage），又叫做学习率（learning rate）。

$\eta$ 越大，迭代的速度越快，算法的极限很快被达到，有可能无法收敛到真正的最佳。 $\eta$ 越小，越有可能找到更精确的最佳值，更多的空间被留给了后面建立的树，但迭代速度会比较缓慢。
在这里插入图片描述

步长还是一个对模型效果影响巨大的参数，如果设置太大模型就无法收敛（可能导致 $R^2$ 很小或者MSE很大的情况），如果设置太小模型速度就会非常缓慢，但它最后究竟会收敛到何处很难由经验来判定

booster

选择弱评估器

在XGB中，除了树模型，我们还可以选用线性模型，比如线性回归，来进行集成。虽然主流的XGB依然是树模型，但我们也可以使用其他的模型。基于XGB的这种性质，我们有参数“booster"来控制我们究竟使用怎样的弱评估器
在这里插入图片描述

objective

在这里插入图片描述

xgb算法是传统损失函数 + 模型复杂度
在这里插入图片描述

可以用偏差和方差的角度解释，Obj的第一项是偏差，表示模型预测的精度，第二项是方差，表示模型的稳定性

其中 i代表数据集中的第 i个样本， m表示导入第棵树的数据总量， K代表建立的所有树(n_estimators)

第一项代表传统的损失函数，衡量真实标签与预测值之间的差异
第二项代表模型的复杂度，使用树模型的某种变换 $$表示，这个变化代表了一个从树
的结构来衡量树模型的复杂度的式子
注意，我们的第二项中没有特征矩阵 $X_i$ 的介入。我们在迭代每一棵树的过程中，都最小化来力求获取最优的，因此我们同时最小化了模型的错误率和模型的复杂度，这种设计目标函数的方法不得不说实在是非常巧妙和聪明。

目标函数的推导

这是迭代优化过程中的目标函数，表示每个的预测误差的累加和
分别对这两项进行展开
$g_i$ 和 $h_i$ 分别是对 $y_i^{t-1}$ 的一阶导数和二阶导数（泰勒展开式时二阶展开）
所以GBDT和XGB的区别之中，GBDT求一阶导数，XGB求二阶导数，这两个过程根本是不可类比的。XGB在求解极值为目标的求导中也是求解一阶导数

最终损失函数： $g_i$ 和 $h_i$ 只和损失有关， $f_t$ 和树有关
在这里插入图片描述

alpha, lambda

在普通的梯度提升树GBDT中，我们是不在目标函数中使用正则项的。

但XGB借用正则项来修正树模型天生容易过拟合这个缺陷，在剪枝之前让模型能够尽量不过拟合。

在这里插入图片描述

优化过程

用两张图对比理解一下：

第一张图，把梯度项中的g和h（一阶和二阶导数）进行拆解

在这里插入图片描述

gamma

$\gamma$ 的含义，增加一片叶子就会被减去的惩罚项，叶子增加的越多，惩罚越重，所以 $\gamma$ 是用来防止过拟合的重要参数

效果不亚于，n_estimator和max_depth

xgb中规定，只要结构分数之差大于0，就说明目标函数还能继续减小，就允许树继续分支
在这里插入图片描述

所以它用来停止生长

梯度回归树概念

xgboost属于梯度提升型的，即boost型的。
- 逐一构建弱评估器（准确率不低于50%的任意模型），经过多次迭代逐渐累积多个弱评估器的方法，前后关联
- 梯度提升树中可以有回归树和分类树，都以CART树算法为主流，xgboost也是

梯度提升回归树是专注于回归的树模型的提升集成模型，其建模过程大致如下：

最开始先建立一棵树
然后逐渐迭代，每次迭代过程中都增加一棵树
逐渐形成众多树模型集成的强评估器。

对于决策树而言，每个被放入模型的任意样本最终一个都会落到一个叶子节点上。
对于回归树，每个叶子节点上的值是这个叶子节点上所有样本的均值。

在这里插入图片描述

而对于梯度上升的回归树，每个样本的预测结果可以表示为所有树上的结果的加权求和

在这里插入图片描述
值得注意的是，XGB作为GBDT的改进，在上却有所不同。

对于XGB来说，每个叶子节点上会有一个预测分数（prediction score），也被称为叶子权重，这个叶子权重就是所有在这个叶子节点上的样本在这一棵树上的回归取值，用 $f_k(x_i)$ 或者 $w$ 来表示，其中 $f_k$ 表示第 k棵决策树，表示样本 $x_i$ 对应的特征向量

当有多棵树的时候，集成模型的回归结果就是所有树的预测分数之和，假设这个集成模型中总共有棵决策树，则整个模型在这个样本上给出的预测结果为：
在这里插入图片描述

叶子权重的理解

$\sum（样本值 * 叶子权重）$

在这里插入图片描述

当有多棵树的时候，集成模型的回归结果就是所有树的预测分数之和

在这里插入图片描述

然而在一个叶子节点上的所有样本所对应的叶子权重是相同的，但是随着深度和叶子数的增多，给一样的权重显然是不行的，所以引入正则化项

在这里插入图片描述

XGB 和 GBDT 的核心区别

在这里插入图片描述

训练调参

在机器学习中，我们用来衡量模型在未知数据上的准确率的指标，叫做泛化误差（Genelization error），泛化误差越小，模型就越理想.

一个集成模型(f)在未知数据集(D)上的泛化误差 $E (f; D)$ ，由方差(var)，偏差(bais)和噪声(ε)共同决定。
- 偏差就是训练集上的拟合程度决定
- 方差是模型的稳定性决定
- 噪音是随机不可控的。

过拟合情况下：调 $\gamma,\eta,\lambda, subsample,maxdepth$

调参优先级： $n e t ima t ors, e t a$ , $g amma, ma x d e pt h$ ,subsample ， $\lambda$

样本不平衡问题

存在分类，就会存在样本不平衡问题带来的影响，XGB中存在着调节样本不平衡的参数scale_pos_weight，这个参数非常类似于之前随机森林和支持向量机中我们都使用到过的class_weight参数

在这里插入图片描述

总结：

首先，XGB中的树的数量决定了模型的学习能力，树的数量越多，模型的学习能力越强。只要XGB中树的数量足够了，即便只有很少的数据，模型也能够学到训练数据100%的信息，所以XGB也是天生过拟合的模型。但在这种情况下，模型会变得非常不稳定。
第二，XGB中树的数量很少的时候，对模型的影响较大，当树的数量已经很多的时候，对模型的影响比较小，只能有微弱的变化。
- 当数据本身就处于过拟合的时候，再使用过多的树能达到的效果甚微，反而浪费计算资源。当唯一指标或者准确率给出的n_estimators看起来不太可靠的时候，我们可以改造学习曲线来帮助我们。
第三，树的数量提升对模型的影响有极限，最开始，模型的表现会随着XGB的树的数量一起提升，但到达某个点之后，树的数量越多，模型的效果会逐步下降，这也说明了暴力增加n_estimators不一定有效果。
这些都和随机森林中的参数n_estimators表现出一致的状态。在随机森林中我们总是先调整n_estimators，当n_estimators的极限已达到，我们才考虑其他参数，但XGB中的状况明显更加复杂，当数据集不太寻常的时候会更加复杂。这是我们要给出的第一个超参数，因此还是建议优先调整n_estimators，一般都不会建议一个太大的数目，300以下为佳。