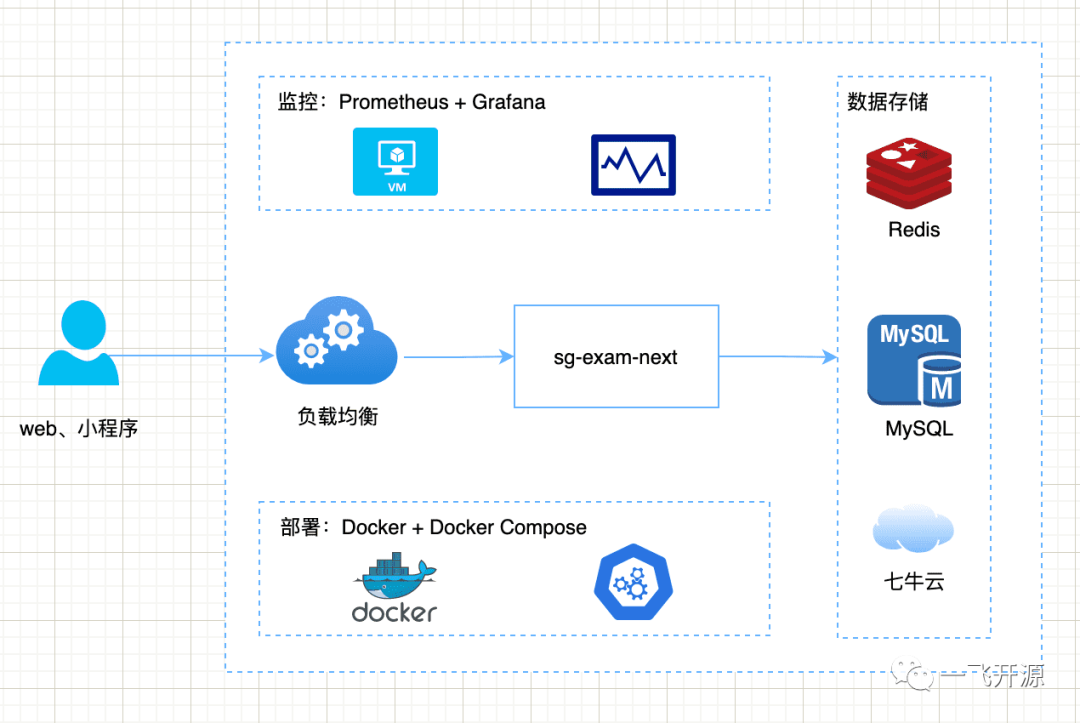
很久之前就就听说了元胞自动机（cellular automata，CA），但是一直没有尝试。得知2023年美赛春季赛只有两道赛题的时候，怕考到这个，所以出一篇元胞自动机的博客，权且当一篇学习笔记。

尝试过后才发现元胞自动机其实并没有那么难，非常好理解，算是万金油的模拟算法，可以作为保底的plan B。

1 原理介绍

1.1 概念

元胞：模拟的时候就是一个有记忆存储状态功能的格子，是元胞自动机的最基本的组成部分。因此元胞具有以下3个特点：

1. 元胞自动机最基本的单元。
2. 元胞有记忆贮存状态的功能。
3. 所有元胞状态都按照元胞规则不断更新。

状态：每个元胞都有自己的状态，随着时间的推移，状态也会改变。

元胞空间：元胞分布在空间中的格点，可以是1维、2维或n维。

邻居：能影响元胞下一时刻状态的周围元胞。一般来说有三种邻居模式（图是2维情况下的）：

当然还有其他的邻居模式，不赘述，主要看题目要求。

边界：整个元胞空间不是无穷大的，是需要一个边界范围的。边界也有好几种类型：固定型、周期型、绝热型、映射型……，个人感觉最后还是得看需要解决的问题，具体问题具体分析。

规则：根据元胞自身及邻居元胞的状态，决定下一时刻元胞状态的决定，可以是动力学函数或状态转移方程。

1.2 原理

这个没啥原理，这部分简单讲讲步骤：

Step1：建立假设、简化条件。

Step2：设置初始状态和边界。

Step3：推导状态转方程和条件。

Step4：根据时间迭代。

基于大量的实验，人们发现元胞自动机根据动力学行为能分为 4 类（Wolfram. S.，1986)：

1. 平稳型：自任何初始状态开始，经过一定时间运行后，元胞空间趋于一个空间平稳的构形，这里空间平稳即指每一个元胞处于固定状态。不随时间变化而变化。
2. 周期型：经过一定时间运行后，元胞空间趋于一系列简单的固定结构（Stable Patterns）或周期结构（Perlodical Patterns)。由于这些结构可看作是一种滤波器（Filter），故可应用到图像处理的研究中。
3. 混沌型：自任何初始状态开始，经过一定时间运行后，元胞自动机表现出混沌的非周期行为，所生成的结构的统计特征不再变止，通常表现为分形分维特征。
4. 复杂型：出现复杂的局部结构，或者说是局部的混沌，其中有些会不断地传播。

我们不对每种类型的元胞做实验验证，只提供几种经典和常见的例子。

2 实例

2.1 奇偶游戏

条件：

1. 邻居和为奇数时，中间的数字变成1；
2. 邻居和为偶数时，中间的数字变成2。

%%奇偶规则游戏
clear;clc;
n = 1000;%指定边界长度
Se = zeros(n);
z = zeros(n);
Se(n/2-2:n/2+2,n/2-2:n/2+2)=1;  %初始化中间的点
Ch = imagesc(Se);
axis square;
Sd = zeros(n+2);  %边界
while(true) %死循环
    % 保存现有状态的右2：边界1，右边1
    Sd(2:n+1,2:n+1) = Se;
    % 上下左右加一次
    sumValue = Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2);
    % 摸一下
    Se = mod(sumValue,2);
    set(Ch,'cdata',Se);
    pause(0.0001)
end

9倍速效果如下

还挺好看的

不是个实际例子，但是可以看出元胞自动机的代码模板，反正就是这么一个流程。

2.2 生灭游戏

条件：

1. 如果活细胞周围活细胞数小于2个或者大于3个，则转为死；
2. 如果活细胞周围活细胞数为2个或者3个，则保持活；
3. 如果死细胞周围有3个活细胞，则转为活。

对于活细胞，我们用1表示；对于死细胞，我们用0表示。

n = 200;
p = 0.4;
z = zeros(n);
Se = rand(n)<p;
Sd = zeros(n+2);
Ph = imagesc(Se);
while(true)
    Sd(2:n+1,2:n+1)=Se;
    sumValue = Sd(1:n,1:n)+Sd(1:n,2:n+1)+Sd(1:n,3:n+2)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2)+Sd(3:n+2,1:n)+Sd(3:n+2,2:n+1)+Sd(3:n+2,3:n+2);
    for i=1:n
        for j=1:n
            if(sumValue(i,j)==3||(sumValue(i,j)==2&&Se(i,j)==1))
                Se(i,j) = 1;
            else
                Se(i,j) = 0;
            end
        end
    end
    set(Ph,'cdata',Se);
    pause(0.05);
end

二倍速效果如下：

丑丑的

最后趋于平衡了

2.3 森林火灾

条件：

1. 对于树木：它可能会被雷劈，导致树木着火变成火树；它可能会被附近的火树点着，变成火树；也可能保持现状
2. 对于火树：它可能会烧成灰，变成空地；也可能会继续烧，保持现状
3. 对于空地：它可能会长出树木，变成树；也可能保持现状
4. 对于火树传播：火树附近1格的树有概率变成火树

各种概率简单起见我自己定了，如果是比赛，可能需要假设和计算概率方程。

2.3.1 普通森林大火

此时我们不考虑其他因素，简单地将火烧成空地的概率定位0.5，树被雷劈的概率定义为0.000001，空地长树的概率定为 0.01，树被旁边火烧到的概率定为0.7。

clear;clc;
%火灾
n = 300;                           % 定义表示森林的矩阵大小
k = 30000;                         % 迭代次数
Pground = 0.2;                     % 从着火变成空地的概率
Plight = 1e-6; Pgrowth = 2e-3;      % 定义闪电和生长的概率  
P2=0.7; %旁边有火，树着火的概率
% UL = [n,1:n-1]; DR = [2:n,1];      % 定义上左，下右邻居
veg=zeros(n,n)+2;                    % 初始化表示森林的矩阵
imh = image(cat(3,veg,veg,veg));   % 可视化表示森林的矩阵
Sd = zeros(n+2);                 %边界
% veg = 空地为0 着火为1 树木为2
for i=1:k
    Sd(2:n+1,2:n+1) = veg;
    sumValue = (Sd(1:n,2:n+1)==1)+(Sd(2:n+1,1:n)==1)+(Sd(2:n+1,3:n+2)==1)+(Sd(3:n+2,2:n+1)==1);
    for p=1:n
        for q=1:n
            if(veg(p,q)==2 && ((sumValue(p,q)>0 && rand()<P2)||rand()<Plight))
                %首先要是树，而且需要邻居有火，就会一定概率着火;或者被雷劈了,就会直接着火
                veg(p,q)=1;
            elseif(veg(p,q)==1&&rand()<Pground)
                %如果是火且满足概率，则变为空地
                veg(p,q) = 0;
            elseif(veg(p,q)==0&&sumValue(p,q)==0&&rand()<Pgrowth)
                %如果是空地，且周围没有火，那么以一定概率长成树
                veg(p,q) = 2;
            end
        end
    end
    set(imh, 'cdata', cat(3,(veg==1),(veg==2),zeros(n)))
    drawnow  
end

7倍速效果如下图

还是能看出来森林大火和树生长维持动态平衡的。

2.3.2 东风森林大火

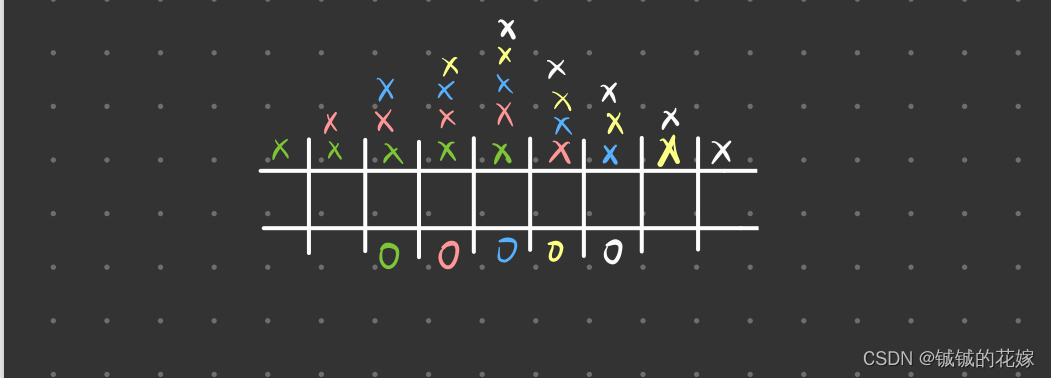
如上图所示，如果是北风，不同颜色的火树（圆圈）对风方向2格的树木的影响是这样的（X代表是否会被火树影响）。可以看出传播方向越边缘的树，越难被火树波及，在火树林正前方的树很容易被点着。

其实没难多少，就是加了个判断和概率，计算的时候再算一下吹风的时候会按照风的方向影响2格的树木，这个已经写在代码注释中了~~

clear;clc;
%火灾
n = 300;                           % 定义表示森林的矩阵大小
k = 30000;                         % 迭代次数
Pground = 0.2;                     % 从着火变成空地的概率
Plight = 1e-6; Pgrowth = 2e-3;      % 定义闪电和生长的概率  
Windposb = 2e-1;                    % 定义风的效果
P2=0.7;                             %旁边有火，树着火的概率
veg=zeros(n,n)+2;                    % 初始化表示森林的矩阵
imh = image(cat(3,veg,veg,veg));   % 可视化表示森林的矩阵
Sd = zeros(n+4);                 %边界
% veg = 空地为0 着火为1 树木为2
for i=1:k
    Sd(3:n+2,3:n+2) = veg;
    % 周围有火
    sumValue = (Sd(2:n+1,3:n+2)==1)+(Sd(3:n+2,2:n+1)==1)+(Sd(3:n+2,4:n+3)==1)+(Sd(4:n+3,3:n+2)==1);
    sumWindValue = (Sd(1:n,5:n+4)==1)+(Sd(2:n+1,5:n+4)==1)+(Sd(3:n+2,5:n+4)==1)+(Sd(4:n+3,5:n+4)==1)+(Sd(5:n+4,5:n+4)==1);
    for p=1:n
        for q=1:n
            if(veg(p,q)==2 && ((sumValue(p,q)>0 && rand()<P2)||rand()<Plight||(rand()<Windposb && sumWindValue(p,q)>0)))
                %首先要是树，而且需要邻居有火，就会一定概率着火;或者被雷劈了,就会直接着火;或者是东风让东火烧到了
                veg(p,q)=1;
            elseif(veg(p,q)==1&&rand()<Pground)
                %如果是火且满足概率，则变为空地
                veg(p,q) = 0;
            elseif(veg(p,q)==0&&sumValue(p,q)==0&&rand()<Pgrowth)
                %如果是空地，且周围没有火，那么以一定概率长成树
                veg(p,q) = 2;
            end
        end
    end
    set(imh, 'cdata', cat(3,(veg==1),(veg==2),zeros(n)))
    drawnow  
end

5倍速效果如下

3 小结

感觉原理和实现方面，元胞自动机应该没什么难度，其实可能在知道元胞自动机这个概念之前有的读者就已经有意识无意识地去做类似的操作了，元胞自动机实际上就只是给这些操作外面套一个好听的名字罢了。

个人感觉元胞自动机的难点和重点并不在于实现和模型可能以下两点相对更重要一点：

1. 假设

以森林大火为例，难点在怎么根据题意建立元胞自动机模型吗？或许难度有那么一丢丢，但是显然不是重点。个人感觉说清楚各个参数的取值的原因，甚至为这些参数的设定建立一些系数公式（例如，风速x怎么影响火蔓延速度g(x)的），也非常重要。

除此之外，假设也是需要考虑的一点。说到底元胞自动机还是比较简单的没怎么考虑其他现实条件的抽象数学模型，很多实际因素都被忽略了、被简化了，这个是需要说清楚的。事实上，模型的优化和题目的推进往往就是建立在让数学模型不断接近现实条件的基础上的，即一点一点加入被考虑的因素和条件，让模型变得更全面。

2. 模型优化

简单的元胞自动机谁都会，作为一篇优秀的数模论文，在模型方面显然不能只用最简单的模型的拼凑和堆叠，如果可以，当然是优化后的模型更香。不过这种东西显然有点可遇不可求，如果前期没有相应的准备，赛中做这个的时候一定要保证时间充足。

如果调研过，就会发现其实现在很多论文都已经提出了元胞自动机组合优化模型，比如神经网络 + 元胞自动机或者是元胞自动机 + 多智能体的模型。