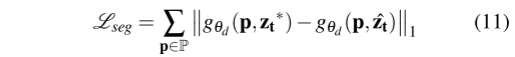2010 MDM

1 ST-matching的问题

论文笔记：Map-Matching for low-sampling-rate GPS trajectories（ST-matching）_UQI-LIUWJ的博客-CSDN博客

当轨迹很长，且车辆通过多线平行的道路时，ST-Matching的效果较差，出现Z形结果的明显错误

 

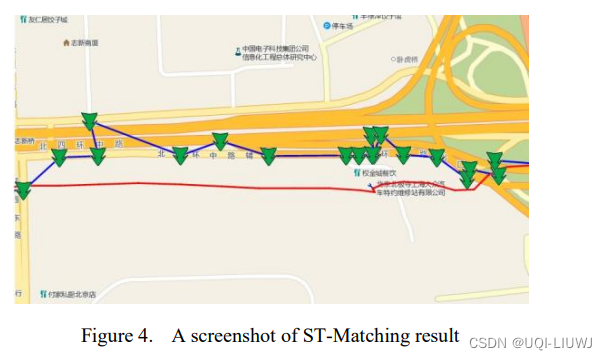
 【我的理解：ST-matching在计算空间分析函数的时候，虽然使用的是两个candidate点之间的路径距离，但是在得到candidate以还原轨迹的时候，是直接把最可能的candidate连起来的，所以会出现横穿北四环的情况】

出现这种错误的原因是

• 计算相似时仅考虑相邻候选点，而实际上应当考虑所有附近的点。
• 权重打分使用简单的求和，忽略了距离的影响。
• 如果一个点被错分了，那么后续的节点都会基于此计算，造成误差累计。

——>论文提出了IVMM，通过voting的方式，综合考虑所有的采样点之间的关系，以找到最优路径

2 IVMM算法

2.1 构建候选点图

2.1.0 获得候选点

这一步和ST-matching一样：

• 给定一条确定轨迹
• 对每一个点pi​，在半径为r的范围内搜索该路段的候选集
• 然后计算候选点，候选点是pi​对这些路段的投影

 

 

 

 2.1.1 构建候选点图

这一步也是和ST-matching一样，每两个candidate之间的边权重为：

 详细内容可见：论文笔记：Map-Matching for low-sampling-rate GPS trajectories（ST-matching）_UQI-LIUWJ的博客-CSDN博客

 

2.2 不同采样点之间的转移关系

这里开始就和ST-matching不一样了

2.2.1 static score matrix

candidate的状态转移概率矩阵按对角矩阵拼起来得到

• 
  • 其中 ，也就是相邻两个采样点i-1和i中各个candidate之间的转移概率矩阵
• 

 2.2.2 Weighted Influence Modeling

• 为每个采样点p定义一个(n-1)维的距离权重(对角)矩阵Wi，表示点p与其他采样点间的权重关系
• 权重关系用欧式距离表示，距离越大权重越小。
• 

 2.2.3 Weighted Score Matrix

• Static score matrix M可以看成一个由n-1个block组成的对角矩阵
• 每一个采样点的距离权重矩阵Wi也是一个n-1阶对角矩阵
• wi的每个元素和M对应block的每个元素相乘，得到weighted score matrix：

   

  • 
• Φi表示从采样点pi的视角看，各个candidate之间的加权转移概率
  • 距离采样点pi越近的点，权重越大，表示从pi视角看，影响（可信度）越大
• ——>得到一组共n个加权得分矩阵，表示从不同采样点的视角下看，各个转移概率的情况

 

2.3 VIMM算法

 

 

 2.4 举例

不用VIMM的时候，路线就是1112

 

 

 VIMM voting之后，路径为1123

3 实验

3.1 实验数据

真实数据和st-matching一样，都是北京的数据 

• 北京的路网
  • 58624个点
  • 130714条路段
• 

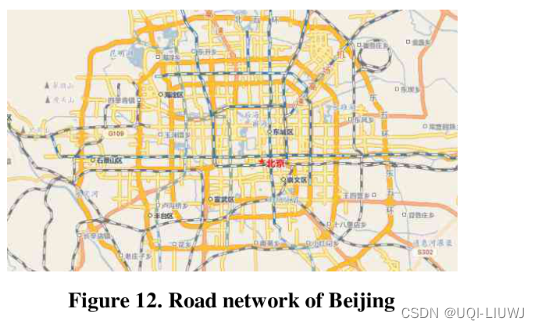
• 真实数据
  • 从GoeLife系统中采集26条轨迹，这些轨迹都手工标注的label（作为ground truth
  • 

   

 3.2 比较的metric

 

 3.3 结果

3.3.1 可视化结果

 

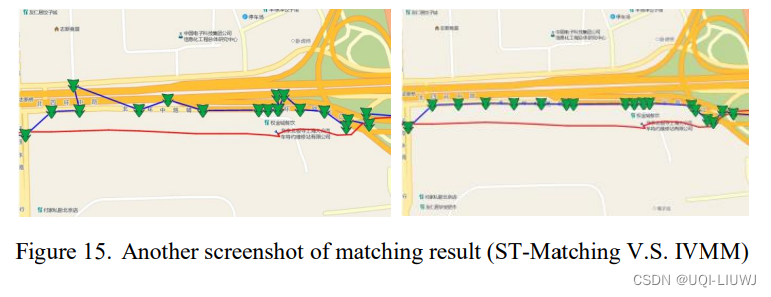
 3.3.2 准确度