【中级软件设计师】—(针对上午题)算法分析与设计(三十八)


一、回溯法
1. 什么是回溯法?
相信"迷宫"是许多人儿时的回忆,大家小时候一定都玩过迷宫游戏。我们从不用别人教,都知道走迷宫的策略是:
当遇到一个岔路口,会有以下两种情况:
存在没走过的路。此时可以任意选一条没走过的路深入,只要记住我们所走过的路径即可。
倘若下次再来到这个路口,便不再沿着走过的路径继续深入,而是沿着没走过的路径深入下去;
所有路都已经走过。如果所有岔路口都已经遍历,则回退至上一个最近的岔路口。
当遇到死胡同,便回退到刚才距离最近的岔路口。
不断前进并重复该过程,直到找到终点或回退到起点位置。
其实,这就是回溯法:一个基于深度优先搜索和约束函数的问题求解方法。
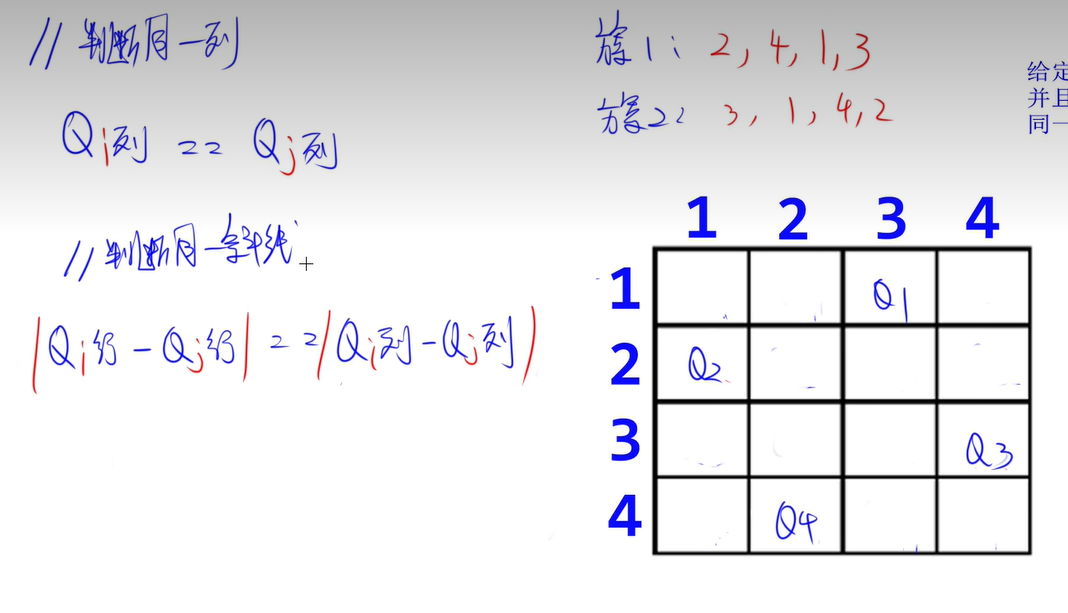
(1)、n皇后问题

📢 非递归求解n皇后问题
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define N 4
int q[N + 1]; // 存储皇后的列号
int check(int j)
{ // 检查第i个皇后的位置是否合法
int i;
for (i = 1; i < j; i++)
{
if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j]))
{ // 判断是否在同一斜线上
return 0;
}
}
return 1;
}
void queen()
{ //
int i;
for (i = 1; i <= N; i++)
{
q[i] = 0;
}
int answer = 0; // 方案数
int j = 1; // 表示正在摆放第j个皇后
while (j >= 1)
{
q[j] = q[j] + 1; // 让第j个皇后向后一列摆放
while (q[j] <= N && !check(j))
{ // 判断第j个皇后的位置是否合法
q[j] = q[j] + 1; // 不合法就往后一个位置摆放
}
if (q[j] <= N)
{ // 表示第j个皇后的找到一个合法的位置
if (j == N)
{ // 找到了一组皇后的解
answer = answer + 1;
printf("放案%d:", answer);
for (i = 1; i <= N; i++)
{
printf("%d", q[i]);
}
printf("\n");
}
else
{ // 继续摆放下一个皇后
j = j + 1;
}
}
else{ // 表示第j个皇后找不到一个合法的位置
q[j] = 0; // 还原第j个皇后的位置
j = j - 1; // 回溯
}
}
}
int main()
{
queen();
return 0;
}
📢 递归求解n皇后问题
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define N 4
int answer=0;
int q[N + 1]; // 存储皇后的列号
int check(int j)
{ // 检查第i个皇后的位置是否合法
int i;
for (i = 1; i < j; i++)
{
if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j]))
{ // 判断是否在同一斜线上
return 0;
}
}
return 1;
}
void queen(int j){
int i;
for(i=1;i<=N;i++){
q[j]=i;
if(check(j)){// 当摆放的皇后位置为合法时
if(j==N){//找到了N皇后的一组解
answer=answer+1;
printf("方案%d:",answer);
for(i=1;i<=N;i++){
printf("%d",q[i]);
}
printf("\n");
}else{
queen(j+1);//递归摆放下一个位置
}
}
}
}
int main()
{
queen(1);
return 0;
}

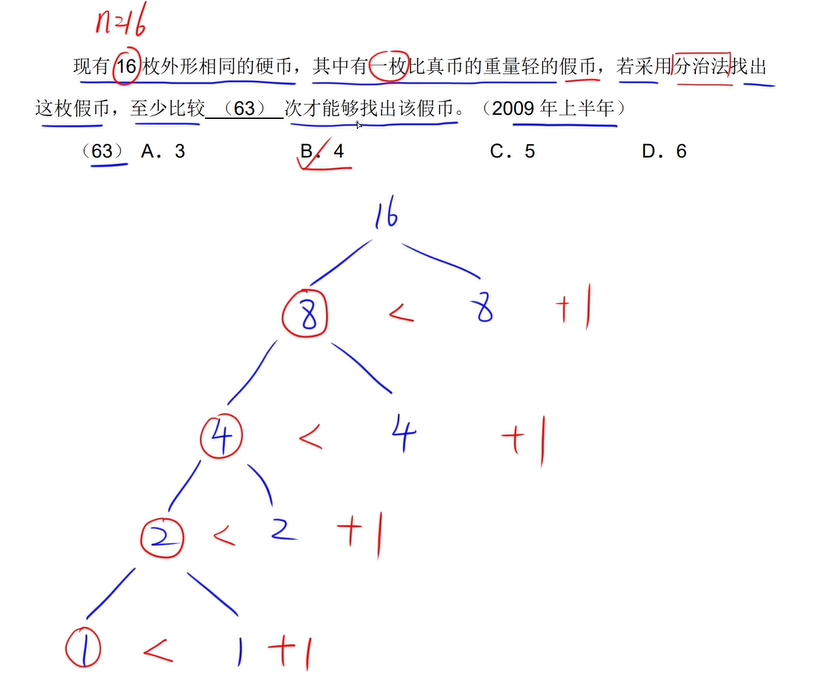
二、分治法
递归的概念


分治法的基本思想

2
3

4

5

三、动态规划
动态规划法的基本思想:


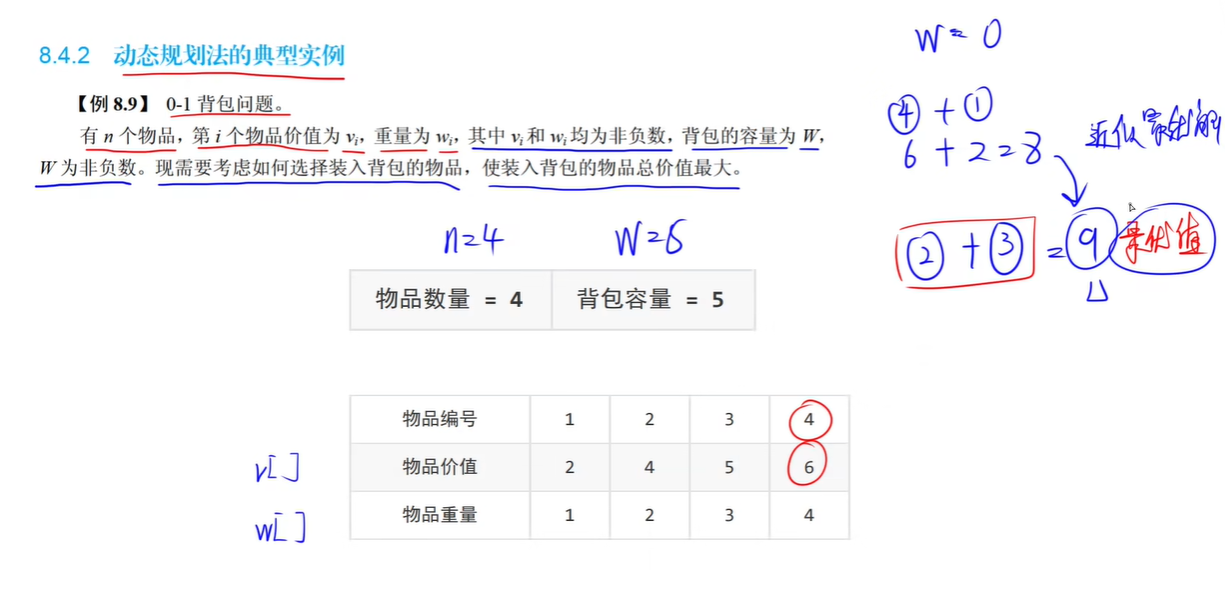
动态规划—背包问题
01背包问题
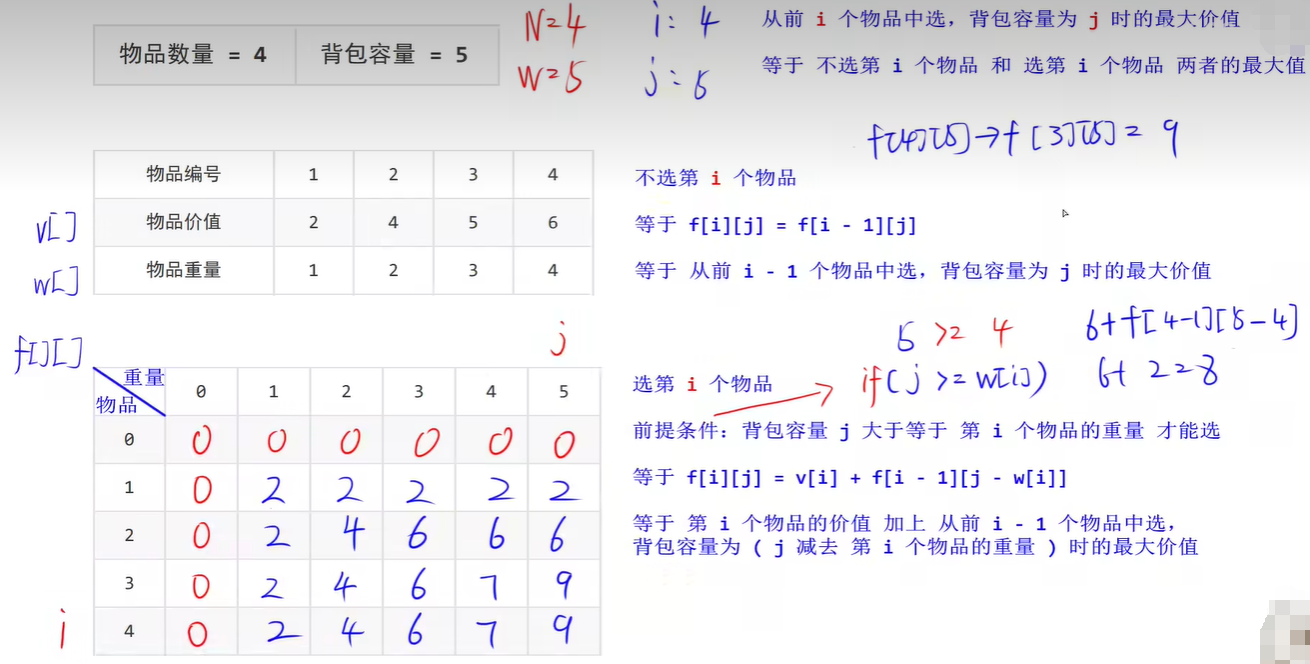
#include <stdio.h>
#define N 4 // 物品数量
#define W 5 // 背包容量
int max(int a, int b)
{
return a > b ? a : b;
}
int main()
{
int v[] = {0, 2, 4, 5, 6}; // 物品价值数组
int w[] = {0, 1, 2, 3, 4}; // 物品重量数组
int f[N + 1][W + 1] = {}; // 子问题解数组
int i, j;
for (i = 1; i <= N; i++)
{
for (j = 1; j <= W; j++)
{
f[i][j] = f[i - 1][j]; // 默认不选第i个物品
if (j >= w[i])
{ // 选第i个物品的前提条件
// 等于 不选第i个物品 和选第i个物品 两者的较大值
f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);
}
}
}
printf("%d\n", f[N][W]);
for (i = 0; i <= N; i++)
{
for (j = 0; j <= W; j++)
{
printf("%d", f[i][j]);
}
printf("\n");
}
return 0;
}
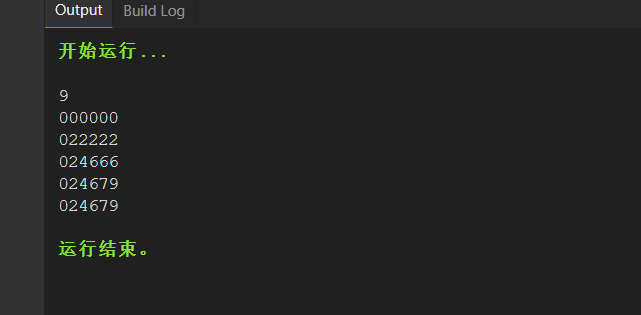
0-1背包问题时间复杂度和空间复杂度
6

7

8


9


📢矩阵相乘问题:算法策略动态规划法,时间复杂度为O(n^3),空间复杂度O(n^2)
10

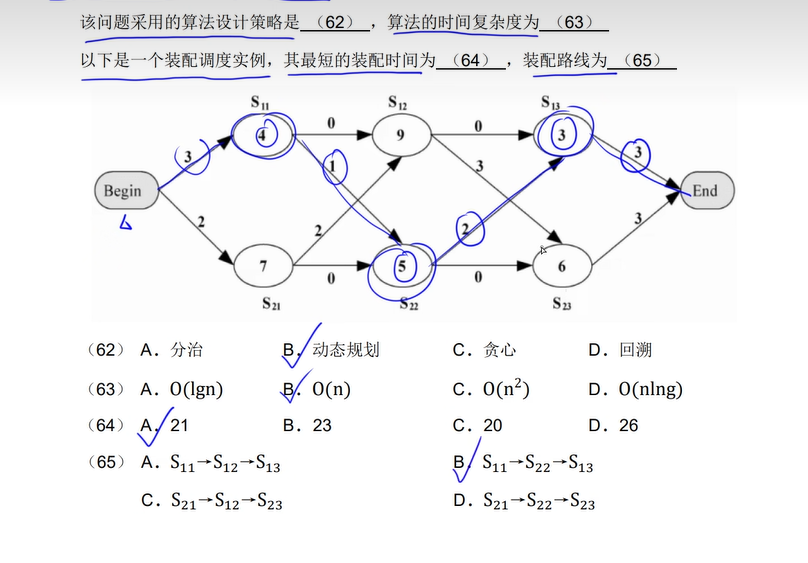
11

12

记住:


四、贪心法
贪心法的基本思想

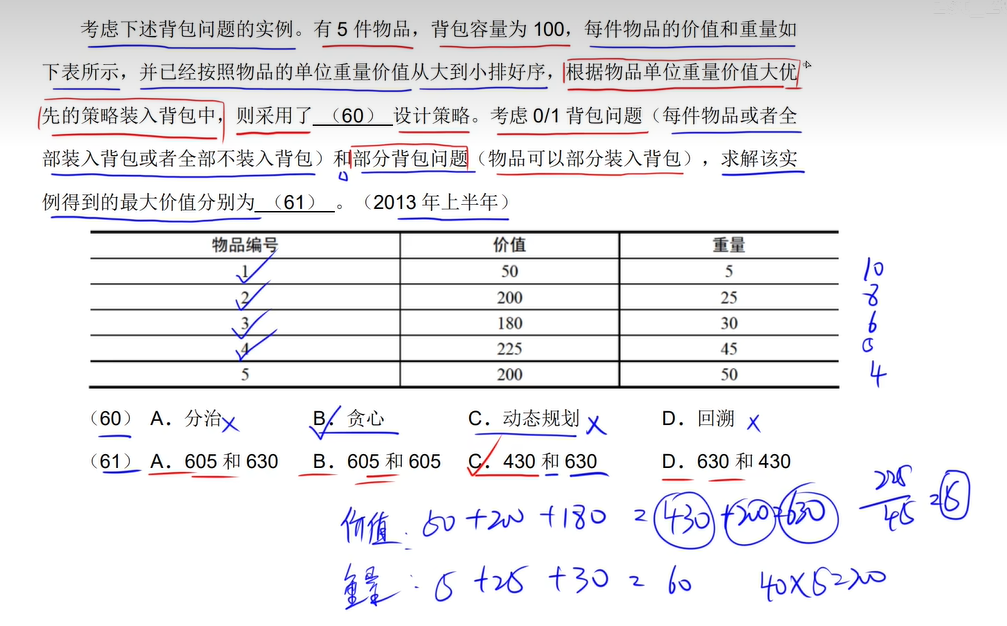
部分背包问题
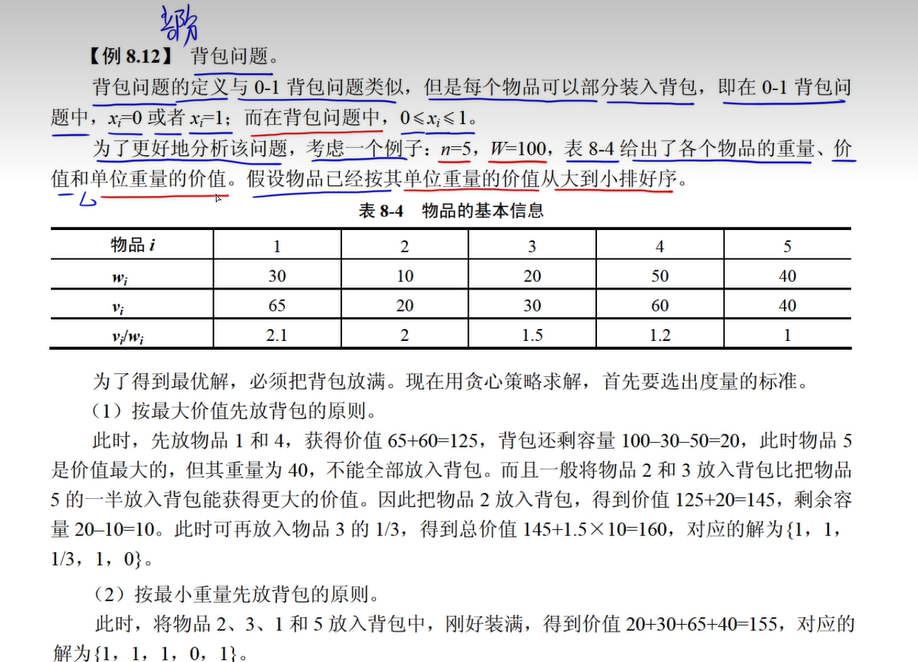

部分背包问题代码实现
13😭😭

14😭😭
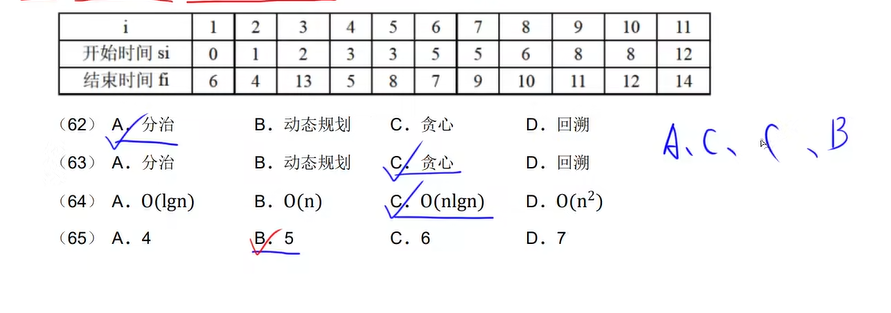
15

16
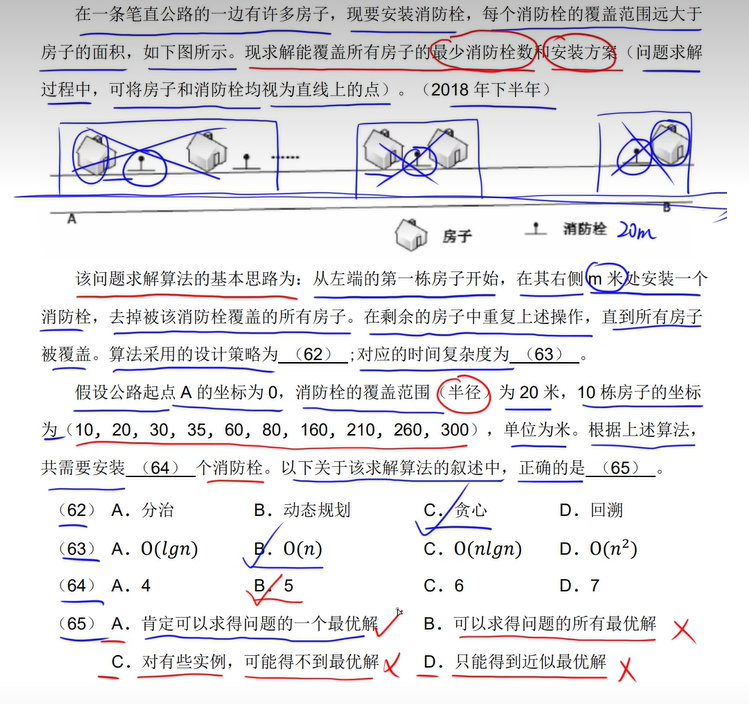
答案:C B B A,不理解的看up算法的P31个视频
五、算法总和
📢贪心法

📢📢回溯法

📢📢📢分支限界法

17

18
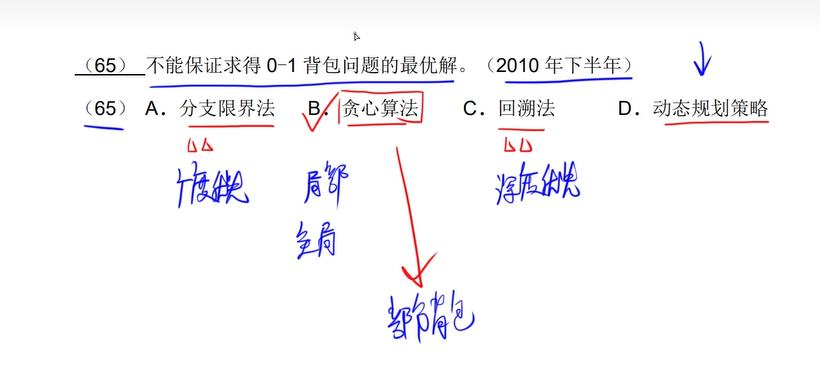
19

20

21

22





![P1038 [NOIP2003 提高组] 神经网络](https://img-blog.csdnimg.cn/img_convert/045bbba51ab9d289043296ef39f5ff17.png)