Author: Zelin Zang, Siyuan Li, Di Wu and Stan Z Li.
1-4: Westlake University

摘要

流形学习（ML, Manifold learning）旨在从高维数据中识别低维结构和嵌入，然而我们发现现有工作在采样不足的现实数据集上效果不佳。一般的ML方法对数据结构进行建模然后构造一个低维embedding，但是采样不足的现实数据会导致局部关联性/连续性较差，或由于优化目标不合适导致结构失真、embedding存在缺陷。为解决该问题我们提出了深度的、局部平坦的、流形embedding（DLME）：通过减少失真来获得可靠的embedding。该方法通过数据增强构建语义流形、借助局部平坦假设克服结构失真问题，并设计了一个新的损失，在数学上证明了局部平坦假设能够得到理想的embedding。实验表明我们的方法在下游分类聚类任务中优于SOTA方法，也优于对比学习方法。

1. Introduction

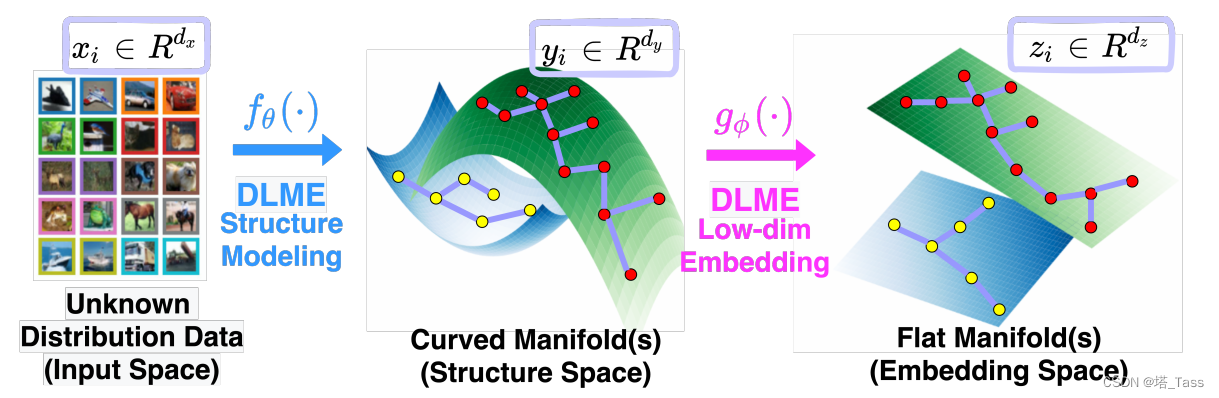
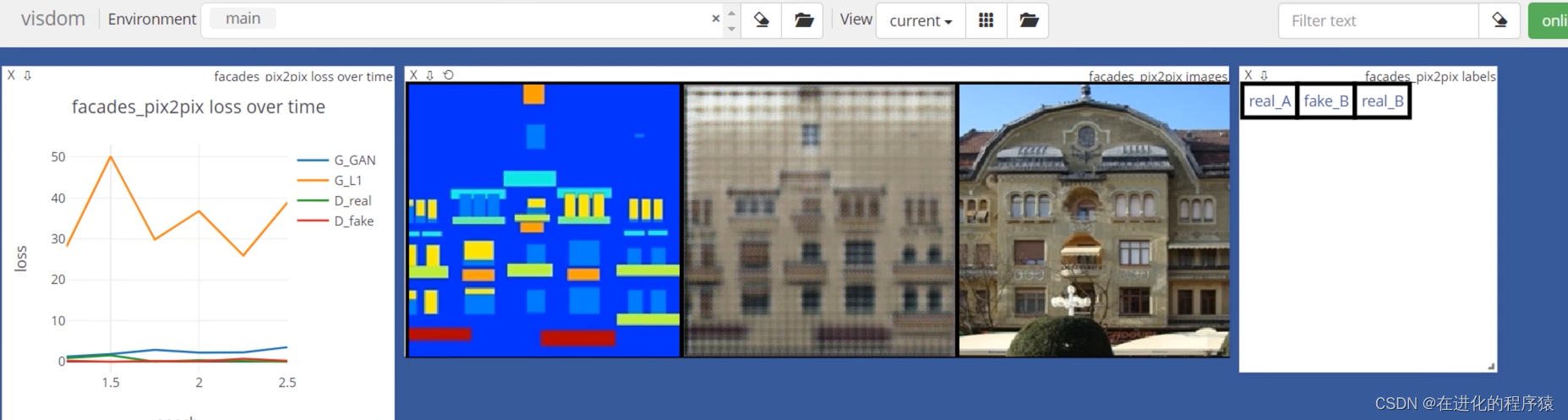
图1：我们的DLME包括了结构建模网络$f_{\theta }$和低维嵌入网络$g_{\varphi }$。前者将输入数据映射到可以描述数据连接的结构空间中，后者再利用局部平坦特性将卷曲的流形映射到平面嵌入空间中，以对下游任务友好并提升可辨别能力。

我们将目前的流形学习方法的问题总结为：

• D1: 对流形嵌入的约束不足
  专注于局部结构的关系容易产生扭曲失真的嵌入，从而影响下游任务的执行，如图2（D2）和图6所示。由于对潜在特征空间的约束不足，即使是最先进的ML方法在下游任务上也会失去性能，如对比学习。

• D2: 流形结构失真
  我们将现有方法在现实数据集上的问题归因于结构失真：现有ML方法使用输入空间中的距离来构建局部近邻图，据此来定义可以保留局部结构的无监督损失。然而，该方法引入了一个严格的假设，即局部一定存在短程连接，使得距离度量可以描述数据的近邻关系。这通常只有数据密集时才有可能满足，而在真实数据集中并不一定能得到保证。

• D3: 局部嵌入崩溃
  最近，对比学习利用数据增广之间的相似性取得了好的性能并得到广泛关注，然而它在流形学习中遇到的了更严重的困难，因为该方法需要大量的数据进行预训练，对比学习无平滑损失导致模型学习到的特征容易局部崩溃，需要大量的数据来学习有效的知识，如图2（D3）所示。

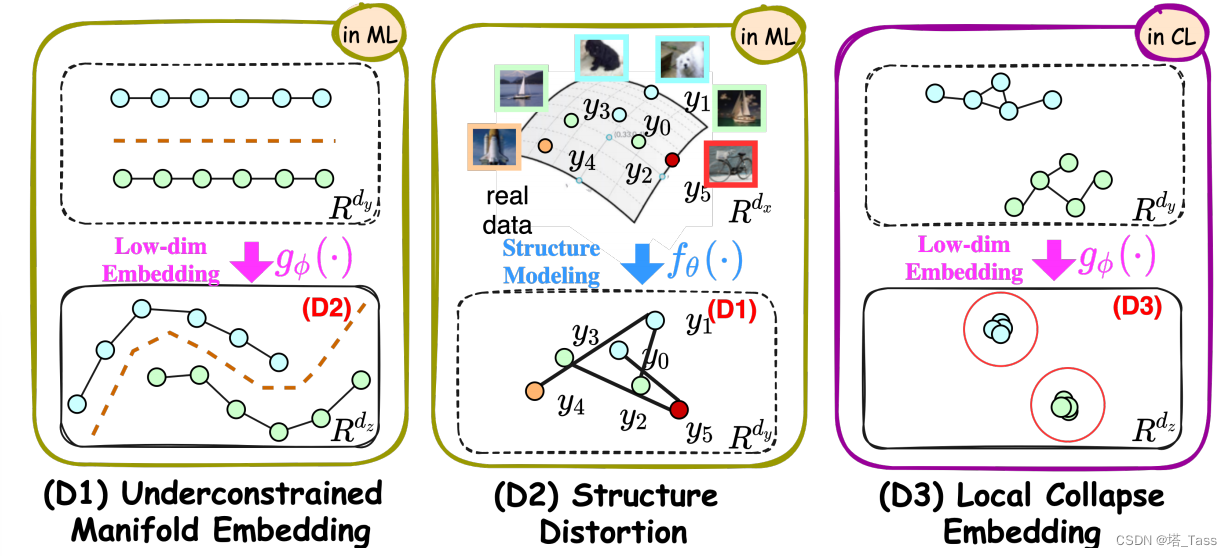
图2：传统ML和CL方法的问题。(D1)：局部视角和一阶相似性约束$\to$导致约束不足的流形嵌入；(D2)：现实数据的超高维度导致数据分布稀疏/采样不良$\to$打破流形的局部连通性$\to$导致结构失真；(D3)：对比学习非平滑的损失函数$\to$导致局部崩溃的嵌入$\to$对下游任务不友好。

在图1中，我们希望更好的限制潜在特征空间以防止出现结构失真问题，同时希望出现类似对比学习方法的崩溃嵌入问题，于是提出了一个两步走的模型结构：1）通过测量每个样本对的关系来获得流形的图结构，2）将得到的结构映射到低维平面特征空间中。具体来说，我们首先提出一种新的局部平坦假设，添加了二阶流形曲率约束来获得更合理的潜在空间（解决D1）；然后我们设计了一个与数据增广兼容的深度学习框架使得方法可以更好的训练并scale到更大数据集上（解决D2）；最后，我们根据局部平坦假设设计了一个与数据增广兼容的平滑损失函数，该函数基于长尾 t-分布来指导网络学习。我们进一步在数学上说明了为什么DLME不同与传统对比损失以及DLME为什么可以获得平面的局部嵌入。

2 Related work

略

3 Method

3.1 问题描述和局部平坦假设

定义1：流形学习
令$\mathcal{M}$为欧式空间${\mathbb{R}}^d$中的d维嵌入，$f:\mathcal{M}\to {\mathbb{R}}^D$为可微的嵌入映射，流形学习的目的是从足够的采样观测数据 X = { x i } i = 1 N X=\{x_i\}_{i=1}^N X={xi​}i=1N​中找到 Z = { z i } i = 1 N , z i ∈ M Z=\{z_i\}_{i=1}^N, z_i\in\mathcal M Z={zi​}i=1N​,zi​∈M。在我们的方法中，利用神经网络$f_{\theta }$学习该映射${\mathbb{R}}^D\to {\mathbb{R}}^d$

每个ML方法都是根据特定的流形假设设计一个损失函数，将观察到的数据$x_i$映射到内在流形$z_i$，例如，LLE假设局部流形是线性的，而UMAP假设局部流形是均匀的。对比之下，我们提出了潜在空间中的局部平坦假设。

假设1： 局部平坦假设（LFA）
我们希望每个数据点与其邻居位于局部的平坦平面上，我们引入了Gauss-Bonnet定理，使用平均曲率${\overline{K}}_{\mathcal{M}}$来量化高维流形的平坦程度：

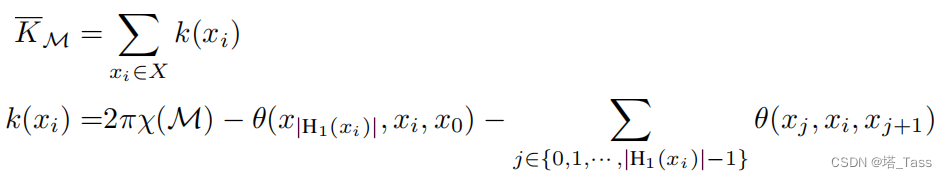
其中，$\mathcal{X}(\mathcal{M})$为欧拉特征（Euler Characteristic），${\mathrm{H}}_1$为当前数据点的1-近邻，$\theta (x_j,x_i,x_{j+1})$为这三个点的角度。

从一阶约束到二阶（曲率）约束
传统方法设计保持距离（如LLE）或保持相似性（如UMAP）的目标函数，希望在映射过程中保证数据的一阶结构关系。我们引入了二阶曲率约束来解决结构失真问题。但是二阶损失的计算复杂度十分昂贵，我们因此需要利用局部平坦假设来最小化流形embedding的曲率。这种想法类似于压缩感知中的先验稀疏性——局部平坦假设期望不受约束的局部曲率信息是稀疏的。

局部平坦假设的作用
对于单个流形：局部平坦假设减少了不合适的嵌入空间中的卷曲（如图6）从而避免了嵌入过程的失真。
对于多个流形：局部平坦假设可以简化多个流形之间的判别关系，在避免崩溃嵌入的同时减少了不同流形之间重叠的可能性，使下游任务可以通过简单的线性模型完成。

3.2 DLME框架

DLME的损失是根据$A_{ij}$和从头训练的神经网络空间中的点对相似性计算的，如果来自相同数据的增广，则$A_{ij}=1$，否则$A_{ij}=0$

利用数据增广解决结构失真。利用对比学习的思想，DLME通过数据增强提供的先验知识解决由于采样点稀疏导致的结构失真问题：由于数据增强尽可能少地改变原始数据的语义，因此当原始数据的局部连接中断时，通过数据增强可以生成孤立数据点的近邻数据，从而保证了局部连接。

DLME的前向过程：

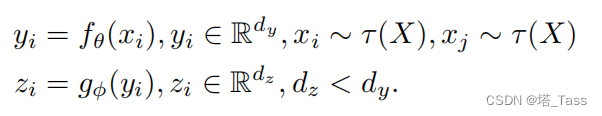
其中$x_i$和$x_j$采样自不同的随机图像增广，$d_y$和$d_z$分别为嵌入维度。

DLME的损失函数：

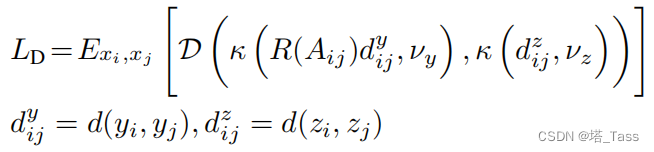
其中$d_{ij}^y,d_{ij}^z$ 为处于嵌入空间y和z中点对$(i,j)$的距离度量，双路差异度量$\mathcal{D}(p,q)$定义了两个潜在空间的不相似性：
$$\mathcal{D}(p,q)=p\log q+(1-p)\log (1-q)$$
这是连续版本的交叉熵，用于引导两个潜在空间的点对相似性以互相匹配。

由于潜在空间的维度不同，直接计算两个空间的距离存在维度不匹配的障碍。我们因此采用t-分布作为核函数来计算点对之间的相似性，从而描述数据的分布。t-分布中的自由度$v_y,v_z$是一种用于增强嵌入空间平坦度的必要设置：

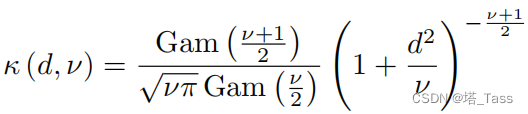
其中Gam表示Gamma函数，自由度$v$控制核函数的形状。

最后，$R(A_{ij})$将近邻信息整合到$A_{ij}$中：
$$R(A_{ij})=1+(\alpha -1)A_{ij}$$
即，当点j是点i的近邻时，在结构空间中的距离将被减少到$\alpha \in [0,1]$，否则设置为1，这两个点的相似度将会增加。

3.3 通过更平滑的对比学习框架来对抗局部崩溃

传统自监督对比学习框架可以写为：
$$L_C=-{\mathbb{E}}_{x_i,x_j}[A_{ij}\log \kappa (d_{ij}^z)+(1-A_{ij})\log \left(1-\kappa (d_{ij}^z)\right)]$$
该对比学习目标是不平滑的，因为点对的学习目标随着$A_{ij}$的变换在$\log \kappa$和$\log (1-\kappa )$之间切换。DLME降低折衷了学习过程，避免了梯度中的尖锐冲突。为了比较DLME损失和CL损失之间的差异，我们假设$g_{\phi }$满足K-Lipschitz连续性，然后：
$$d_{ij}^z=k^{\ast }{d}_{ij}^y,k^{\ast }\in [1/K,K]$$ 其中$k^{\ast }$为Lipschitz常量。那么CL损失和DLME损失的差异为：
$$|L_D-L_c|={\mathbb{E}}_{x_i,x_j}\left[A_{ij}-\kappa \left((1+(\alpha -1)A_{ij}{k}^{\ast }{d}_{ij}^z\right)\log (\frac{1}{\kappa (d_{ij}^z)}-1)\right]$$

分析上式，当$i$和$j$为近邻，$A_{ij}=1$，再当$\alpha \to 0$时，$\alpha k^{\ast }{d}_{ij}^z\to 0,1-\kappa (\alpha k^{\ast }{d}_{ij}^z)\to 0$，于是$|L_D-L_c|\to 0$，而当$\alpha >0$时，DLME的最优解保留了关于embedding结构$d_{ij}$的余数，表明我们的损失不会最大化当前点和近邻点的相似性，我们的损失相比对比损失更平滑，可以保留embedding空间中的结构（只会有轻微崩溃），而不会把近邻点都压缩到一起变成崩溃embedding空间。

3.4 为何DLME导致局部平坦面

本节讨论DLME如何优化局部曲率以变得更平坦。我们已经讨论了如何对结构建模并在利用对比学习防止局部连接不良的同时利用平滑损失防止崩溃解，但是流形依然是卷曲的，可能导致不同流形之间的重叠和变形，使得下游的线性模型性能下降。我们因此需要获得尽可能平坦的embedding空间，我们的损失可以控制embedding空间的平坦程度。这是因为损失函数中的基于长尾t-分布的核函数，我们在两个潜在空间中应用不同的自由度参数，自由度$v_y$和$v_z$的差异形成了不同的核函数$\kappa (d,v_y)$和$\kappa (d,v_z)$。

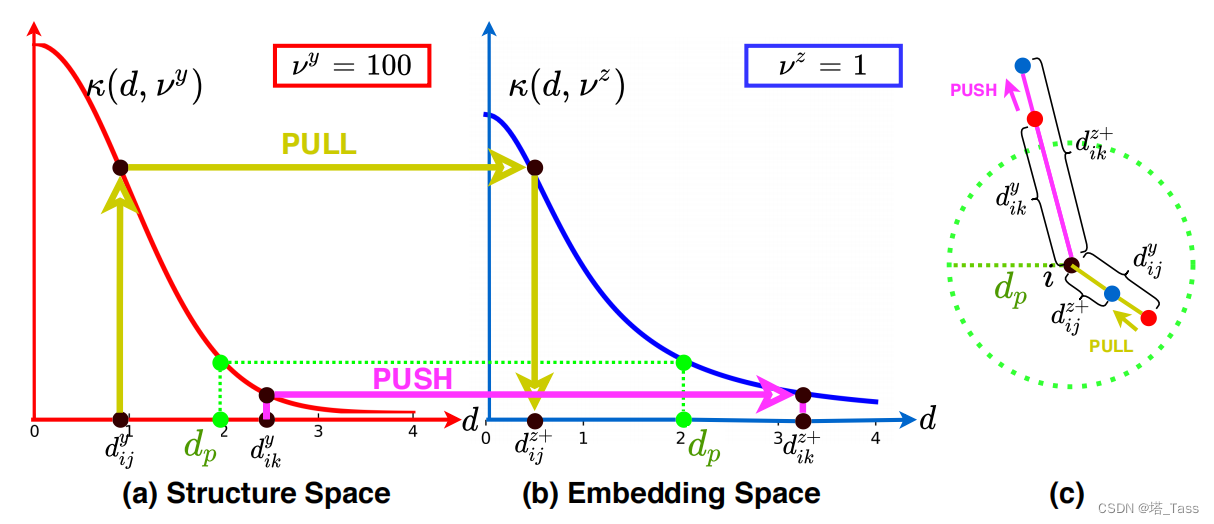
图4：推拉性质。如果$d^y<d_p$，那么$d^{z+}<d^y$(黄色线拉近d)，如果$d^y>d_p$，那么$d^{z+}>d^y$(粉色线拉远d)

引理1：推拉性质
当$v^y,v^z$时，令$d^{z+}={\kappa }^{-1}(\kappa (d,v^y),v^z)$为最优化损失函数的解，那么存在$d_p$使得$(d^y-d_p)(d^{z+}-d^y)>0$

DLME的伪代码：

先将原始和增广数据集随机采样，点对经过两个网络，计算在第一个网络下和第二个网络下embedding后的距离，再根据距离计算计算相似度，得到的结果用于损失函数的优化。

4. 实验

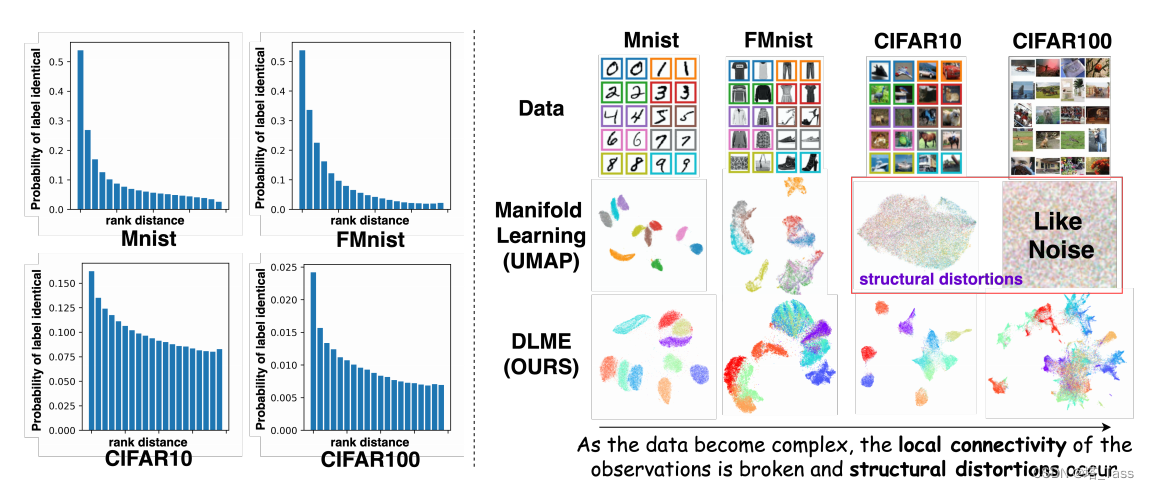
图5：（左）标签识别概率与排序距离的条形图。条形图的左端越高，表示最近邻样本的相同标签的概率越高，这意味着局部连通性得到了保证。（右）ML方法（UMAP）在四个图像数据集上的结果。复杂数据无法保证局部近邻连接导致失败。所提出的DLME方法在更复杂的CIFAR数据集上具有更好的嵌入结果。

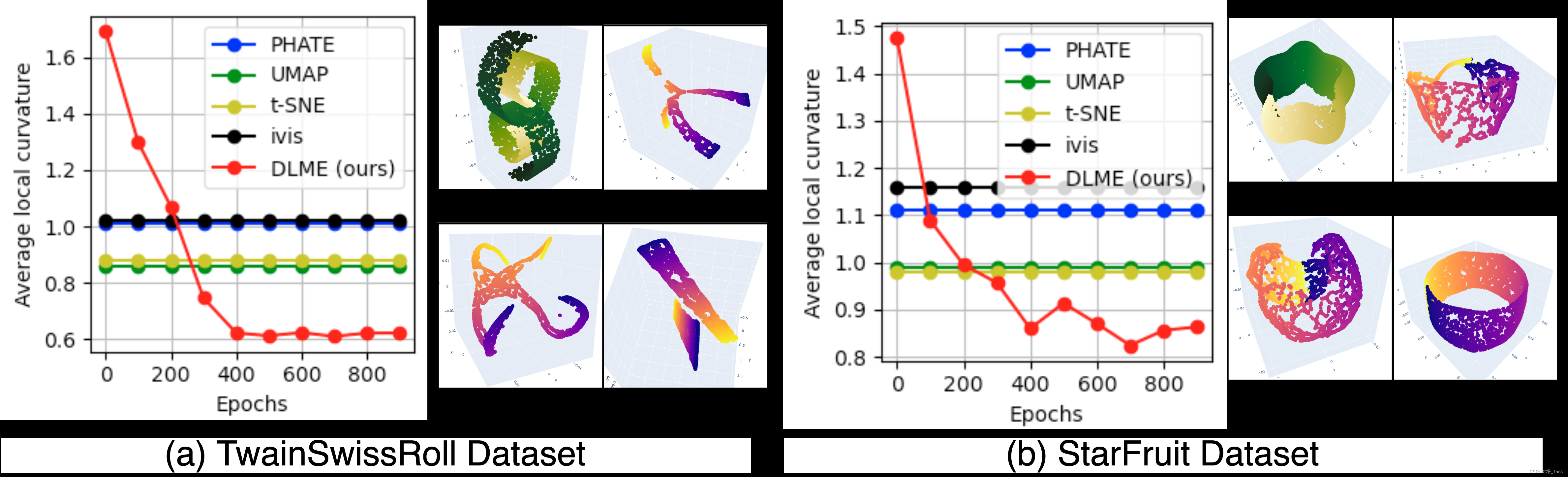
图6：SwissRoll和StarFruit数据集上不同方法得到的平均局部曲率和散点图。这两个例子表明，DLME可以通过优化局部曲率来尽可能地得到合理的平坦embedding。

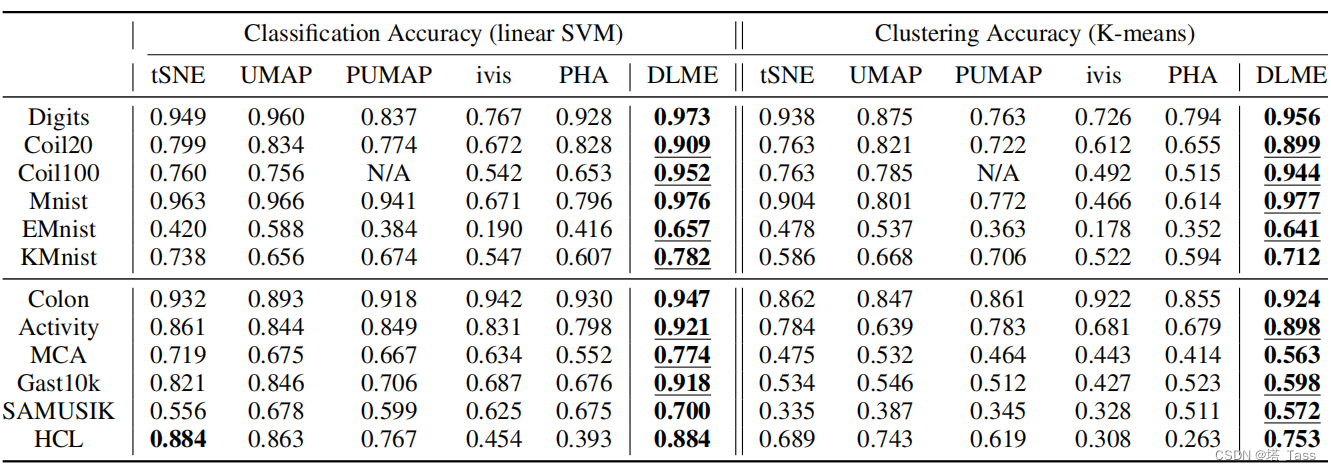
表1：在12个数据集上的效果，我们汇报了在下游线性分类和k-means聚类上的效果，下划线表示准确率高出最好的方法超过5%。

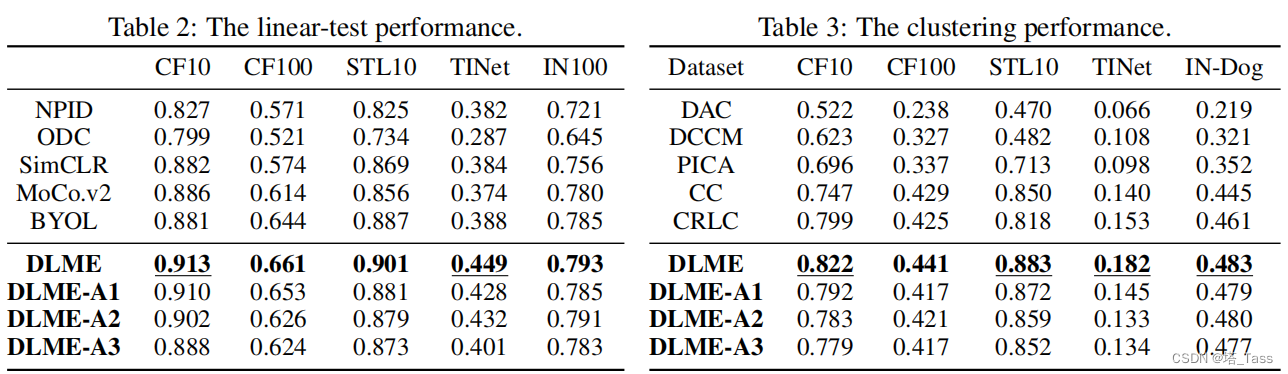
表2：我们也汇报了和对比学习方法的比较，许多对比学习方法得到的embedding产生了崩溃解以至于无法应用于下游的聚类任务。

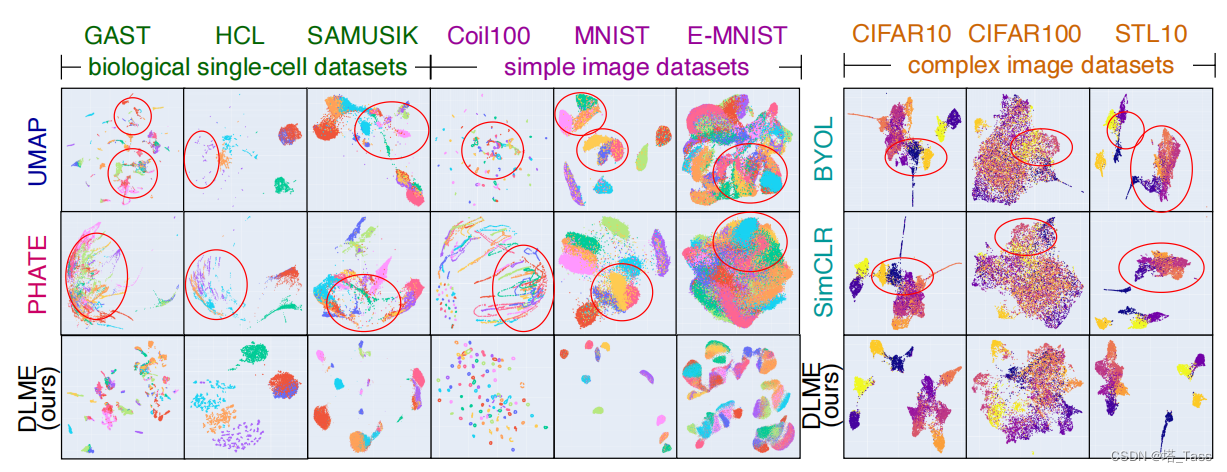
图7：生物数据集、简单图像数据集和复杂图像数据集的可视化结果。画圈的部分标出了baseline方法的聚类互相重叠