Java笔记_11常见算法
- 一、常见算法
- 1.1、查找算法
- 1.2、排序算法
- 二、Arrays
- 三、Lambda表达式
- 四、综合练习
- 4.1、按照要求进行排序
- 4.2、不死神兔
- 4.3、猴子吃桃子
- 4.4、爬楼梯
一、常见算法
1.1、查找算法
- 基本查找

package Common_algorithms.Basic_Search;
import java.util.ArrayList;
import java.util.Scanner;
public class Dome1 {
public static void main(String[] args) {
//练习1
int[] arr = {12,123,44,55,332,24,75,11};
System.out.println("请输入一个数,判断是否存在数组内部.存在即打印出来其下标,否则是-1");
Scanner sc= new Scanner(System.in);
String number = sc.nextLine();
int num = Integer.parseInt(number);
System.out.println(serach(arr, num));
}
public static int serach(int[] arr,int num){
for (int i = 0; i < arr.length; i++) {
if (num == arr[i]){
return i;
}
}
return -1;
}
}
package Common_algorithms.Basic_Search;
import java.util.ArrayList;
import java.util.Scanner;
public class Dome2 {
public static void main(String[] args) {
//练习2
int[] arr = {11,123,44,55,332,24,123,75,11};
System.out.println("请输入一个数,判断是否存在数组内部.存在即打印出来其下标");
Scanner sc= new Scanner(System.in);
String number = sc.nextLine();
int num = Integer.parseInt(number);
System.out.println(serach(arr, num));
}
private static Object serach(int[] arr, int num) {
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
if(num == arr[i]){
list.add(i);
}
}
return list;
}
}
- 二分查找/折半查找
- 前提条件:数组中的数据必须是有序的
- 核心逻辑:每次排除一半的查找范围
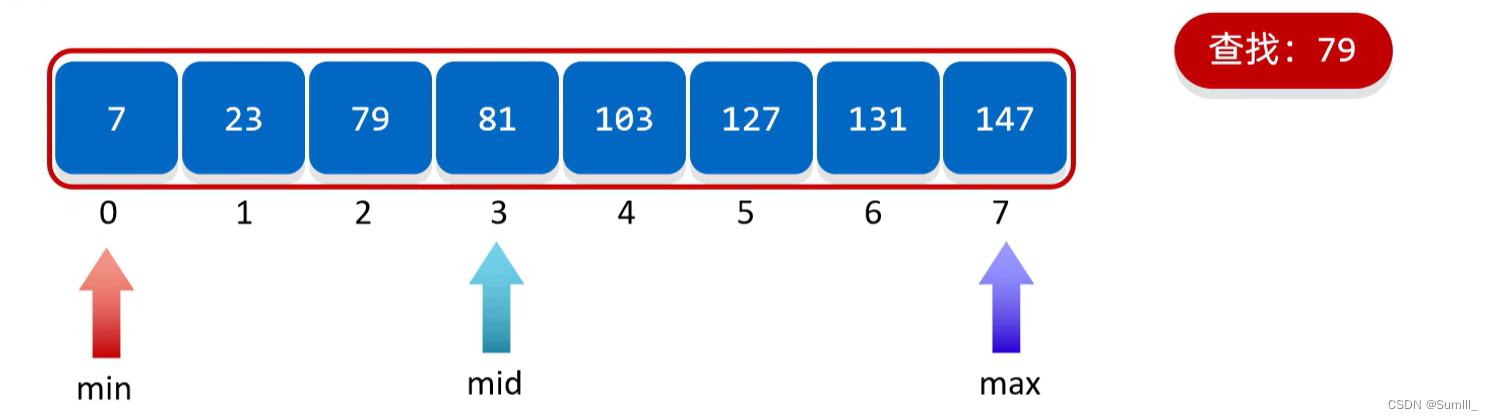
- min和max表示当前要查找的范围
- mid是在min和max中间的
- 如果要查找的元素在mid的左边,缩小范围时,min不变,max等于mid减1
- 如果要查找的元素在mid的右边,缩小范围时,max不变,min等于mid加1
package Common_algorithms.Basic_Search;
import java.util.Scanner;
public class Dome3 {
public static void main(String[] args) {
//二分查找
int[] arr = {1,2,3,4,5,6,7,8,11,23,44,54};
Scanner sc= new Scanner(System.in);
System.out.println("请输入你要查找的数据");
String s = sc.nextLine();
int num = Integer.parseInt(s);
System.out.println(search(arr, num));
}
public static int search (int[] arr ,int num){
int min = 0;
int max = arr.length-1;
while (true){
if(min>max){
return -1;
}
int mid = (min+max)/2;
if(arr[mid]>num){
//如果中间索引的值大于num则最大索引为mid索引的前面一个
max = mid - 1;
} else if (arr[mid]<num) {
//如果中间索引的值小于num则最小索引为mid索引的后面一个
min = mid+1;
}else {
return mid;
}
}
}
}
- 插值查找
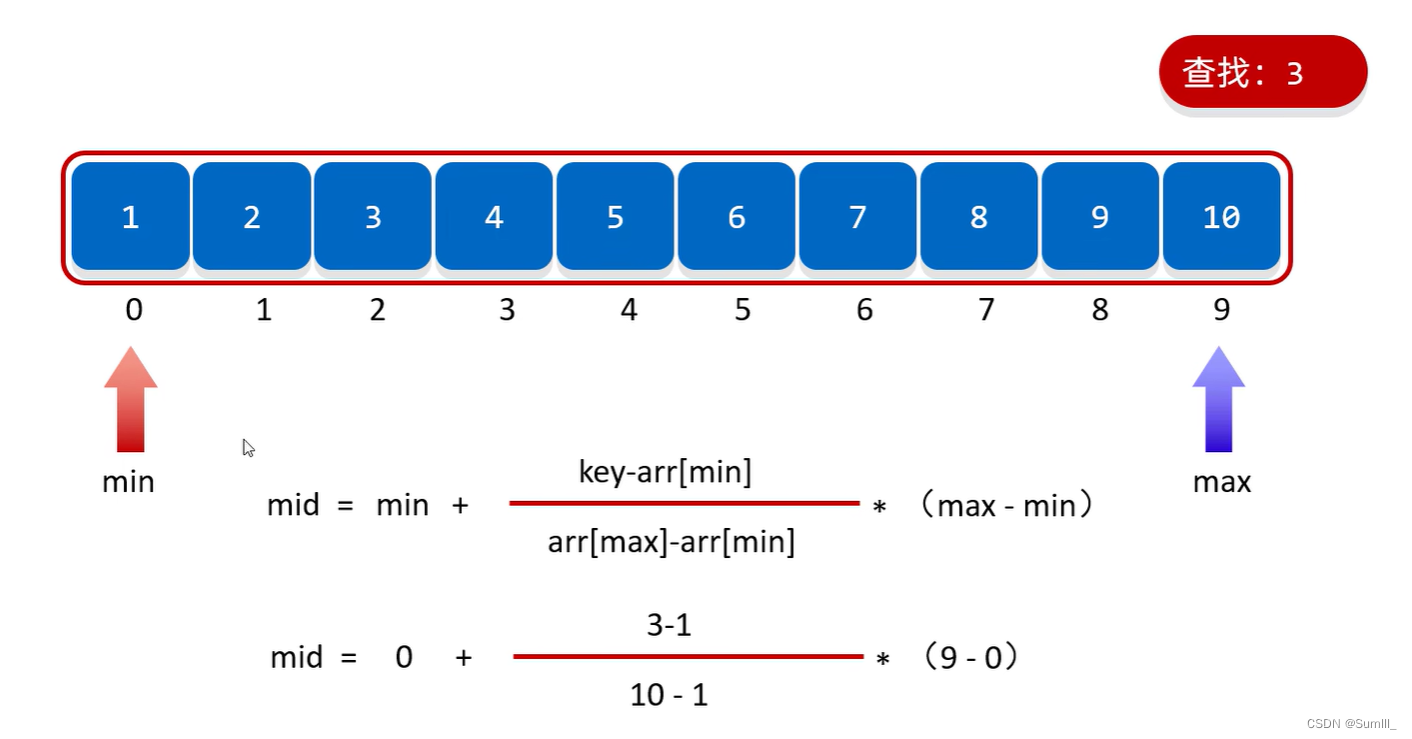
- 斐波那契查找

- 分块查找

- 分块的原则1:前一块中的最大数据,小于后一块中所有的数据(块内无序,块间有序)
- 分块的原则2:块数数量一般等于数字的个数开根号。比如:16个数字一般分为4块左右。
心 - 核心思路:先确定要查找的元素在哪一块,然后在块内挨个查找。
package Common_algorithms.Basic_Search;
public class BlockSearch {
public static void main(String[] args) {
int[] arr = {16,5,9,12,21,18,
32,23,37,26,45,34,
50,48,61,52,73,66};
//将数组中的子项分成块
block b1 = new block(21,0,5);
block b2 = new block(45,6,11);
block b3 = new block(73,12,17);
block[] arr1 = {b1,b2,b3};
int number = 16;
int getindex = getindex(arr1, number, arr);
System.out.println(getindex);
}
public static int getindex(block[] arr1,int number,int[] arr ){
//先将该数字在某个块内的位置确定下来
int getindex = findindexblock(arr1, number);
//获得该块的起始索引和结束索引
int startindedx = arr1[getindex].getStartindex();
int endindex = arr1[getindex].getEndindex();
//遍历的到该数字在数组中的位置
for (int i = startindedx; i <=endindex ; i++) {
if(arr[i] == number){
return i;
}
}
return -1;
}
public static int findindexblock (block[] arr,int num){
for (int i = 0; i < arr.length; i++) {
//如果小于这个块的最大值,说明num就在这个块中
if(num<=arr[i].getMax()){
return i;
}
}
return -1;
}
//创建一个block类,分装数组的数据
static class block{
private int max ;
private int startindex ;
private int endindex ;
public block() {
}
public block(int max, int startindex, int endindex) {
this.max = max;
this.startindex = startindex;
this.endindex = endindex;
}
public int getMax() {
return max;
}
public void setMax(int max) {
this.max = max;
}
public int getStartindex() {
return startindex;
}
public void setStartindex(int startindex) {
this.startindex = startindex;
}
public int getEndindex() {
return endindex;
}
public void setEndindex(int endindex) {
this.endindex = endindex;
}
public String toString() {
return "block{max = " + max + ", startindex = " + startindex + ", endindex = " + endindex + "}";
}
}
}
1.2、排序算法
- 冒泡排序
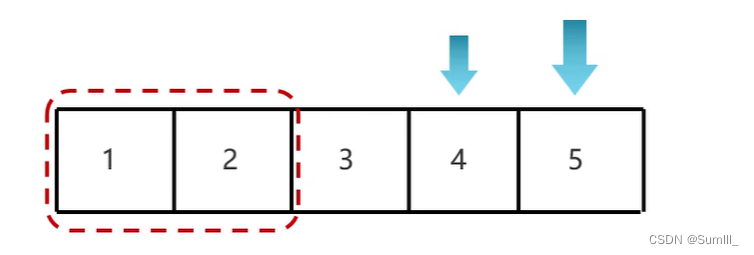
- 相邻的元素两两比较,大的放右边,小的放左边。
- 第一轮比较完毕之后,最大值就已经确定,第二轮可以少循环一次,后面以此类推。
- 如果数组中有n个数据,总共我们只要执行n-1轮的代码就可以。
package Common_algorithms.sort;
public class Dome1 {
public static void main(String[] args) {
int[] arr = {1,3,2,5,6,7,8,5,3,12,1,3,4,5,6};
for (int i = 0; i < arr.length-1; i++) {
for (int i1 = 0; i1 < arr.length-1; i1++) {
if(arr[i1]>arr[i1+1]){
int temp = arr[i1];
arr[i1] = arr[i1+1];
arr[i1+1] = temp;
}
}
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
}
- 选择排序
- 从O索引开始,拿着每一个索引上的元素跟后面的元素依次比较,小的放前面,大的放后面,以此类推。
package Common_algorithms.sort;
public class Dome1 {
public static void main(String[] args) {
int[] arr = {1,3,2,5,6,7,8,5,3,12,1,3,4,5,6};
for (int i = 0; i < arr.length-1; i++) {
for (int i1 = i + 1; i1 < arr.length-1; i1++) {
if(arr[i]>arr[i1]){
int temp = arr[i];
arr[i] = arr[i1];
arr[i1] = temp;
}
}
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
}
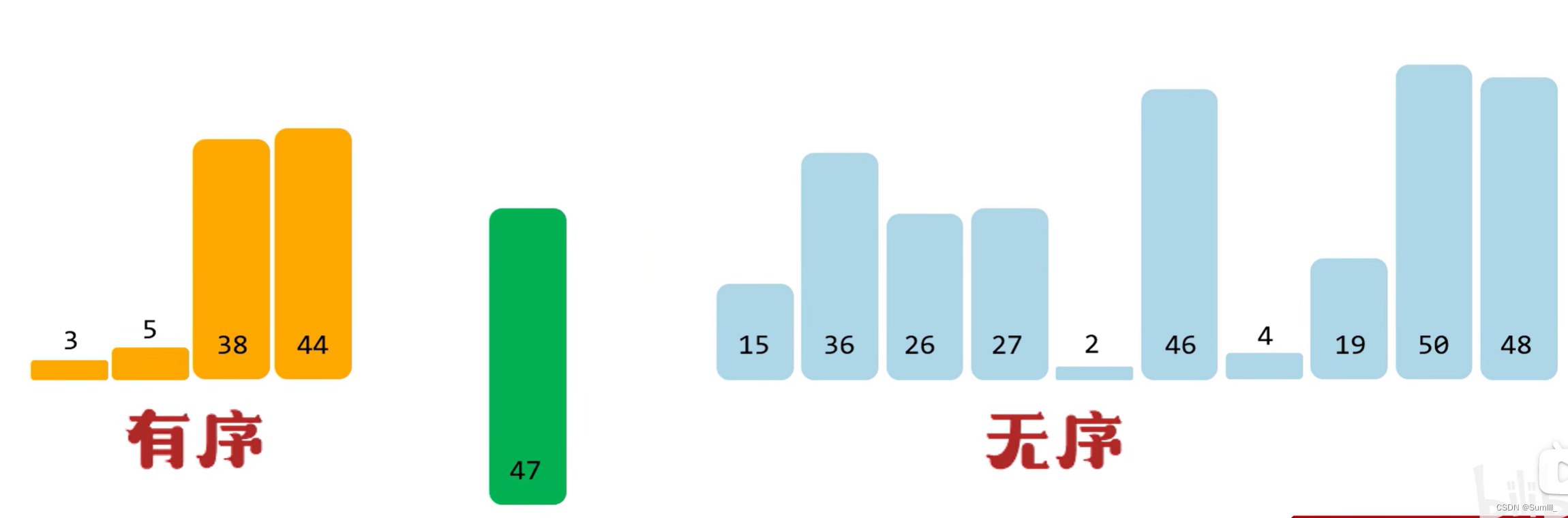
- 插入排序
插入排序∶将0索引的元素到N索引的元素看做是有序的,把N+1索引的元素到最后一个当成是无序的。遍历无序的数据,将遍历到的元素插入有序序列中适当的位置,如遇到相同数据,插在后面。
N的范围:0~最大索引
package Common_algorithms.sort;
public class Dome2 {
public static void main(String[] args) {
int[] arr = {1,2,3,4,122,3,4,44,123,22,33,14,6,45,64,34,22,11};
//得到无序数组的那一组是从那个索引开始的
int startindex = -1;
for (int i = 0; i < arr.length; i++) {
if(arr[i]>arr[i+1]){
System.out.println("这个数组分块的索引"+i);
startindex = i+1;
break;
}
}
//遍历从startindex开始到最后一个元素,依次得到无序的那一组数据中的每一个元素
for (int i = startindex; i < arr.length; i++) {
//记录当前要插入的数据的索引
int j = i;
while (arr[j]<arr[j-1]&&j>0){
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
j--;
}
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
- 递归算法
- 递归指的是方法中调用方法本身的现象
- 递归的注意点:递归一定要有出口,否则就会出现内存溢出
递归算法的作用:
- 把一个复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。
- 递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算
书写递归的两个核心:
- 找出口:什么时候不再调用方法。
- 找规则:如何把大问题变成规模较小的问题
package Common_algorithms.sort;
public class Dome3 {
public static void main(String[] args) {
System.out.println(getsum(1000));
}
public static int getsum (int num){
if(num == 1){
return 1;
}
//大问题拆成小问题
//1~100之间的和 = 100 + (1~99之间的和)
//1~99之间的和 = 99 + (1~98之间的和)
//。。。
//1~2之间的和 = 2 + (1~1之间的和)
//1~1之间的和 = 1(递归的出口)
//方法内部再次调用方法的时候,参数必须要更加接近出口
return num + getsum(num-1);
}
}
- 快速排序
第一轮: 把0索引的数字作为基准数,确定基准数在数组中正确的位置。比基准数小的全部在左边,比基准数大的全部在右边。
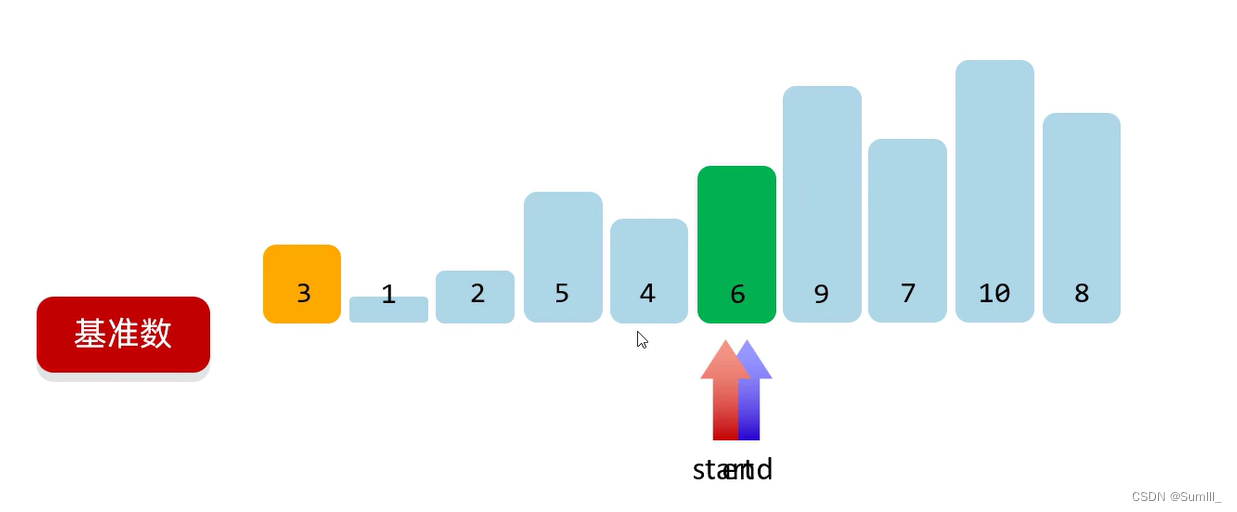
package Common_algorithms.sort;
public class Dome4 {
public static void main(String[] args) {
int[] arr = {8,23,4,5,6,22,11,44,34,6,5,4};
qruaksort(arr,0,arr.length-1);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}
//将基准数调到数组的基准位置
private static void qruaksort(int[] arr,int i,int j) {
int start = i;
int end = j;
if (start>end){
return;
}
//记录基准数
int baseNumber = arr[i];
while (end != start){
//end从后面往前找
while (true){
if(end<=start||arr[end]<baseNumber){
break;
}
end--;
}
//start从前面往后找
while (true){
if(end<=start||arr[start]>baseNumber){
break;
}
start++;
}
//把end和start指向的元素进行交换
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
//当start和end指向了同一个元素的时候,那么上面的循环就会结束
//表示已经找到了基数在数组中应存的位置
//基准数归位
int temp = arr[i];
arr[i] = arr[start];
arr[start] = temp;
//确定i左边的范围,并且重复该函数
qruaksort(arr,0,start-1);
//确定i右边的范围,并且重复该函数
qruaksort(arr,start+1,j);
}
}
二、Arrays
操作数组的工具类
| 方法名 | 说明 |
|---|---|
| public static String toString(数组) | 把数组拼接成一个字符串 |
| public static int binarySearch(数组,查找的元素) | 二分查找法查找元素 |
| public static int[] copyOf(原数组,新数组长度) | 拷贝数组 |
| public static int[] copyOfRange(原数组,起始索引,结束索引) | 拷贝数组(指定范围) |
| public static void fill(数组,元素) | 填充数组 |
| public static void sort(数组) | 按照默认方式进行数组排序 |
| public static void sort(数组,排序规则) | 按照指定的规则排序 |
-
binarySearch:二分查找法查找元素
- 细节1:二分查找的前提:数组中的元素必须是有序,数组中的元素必须是升序的
- 细节2:如果要查找的元素是存在的,那么返回的是真实的索引
但是,如果要查找的元素是不存在的,返回的是 -插入点– 1
-
copyof:拷贝数组
- 参数一:老数组
- 参数二:新数组的长度
- 方法的底层会根据第二个参数来创建新的数组
- 如果新数组的长度是小于老数组的长度,会部分拷贝
- 如果新数组的长度是等于老数组的长度,会完全拷贝
- 如果新数组的长度是大于老数组的长度,会补上默认初始值
-
copyOfRange:拷贝数组
- 包头不包尾,包左不包右
-
sort排序数组
package Common_algorithms.sort;
import java.util.Arrays;
import java.util.Comparator;
public class Dome5_Arrays_sort {
public static void main(String[] args) {
Integer[] arr = {1,2,3,4,5,6,7,8,8,9};
//第二个参数是一个接口,所以我们在调用方法的时候,需要传递这个接口的实现类对象,作为排序的规则。
//但是这个实现类,我只要使用一次,所以就没有必要单独的去写一个类,直接采取匿名内部类的方式就可以了
//底层原理:
//利用插入排序 + 二分查找的方式进行排序的。
//默认把О索引的数据当做是有序的序列,1索引到最后认为是无序的序列。
// 遍历无序的序列得到里面的每一个元素,假设当前遍历得到的元素是A元素
//把A往有序序列中进行插入,在插入的时候,是利用二分查找确定A元素的插入点。
//拿着A元素,跟插入点的元素进行比较,比较的规则就是compare方法的方法体
//如果方法的返回值是负数,拿着A继续跟前面的数据进行比较
//如果方法的返回值是正数,拿着A继续跟后面的数据进行比较
//如果方法的返回值是0,也拿着A跟后面的数据进行比较
//直到能确定A的最终位置为止。
//compare方法的形式参数:
//参数一o1:表示在无序序列中,遍历得到的每一个元素
// 参数二 o2:有序序列中的元素
//返回值:
//负数:表示当前要插入的元素是小的,放在前面正数:表示当前要插入的元素是大的,放在后面
//0:表示当前要插入的元素跟现在的元素比是一样的们也会放在后面
//简单理解
// o1 - o2:升序排列
// o2 - o1:降序排列
Arrays.sort(arr, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
System.out.println(Arrays.toString(arr));
}
}
三、Lambda表达式
-
函数式编程
函数式编程(Functional programming)是一种思想特点。
函数式编程思想,忽略面向对象的复杂语法,强调做什么,而不是谁去做。 -
Lambda表达式的标准格式
Lambda表达式是JDK8开始后的一种新语法形式。 -
注意点:
- Lambda表达式可以用来简化匿名内部类的书写
- Lambda表达式只能简化函数式接口的匿名内部类的写法
- 接口中只能有一个抽象方法
- 函数式接口:
有且仅有一个抽象方法的接口叫做函数式接口,接口上方可以加@FunctionalInterface注解
-
Lambda的好处?
Lambda是一个匿名函数,我们可以把Lambda表达式理解为是一段可以传递的代码,它可以写出更简洁、更灵活的代码,作为一种更紧凑的代码风格,使Java语言表达能力得到了提升。
package Common_algorithms.LambdaDome;
import java.sql.SQLOutput;
public class Dome1 {
public static void main(String[] args) {
/*m(new swim() {
@Override
public void swimming(){
System.out.println("正在游泳");
}
});
}*/
m(()->{
System.out.println("正在游泳");
}
);
}
public static void m (swim s){
s.swimming();
}
@FunctionalInterface
interface swim{
public abstract void swimming();
}
}
- Lambda表达式的省略写法
- 省略核心:可推导,可省略
package Common_algorithms.LambdaDome;
import java.util.Arrays;
import java.util.Comparator;
public class Dome2 {
public static void main(String[] args) {
Integer[] arr = {1,4,2,3,4,5,7,9,8};
Arrays.sort(arr, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
});
Arrays.sort(arr, (o1, o2)-> o2-o1);
System.out.println(Arrays.toString(arr));
}
}
- 参数类型可以省略不写。
- 如果只有一个参数,参数类型可以省略,同时()也可以省略。
- 如果Lambda表达式的方法体只有一行,大括号,分号,
return可以省略不写,需要同时省略。

package Common_algorithms.LambdaDome;
import java.util.Arrays;
import java.util.Comparator;
public class Text1 {
public static void main(String[] args) {
String[] arr = {"aas","aa","a","asaaaa","aaaaa"};
Arrays.sort(arr, new Comparator<String>() {
@Override
public int compare(String o1, String o2) {
return o1.length()-o2.length();
}
});
Arrays.sort(arr, (o1, o2)->o2.length()-o1.length());
System.out.println(Arrays.toString(arr));
}
}
四、综合练习
4.1、按照要求进行排序

package Common_algorithms.Test.Test1;
import javax.net.ssl.CertPathTrustManagerParameters;
import java.util.Arrays;
import java.util.Comparator;
public class TestDome {
public static void main(String[] args) {
Grilfrident g1 = new Grilfrident("xiaoqiu",17,173);
Grilfrident g2 = new Grilfrident("xiaoli",18,165);
Grilfrident g3 = new Grilfrident("xiaobi",18,165);
Grilfrident[] arr = {g1,g2,g3};
Arrays.sort(arr, (o1, o2)->{
int temp = o1.getAge()-o2.getAge();
temp = temp == 0?o1.getHeight()-o2.getHeight():temp;
temp = temp == 0?o1.getName().compareTo(o2.getName()):temp;
if(temp>0){
return 1;
}else if(temp<0){
return -1;
}else {
return 0;
}
}
);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i].toString());
}
}
}
4.2、不死神兔

package Common_algorithms.Test.Test2;
public class TestDome {
public static void main(String[] args) {
int[] fn = new int[12];
fn[0] = 1;
fn[1] = 1;
for (int i = 2; i < fn.length; i++) {
fn[i] = fn[i-1]+fn[i-2];
}
System.out.println(fn[11]);
}
}
package Common_algorithms.Test.Test2;
public class TestDome2 {
public static void main(String[] args) {
int num = 12;
System.out.println(getNum(12));
}
//使用递归的方法来完成
public static int getNum (int num){
//判断当num为1或2时所得到的值
//为递归的出口
if(num == 1||num==2){
return 1;
} else {
return getNum(num-1) + getNum (num-2);
}
}
}
4.3、猴子吃桃子

package Common_algorithms.Test;
public class Test3 {
public static void main(String[] args) {
/*
* 有一堆桃子,猴子第一天吃了其中的一半,并多吃了一个!以后每天猴子都吃当前剩下来的一半,然后再多吃一个,
第10天的时候(还没吃),发现只剩下一个桃子了,请问,最初总共多少个桃子?
day10: 1
day9: (day10 + 1)* 2= 4
day8: (day9 + 1)* 2= 10
1.出口
day== 10剩下1
2.规律
每一天的桃子数量都是后一天数量加1,乘以2
* */
System.out.println(getNum(1));
}
public static int getNum(int day){
if(day<=0||day>=11){
return -1;
}
if(day ==10){
return 1;
}
return (getNum(day+1)+1)*2;
}
}
4.4、爬楼梯

package Common_algorithms.Test;
public class Test4 {
public static void main(String[] args) {
System.out.println(getCount(20));
}
public static int getCount(int n){
if(n==1){
return 1;
} else if (n==2) {
return 2;
}
//20台阶的爬法相当于 19台阶爬法 + 18台阶爬法
return getCount(n-1)+getCount(n-2);
}
}