传送门

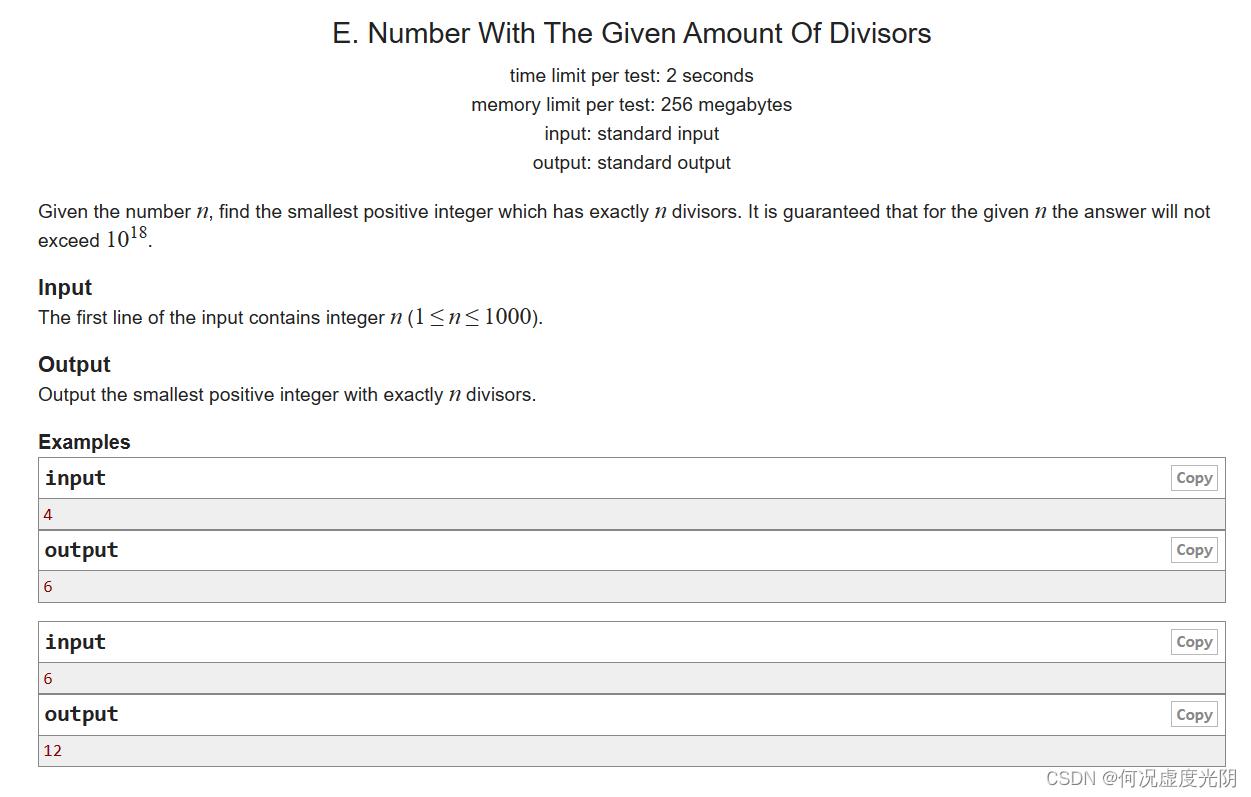
题意：求出整好有n个因子的最小整数。

思路：

 要找到恰好有n个因子的最小整数，我们可以利用质因数分解的思想来求解。设该整数的质因数分解式为：其中p1,p2,...,pn均为不同的质数，a1,a2,...,an均为正整数。则该整数一共有(a1+1)(a2+1)...(an+1)个因子。

因此，如果要使得该整数恰好有n个因子，那么必须满足上述各个指数ai都应当是0或1，且所有指数之积等于n。并且我们还应当尽量让各个指数相等，以保证这个整数最小。

举个例子，如果n=4，则我们需要找到一个形如的整数，因为它有4个因子：1，p1，p2，和p1*p2。而如果我们选择p1=2，p2=3，则所求的最小整数为= 24。

可以用dfs方法去找。

AC代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int a[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
int ans=1e18;
void dfs(int n,int i,int l,int x){
	if(n==1){
		ans=min(ans,x);
		return ;
	}
	for(int j=2;j<=n&&j<=l;j++){
		if(x>1e18/a[i]){
			break;
		}
		x*=a[i];
		if(n%j==0){
			dfs(n/j,i+1,j,x);
		}
	}
}
signed main(){
	int n;
	cin>>n;
	dfs(n,0,1e9,1);
	cout<<ans<<'\n';
}