提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- PSO算法原理
- 进化操作
- 算法流程图
- matlab代码实现
- main函数部分
- 适应度函数部分
- PSO算法主体
- 测试结果 (F1~F6)
PSO算法原理
粒子群优化( Particle Swarm Optimization,PSO) 算法是 Kennedy 和 Eberhart〔1〕在 1995 年首次提出一种 模拟鸟群和鱼群等动物寻找食物的社会行为的群智能优化算法。
在粒子群算法中,每个粒子拥有两个特征:速度和位置,如下:

进化操作
粒子的位置变化公式:

其中:
c1 和 c2是学习因子,本文定义c1=1.6,c2=1.8
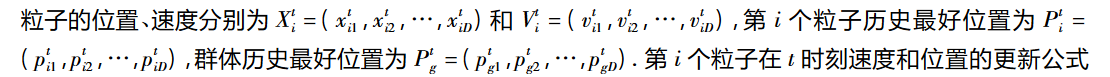
第一个公式是速度更新的公式:
该公式的第一项是惯性部分、第二项是认知部分、第三项是社会部分。
认知部分即:向着自身在历史中所处的最好位置的方向移动。
社会部分即:向着群体中最好的位置的方向移动。
为了改善PSO的性能,Shi和Eberhart引入了惯性权重omiga。速度更新公式即为:
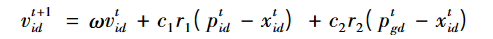
引入omiga的目的是为了较好地平衡PSO算法的全局搜索能力和局部搜索能力,这样的PSO算法也被称为标准PSO算法。
本文定义omiga的取值范围为
①:权重向量线性递减,Shi和Eberhart将omiga的取值范围定义为[0.4,0.9]
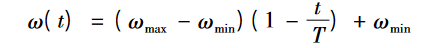
②:也有些研究将权重向量线性递增,公式如下,本文验证部分测试集的时候效果不如权重向量线性递减策略。
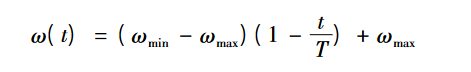
算法流程图
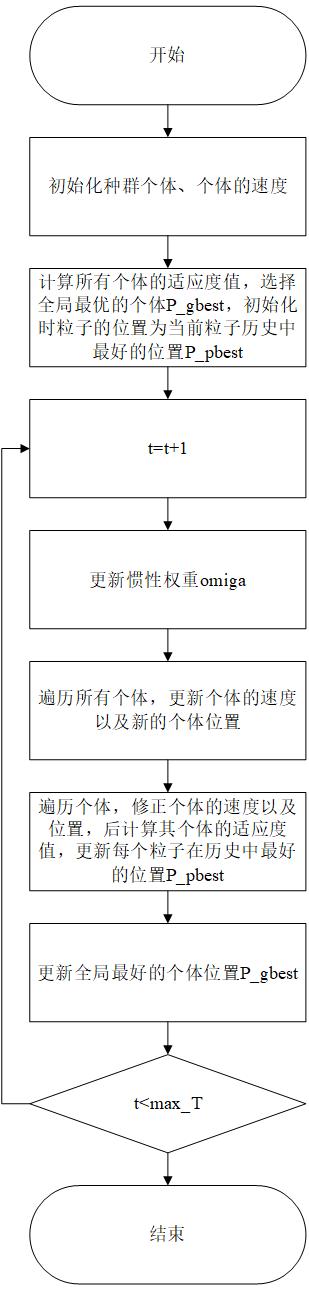
matlab代码实现
main函数部分
clear all;
close all;
clc;
N=300;
Dim=30;
ub=100;
lb=-100;
T=500;
% 学习因子
c1=1.6;
c2=1.8;
% 速度系数
vel=0.01;
[P_gbest,G_best]=PSO(Dim,ub,lb,vel,N,T,c1,c2);
figure,
plot(G_best,'Color','red');
xlim([1,500]);
适应度函数部分
function my_fitness=my_function(X)
%F1测试问题[-100,100] min=0
% o=sum(X.^2);
% my_fitness=o;
%F2测试问题[-10,10] min=0;
% o=sum(abs(X))+prod(abs(X));
% my_fitness=o;
%F3测试问题——结果极差 min=0
% dim=size(X,2);
% o=0;
% for i=1:dim
% o=o+sum(X(1:i))^2;
% end
% my_fitness=o;
%F4测试问题——结果极差[-100,100] min=0
% o=max(abs(X));
% my_fitness=o;
%F5测试问题[-30,30] min=0
% dim=size(X,2);
% my_fitness=sum(100*(X(2:dim)-(X(1:dim-1).^2)).^2+(X(1:dim-1)-1).^2);
%F6测试问题[-100,100] min=0
o=sum(abs((X+.5)).^2);
my_fitness=o;
end
PSO算法主体
function [P_gbest,G_best]=PSO(Dim,ub,lb,vel,N,T,c1,c2)
%% 初始化种群
Pop=zeros(N,Dim);
Pop_vel=zeros(N,Dim);
for i=1:N
for j=1:Dim
Pop(i,j)=lb+rand().*(ub-lb);%初始化个体
Pop_vel(i,j)=vel*(lb+rand().*(ub-lb));%初始化个体速度
end
end
% 计算个体的适应度值
for i=1:N
fitness(i)=my_function(Pop(i,:));
end
[fit_gbest,fit_gbest_index]=min(fitness);
P_gbest=Pop(fit_gbest_index,:);%全局中最好的个体
% 初始时 每个个体当前位置即历史中最好的位置
P_pbest=Pop;
%% 进化部分
for t=1:T
%omiga=2-(2-0.4)*(t/T);%定义范围为[0.4,2],随着迭代次数线性减少
omiga=(0.9-0.4)*(1-(t/T))+0.4;%惯性权重线性递减策略
%omiga=(0.4-0.9)*(1-(t/T))+0.9;%惯性权重递增策略——效果不佳
% 遍历所有个体,更新所有个体的位置
for i=1:N
for j=1:Dim
r1=rand();
r2=rand();
Pop_vel(i,j)=omiga*Pop_vel(i,j)+c1*r1*(P_pbest(i,j)-Pop(i,j))+c2*r2*(P_gbest(j)-Pop(i,j));
Pop(i,j)=Pop(i,j)+Pop_vel(i,j);
end
end
% 遍历个体计算适应度值
for i=1:N
Flag4Up=Pop(i,:)>ub;
Flag4Lp=Pop(i,:)<lb;
Pop(i,:)=(Pop(i,:).*(~(Flag4Up+Flag4Lp)))+Flag4Up.*ub+Flag4Lp.*lb;%修正粒子群的位置
FlagUp=Pop_vel(i,:)>vel*ub;
FlagLp=Pop_vel(i,:)<vel*lb;
Pop_vel(i,:)=(Pop_vel(i,:).*(~(FlagUp+FlagLp)))+FlagUp.*vel.*ub+FlagLp.*lb.*vel;%修正粒子群的速度
y=my_function(Pop(i,:));
if y<fitness(i)
P_pbest(i,:)=Pop(i,:);%更新在历史中每个粒子最好的位置
fitness(i)=y;
end
end
% 更新最好个体的位置
[fit_best,fit_best_index]=min(fitness);
G_best(t)=fit_best;
P_gbest=Pop(fit_best_index,:);
end
end
测试结果 (F1~F6)
F1
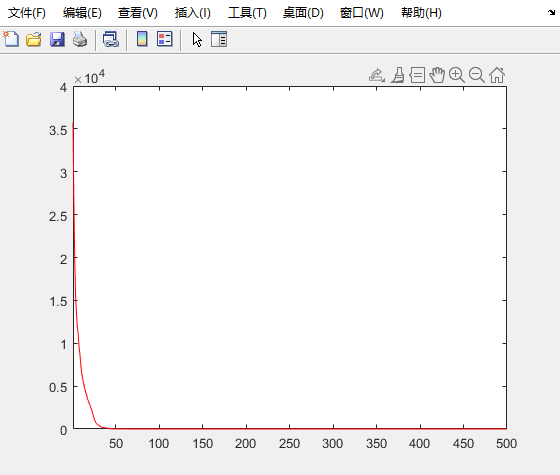
F2
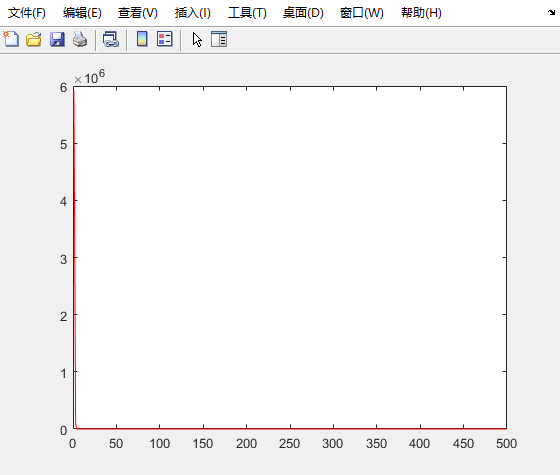
F3
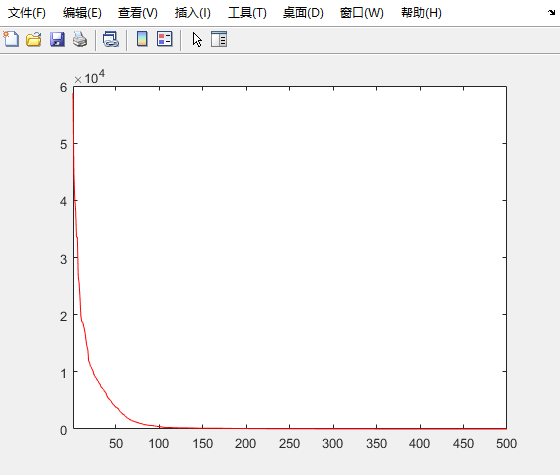
F4
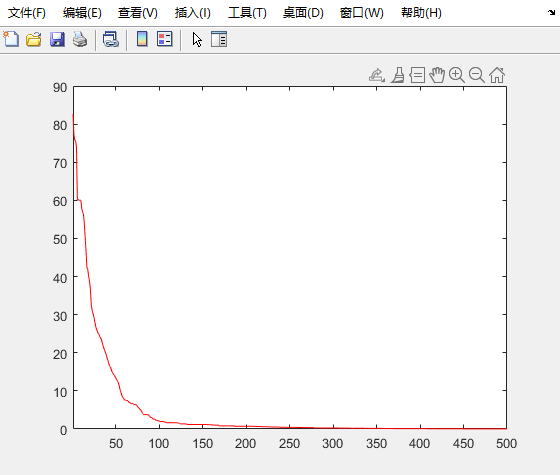
F5
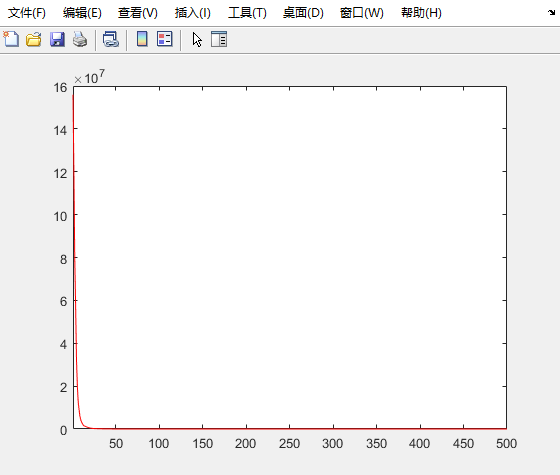
F6
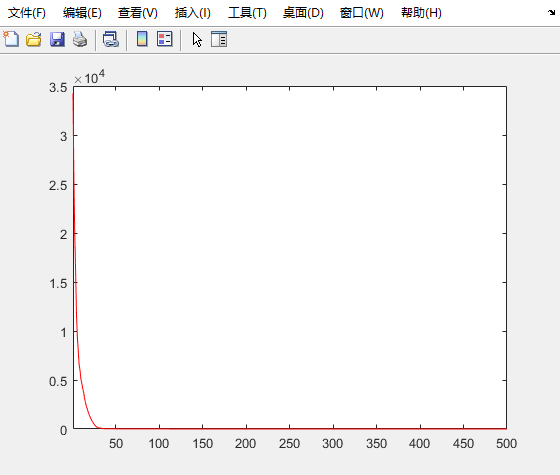





![[Golang] 设计模式以及单例设计模式实例实现](https://img-blog.csdnimg.cn/290cb82ff7834878aff2daa6c4a0bf4f.gif#pic_center)