说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

day37 十字链表

1.思路整理

1.1十字链表的数据结构：

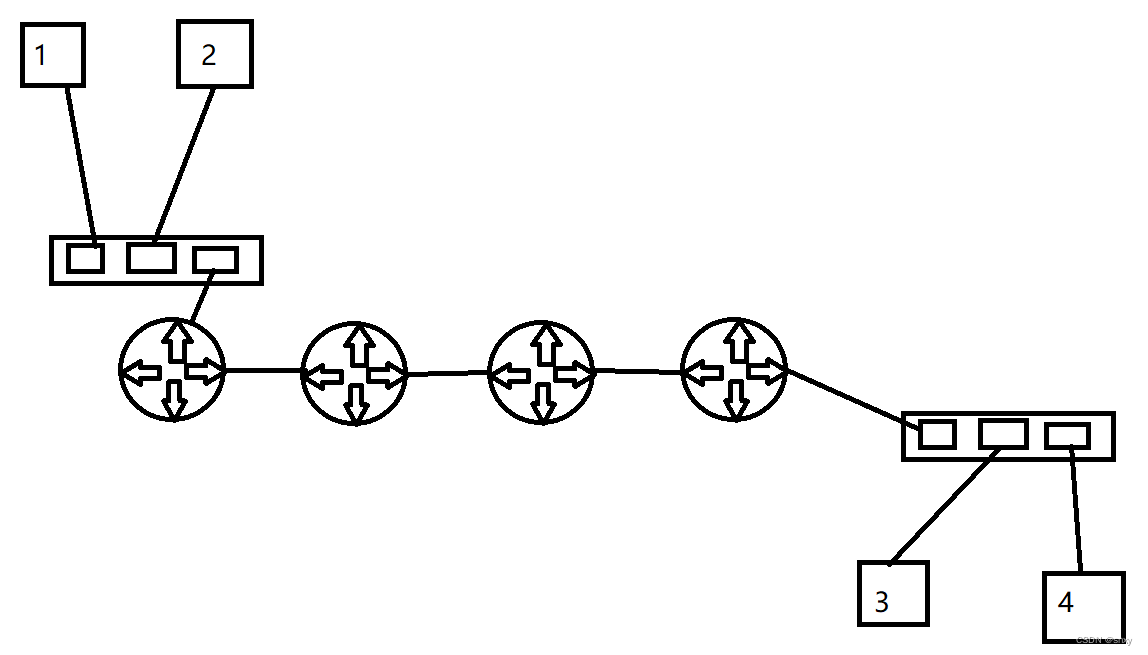
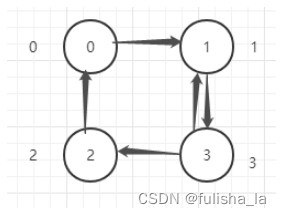
由弧节点和顶点节点组成。其中每个节点的含义一定要清楚，不然很容易就晕了（如下图）
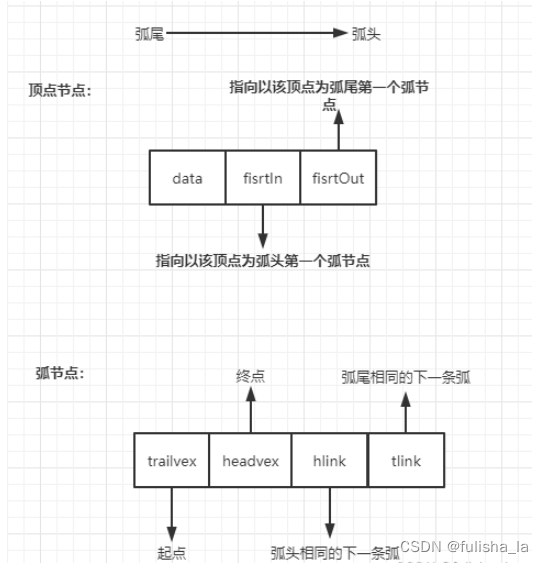
在这里插入图片描述

1.2 手动模拟十字链表

在知道了数据结构后手动模拟画出十字链表（十字链表我觉得画都很麻烦，所以一定要先弄懂他是怎么画的再去理解代码可能会更好些）其中起点和弧尾是相同表达意思，终点和弧头是相同表达意思
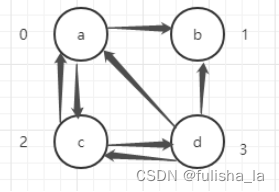
在这里插入图片描述

先画出度
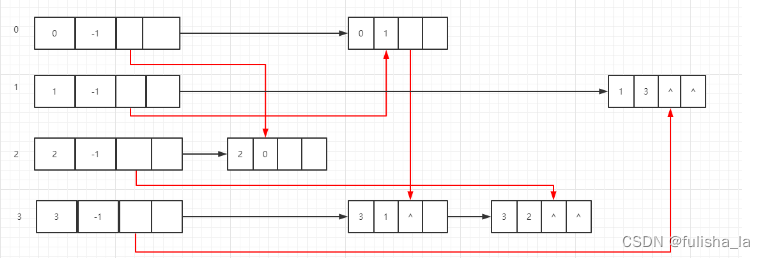
先将每个顶点的firstOut指向以该顶点为弧尾的第一个节点（如a节点，以a节点为弧尾的有b和c，其中a节点的fisrtOut指向以a为起点b为终点的弧节点），而在指向弧节点的4个域中，第4个域tlink,指的是链接弧尾相同的顶点（以a为弧尾b为弧头的弧节点的第4个域指向以a为弧尾c为弧头的弧节点），所以就有如下图：
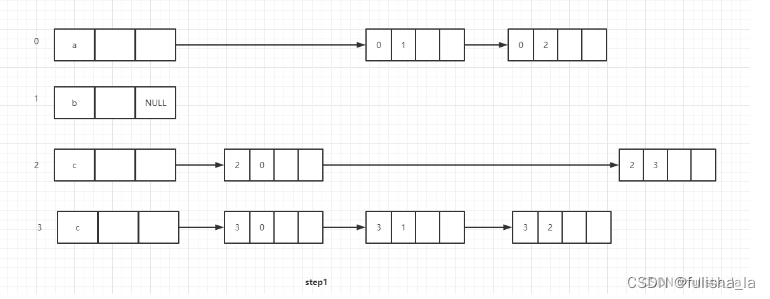
再画入度
上面只画出了弧尾的指向，现在画弧头的指向，画法和上面画弧尾指向类似。每个顶点的firstIn指向以该顶点为弧头的第一个节点（如a节点，以a节点为弧头的有c,d, 其中a节点的firstOut指向以c为起点a为终点的弧节点）而在指向弧节点的4个域中，第3个域hlink,指的是链接弧头相同的顶点（以c为弧尾a为弧头的弧节点的第3个域指向以d为弧尾a为弧头的弧节点）

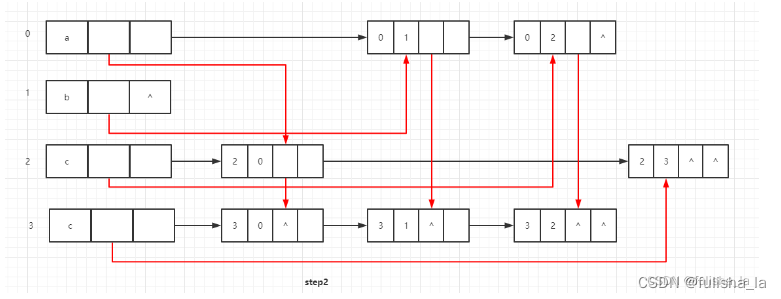
2.代码分析

2.1 十字链表的构造

我觉得十字链表的初始化比之前邻接矩阵和邻接表的初始化都更难，相比领接表容易找到出度，逆邻接表容易找到入度。十字链表即能很容易找到入度也很容易找到出度，所以他的数据结构也复杂一些。结合上面的图，可以将十字链表的初始化分为两部分，先初始化他的出度的链接，再初始化他入度的链接。

对于初始化出度的链接，判断出度是否为0，可以借助矩阵paraMatrix[i][j] == 0，i行j列表示i是否指向j（即是否以i顶点为弧尾）
对于初始化入度的链接,是遍历每一个头节点所链接的弧节点，使每个弧节点的第三个域（nextIn）去链接弧头相同的节点，弧节点的第二个域（即代码中的column）代表的是头节点的位置
tempColumnNodes[tempNode.column].nextIn = tempNode; // 说明他俩的弧头结点相同，
tempColumnNodes[tempNode.column] = tempNode; // 并更新结点的值
tempNode = tempNode.nextOut;// 判断下一个链接的结点

链接一个节点后要及时移动位置。感觉这段代码用语言不好描述，一定要图上模拟才更容易理解

package graph;

/**
 * @author： fulisha
 * @description：Orthogonal List for directed graph.
 */
public class OrthogonalList {
    class OrthogonalNode {
        int row;
        int column;
        /**
         * The next out node.
         */
        OrthogonalNode nextOut;

        /**
         * The next in node.
         */
        OrthogonalNode nextIn;

        /**
         * the first constructor
         * @param paraRow
         * @param paraColumn
         */
        public OrthogonalNode(int paraRow, int paraColumn) {
            row = paraRow;
            column = paraColumn;
            nextOut = null;
            nextIn = null;
        }
    }

    /**
     * The number of nodes. This member variable may be redundant since it is always  equal to headers.length
     */
    int numNodes;

    /**
     * The headers for each row.
     */
    OrthogonalNode[] headers;

    public OrthogonalList(int[][] paraMatrix) {
        numNodes = paraMatrix.length;

        // Step 1. Initialize. The data in the headers are not meaningful.
        OrthogonalNode tempPreviousNode, tempNode;
        headers = new OrthogonalNode[numNodes];

        // Step 2. Link to its out nodes.
        for (int i = 0; i < numNodes; i++) {
            headers[i] = new OrthogonalNode(i, -1);
            tempPreviousNode = headers[i];
            for (int j = 0; j < numNodes; j++) {
                if (paraMatrix[i][j] == 0) {
                    continue;
                }
                tempNode = new OrthogonalNode(i, j);

                tempPreviousNode.nextOut = tempNode;
                tempPreviousNode = tempNode;
            }
        }

        //Step3 Link to its in nodes. This step is harder
        OrthogonalNode[] tempColumnNodes = new OrthogonalNode[numNodes];
        for (int i = 0; i < numNodes; i++) {
            tempColumnNodes[i] = headers[i];
        }
        for (int i = 0; i < numNodes; i++) {
            tempNode = headers[i].nextOut;
            while (tempNode != null) {
                tempColumnNodes[tempNode.column].nextIn = tempNode;
                tempColumnNodes[tempNode.column] = tempNode;

                tempNode = tempNode.nextOut;
            }
        }
    }

    @Override
    public String toString() {
        String resultString = "Out arcs: ";

        OrthogonalNode tempNode;
        for (int i = 0; i < numNodes; i++) {
            tempNode = headers[i].nextOut;
            while (tempNode != null) {
                resultString += " (" + tempNode.row + ", " + tempNode.column + ")";
                tempNode = tempNode.nextOut;
            }
            resultString += "\r\n";
        }
        resultString += "\r\nIn arcs: ";

        for (int i = 0; i < numNodes; i++) {
            tempNode = headers[i].nextIn;

            while (tempNode != null) {
                resultString += " (" + tempNode.row + ", " + tempNode.column + ")";
                tempNode = tempNode.nextIn;
            }
            resultString += "\r\n";
        }

        return resultString;
    }

    public static void main(String[] args) {
        int[][] tempMatrix = { { 0, 1, 0, 0 }, { 0, 0, 0, 1 }, { 1, 0, 0, 0 }, { 0, 1, 1, 0 } };
        OrthogonalList tempList = new OrthogonalList(tempMatrix);
        System.out.println("The data are:\r\n" + tempList);
    }

}