GPS定位原理

GPS卫星：

卫星定位系统是一种使用卫星对某物进行准确定位的技术，它从最初的定位精度低、不能实时定位、难以提供及时的导航服务，发展到现如今的高精度GPS全球定位系统，实现了在任意时刻、地球上任意一点都可以同时观测到4颗卫星，以便实现导航、定位、授时等功能。卫星定位可以用来引导飞机、船舶、车辆、以及个人，安全、准确地沿着选定的路线，准时到达目的地。卫星定位还可以应用到手机追寻等功能中。
卫星定位技术是利用人造地球卫星进行点位测量的技术。早期，人造地球卫星仅仅作为一种空间的观测目标，这种对卫星的几何观测能够解决用常规大地测量难以实现的远距离陆地海岛联测定位的问题。但是这种方法费时费力，不仅定位精度低，而且不能测得点位的地心坐标。
20世纪50年代末期美国研制的子午卫星导航系统（NNSS）为GPS的前身，用5到6颗卫星组成的星网工作，每天最多绕过地球13次，但无法给出高度信息，在定位精度方面也不尽如人意。但子午仪系统使得研发部门对卫星定位取得了初步的经验，并验证了由卫星系统进行定位的可行性，为GPS系统的研制埋下了铺垫，它开创了海空导航的新时代，揭开了卫星大地测量学的新篇章。

全球定位系统（GPS）是20世纪70年代由美国陆海空三军联合研制的新一代空间卫星导航定位系统。其主要目的是为陆、海、空三大领域提供实时、全天候和全球性的导航服务，并用于情报收集、核爆监测和应急通讯等一些军事目的，是美国独霸全球战略的重要组成。经过20余年的研究实验，耗资300亿美元，到1994年3月，全球覆盖率高达98%的24颗GPS卫星星座才布设完成。

全球定位系统（GPS）的24颗卫星中，其中21颗为工作卫星，3颗为备用卫星。24颗卫星均匀分布在6个轨道平面上，即每个轨道面上有4颗卫星。如下图所示，卫星轨道面相对于地球赤道面的轨道倾角为55°，各轨道平面的升交点的赤经相差60°，一个轨道平面上的卫星比西边相邻轨道平面上的相应卫星升交角距超前30°。这种布局的目的是保证在全球任何地点、任何时刻至少可以观测到4颗卫星。GPS卫星定位系统卫星轨道高度约为20200km，定位精度可以达到10m。

GPS的组成:

GPS（Global Positioning System，全球定位系统）包括三大部分：空间GPS卫星星座、地面监控系统、用户GPS信号接收机。GPS定位的基本原理为：卫星不断的发射自身的星历参数和时间信息，GPS信号接收机接收到信号后，根据三角公式计算可以得到接收机的位置，三颗卫星可进行2D定位（经度、纬度），四颗卫星则可进行3D定位（经度、纬度及高度）。通过接收机不断的更新接收信息，就可以计算出移动方向和速度。

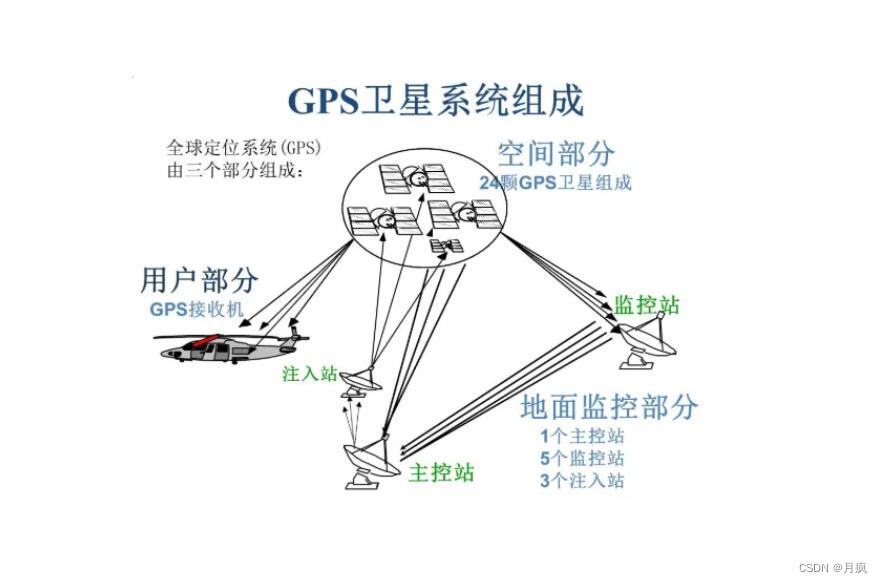为啥需要四颗卫星来定位？

电磁波传播速度也是光速3*10的8次方。定位最基本要求卫星和用户接收机都需要配备精确的时钟，卫星传送到地面的时间大约是0.06s左右。卫星上配备的原子钟（比较昂贵），精度比较高，用户的一半都比较低，为了降低成本。3D定位，需要精度，纬度和高度以及接收机钟差。四个未知数需要四个方程，就最少同时需要4个卫星接收到信号。

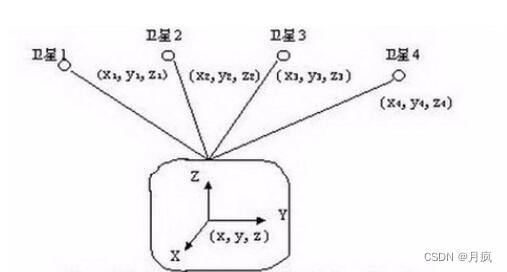
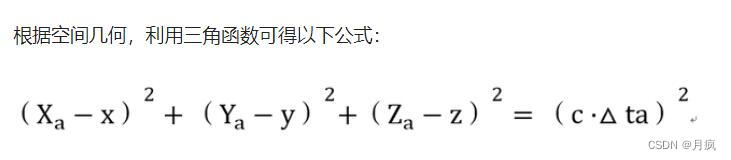
$\sqrt{(x1-x)^{2}+(y1-y)^{2}+(z1-z)^{2}} - c*(Vt1-Vt0) = 0$ d1

$\sqrt{(x2-x)^{2}+(y2-y)^{2}+(z2-z)^{2}} - c*(Vt2-Vt0) = 0$ d2

$\sqrt{(x3-x)^{2}+(y3-y)^{2}+(z3-z)^{2}} - c*(Vt3-Vt0) = 0$ d3

$\sqrt{(x4-x)^{2}+(y4-y)^{2}+(z4-z)^{2}} - c*(Vt4-Vt0) = 0$ d4

其中（x,y,z）就是用户的（经度，纬度，高度），d1、d2、d3、d4就是当前时间戳减去发射数据时候的时间戳，再乘以光速得到。Vt0是接受机接受到的时间，也是一个位置参数。Vt1、Vt2、Vt3、Vt4是卫星钟的钟差，这个是非常精确地，但是Vt0是接收机接收到的差异性很大，所以需要定位未知数。

这里比较麻烦，举个列子：

举例来说：用户要使用开车导航，卫星a为他服务。8:00:00卫星a发出了一个信号（含卫星坐标Xa、Ya、Za和时刻Ta=8:00:00），并以光速c到达地球。

假设用户的接收器——手机（坐标xyz）接到该信号时的时刻ta是8:00:02，那么△ta=8:00:02-8:00:00=2秒，两者距离La=c·△ta=60万公里（假设）。

但是，这里出现了一个致命问题：△t的确定，受到双方时间精准性的影响。

卫星上的时钟极其精准，Ta没有问题，但小章的手机很弱，上面的时钟精度很低，与标准时间有t0的误差（受限于制造成本，该误差难以消除，这是民用手机的通病）。导致我们以为小章的手机是8:00:02接到的信息，实际此时是8:00:01, △t应为1秒而不是2秒，再乘以光速c之后，误差会极其大，失之毫厘，谬以千里，定位会相差数公里，失去意义。

如何消除误差？这就需要引入第四颗卫星，来消除t0的影响。

校准卫星时差？

第四颗卫星的使用，就是为了多列一组方程，多求得一个未知数t0（手机时间误差），以此消除t0的影响，这即是校准时间。但是更加难校准的是卫星时间T。

默认卫星时间T非常精准，但由于受到狭义相对论和广义相对论影响，一天之内误差将累积到38微秒，如果不校准，再小的误差乘以光速c，也将成为难以估量的偏差，因此必须校准。

事实上，卫星上的时钟的精准程度，直接影响了定位精度，因此各个国家都是想尽一切办法使用高精度时钟，追求极致的精准，尽可能减小定位误差。比如GPS系统，从最开始使用石英振荡器、定位误差为14米，到后来使用铷原子钟和铯原子钟，误差分别缩小到8米和2.9米，而现在使用的氢原子钟，则使误差降到仅为1米。

定位的精确性？

SA政策是美国政府从其国家利益出发，通过降低广播星历精度（ε技术）、在GPS信号中加入高频抖动等方法，人为降低普通用户利用GPS进行导航定位时的精度的一种方法。普通GPS的信号有两种码，分别为C/A码和P码。C/A码的误差是29.3m到2.93米。一般的接收机利用C/A码计算定位。美国在90代中期为了自身的安全考虑，在信号上加入了SA (Selective Availability)，令接收机的误差增大，到100米左右。在2000年5月2日，SA取消，所以，咱们现在的GPS精度应该能在20米以内。而P码的误差为2.93米到0.293米是C/A码的十分之一，但是P码只能美国军方使用。

关于中国国内对GPS的一些规定？

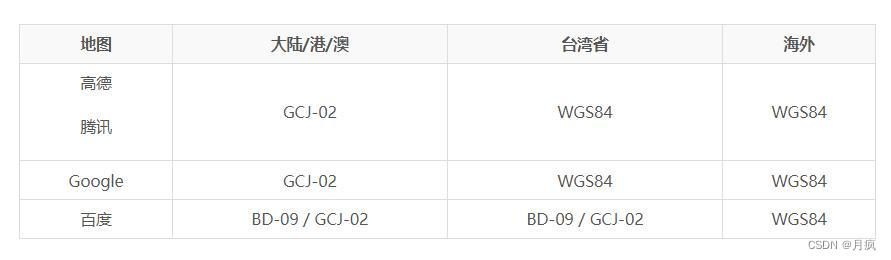
中国测绘局以国家安全为理由，用法律的形式对所有在中国发行的地图类产品加了强制性规范，要求所有地图类产品都必须使用国家测绘局的一种加偏移的算法（GCJ-02），对地图的真实坐标进行加偏移处理，之后才可能通过审批准许上市。因此，中国的所有官方及商用地图的坐标都是偏移的，这种偏移属于非线性的，偏移量在300至500米不等，偏移方向也不定。这种加过偏移的地图坐标就是所谓“火星坐标”。

WGS-84：是国际标准，GPS坐标（Google Earth使用、或者GPS模块）
GCJ-02：中国坐标偏移标准，Google Map、高德、腾讯使用（就是对GPS采集到的坐标信息进行加密处理，也就是火星坐标）
BD-09：百度坐标偏移标准，Baidu Map使用（百度对GCJ-02进行了二次加密处理）

中国使用GPS就会存在一些漂移问题？

1、偏移的起因：中国测绘局以国家安全为理由，用法律的形式对所有在中国发行的地图类产品加了强制性规范，要求所有地图类产品都必须使用国家测绘局的一种加偏移的算法，对地图的真实坐标进行加偏移处理，之后才可能通过审批准许上市。因此，中国的所有官方及商用地图的坐标都是偏移的，这种偏移属于非线性的，偏移量在300至500米不等，偏移方向也不定。这种加过偏移的地图坐标就是所谓“火星坐标”。
2、GPS接收机本身接收卫星的信号，计算出本机所在位置的经纬度，在没有做特别处理的时候，这个经纬度是正确的。但是如果GPS支持加载地图的话，这个GPS中的地图就得受上述第一条法规的约束了，所以正式在中国销售的行货GPS设备中的地图必须也得加偏移，处理成火星坐标。
3、问题来了，如果仅仅是地图搞成火星坐标，但GPS仍然输出真实坐标的话，就会发生GPS的定位（及导航）跟地图不能吻合的问题。于是，只好在GPS软件中设置一个使用同样算法的加偏移功能。GPS先从卫星上得到真实坐标，然后经过加偏移程序转换成火星坐标，由于是同一个算法，所以经过软件加偏移的坐标能跟同样加了偏移的地图吻合，就是“歪到一起”了。这样就可以用GPS正常导航了——但这台GPS设备输出的坐标仍然是火星坐标，放到Google Earth上面是没法正常吻合的。
4、由于Google Earth属于卫星照片，它不是地图，所以不受中国测绘法的约束，因此Google Earth的坐标是真实坐标。这样，问题又来了，当你使用中国处理过的GPS导出火星坐标（或航迹），企图把它放到Google Earth上面看看自己都走了哪些路的时候，因为Google Earth照片的坐标是真实的，而你的GPS导出的坐标是火星坐标，二者就对不上号了，你也许会看到在google Earth上，你开着车从别人的楼顶上飞过去，或者打湖里面漂过去。
5、水货GPS因为是洋鬼子的产品，原本并非销往中国的，洋鬼子不会玩这种加偏移的买卖，所以水货GPS设备，如果使用机器原带的地图的话，得到的坐标（或者航迹）是真实正确的，这就是水货机器的无偏地图。但是洋鬼子的设备中一般没有中文地图，如果你把中国的官方或者正式发布的商用地图放到水货GPS设备里面的话，就会发生第3条前面说的问题：设备的真实坐标跟天朝特殊地图的火星坐标不吻合——出现偏移——无法正常导航。
6、由于火星坐标的一系列问题，众民间人士根据那个加偏移算法自行折腾出了很多纠正了偏移的地图，这些地图的坐标是正确的。这样的地图拿到水货GPS设备上，因为水货GPS输出的坐标是真实的，所以可以完美配合工作，正确导航定位，并且输出正确的坐标——放到Google Earth上也是正确的。
7、中国行货GPS设备软件中的加偏移功能，是通过一个所谓空心地图文件（或者28类地图，或者快拼模块）来触发启动偏移程序的，如果用户安装非本机自带的，但属于中国官方或者正式发布的商用地图，那要配合空心地图文件（或者把地图类别设置为28），从而让GPS软件中的加偏移程序启动，使得GPS输出火星坐标，跟地图的火星坐标吻合，如此才能正常导航——但这台GPS设备输出的坐标仍然是火星坐标，放到Google Earth上面是没法正常吻合的。
8、中国行货GPS设备，如果要得到真实坐标，使用民间的纠偏地图，就得把那个空心地图文件移除（或把原机自带的28类地图移除/取消，或把同样作用的快拼弄掉），这样GPS设备输出真实的坐标，才能跟纠偏地图的正确坐标吻合，实现正确导航定位，并且输出正确的坐标——放到Google Earth上也是正确的。不过，在天朝行货GPS上不能同时使用火星坐标地图和纠偏地图，否则必然有一个没法正常导航定位。
9、水货GPS设备用民间的简体中文刷机，一般来说也没有那个加偏移程序，所以要使用纠偏地图或者无偏地图。不能使用天朝官方的火星坐标地图，不然就对不上号。

如何处理GPS漂移呢？

1）纯软件方法。

通过软件滤波算法在设备里或者在定位平台上进行过滤。这种方法是早期用的较多的方法，因为代价小，灵活。

缺点:由于模型的复杂度和场景的不稳定性，软件过滤会必然损失有效数据的细节，有无无法覆盖所有的特征场景，特殊场景下无作用。

1、查表

2、纠偏接口，网络获取（第三方接口）

3、自己写纠偏算法Java和C#应用PC和ANDROID

2）自身硬件调节。

很多产品为了强调自己的定位快，调大了接收灵敏度，带来的一个副作用就是严重漂移。车辆行驶时还好，基本看不粗来有什么影响，因为有强有效信号抑制作用，一旦等红灯或者在一个地方长时间停留，就会产生很大的漂移，出现莫名其妙的轨迹，严重的可影响正常使用。处理方法，通过信号通道的前端匹配，适当降低灵敏度，就可以改善gps漂移。

缺点：GPS冷启动时间变长。

3) 第三方传感器辅助。

通过第三方的传感器数据，对gps的数据进行筛选和修正。这种方法在高配机型中较常见，是目前主流的方法，集合软件算法的精髓和硬件的专业性，同时不损失GPS的指标。

缺点：需要增加额外硬件成本，同时增加了开发复杂性。

针对上面情况的出现，我们使用软件处理漂移问题？

0、先了解一些地理知识

纬度划分：自赤道开始向南、向北各划分为90°，向南为南纬，向北为北纬。

经度划分：自本初子午线开始向东、向西各划分180°，向东为东经度，向西为西经度。

经纬度是经度与纬度的合称组成一个坐标系统。经度是地球上一个地点离一根被称为本初子午线的南北方向走线以东或以西的度数。

纬度是指某点与地球球心的连线和地球赤道面所成的线面角，其数值在0至90度之间。经纬度是经度与纬度的合称组成一个坐标系统。又称为地理坐标系统。

1、如何通过GPS经纬度计算地球半径

假设地球是一个完美的球体，它的半径就是地球的平均半径R=6371.004km，如果以0度经线为基准，那么根据地球表面任意俩点的经纬度就可以计算出这俩点间的距离。
反过来，通过实地测量俩个位置间的距离D，可以通过响应的经纬度推算地球半径R。
俩个点的坐标位置A（MLonA，MLatA），B（MLonB，MLatB）根据三角推导，可以计算出来俩点相对地轴的角度的公式。

C=sin(MLatA)*sin(MLatB)*cos(MLonA-MLonB)+cos(MLatA)*cos(MLatB)
弧度AB(D)=R*arccos(C)
推算出半径R，有：
R=D/arccos(C)

注释：反三角函数中的反余弦arccos(C)值域为[0，π]

弧长计算公式是一个数学公式，为L=n× π× r/180，L=α× r。其中n是圆心角度数（角度制），r是半径，L是圆心角弧长，α是圆心角度数（弧度制）

扇形的弧长=2πr×角度/360

扇形面积公式：S（扇形面积）=nπR^2/360

小注意：

圆锥的表面积=圆锥的侧面积+底面圆的面积
其中：圆锥体的侧面积=πRL
圆锥体的全面积=πRL+πR²

2、一些坐标转换关系（编程）

//GPS 偏移校正(WGS-84) 到(GCJ-02) java版本实现

//GPS 偏移校正(WGS-84) 到(GCJ-02) java版本实现：
    public class ChinaGPS {
        final static double pi = 3.14159265358979324; //圆周率π
        final static double a = 6378245.0;   //地球半径是a米
        final static double ee = 0.00669342162296594323;//扁率
        /**
         * 直接传入经纬度
         * @param wgLat 经度
         * @param wgLon 纬度
         * @return
         */
        public static double[] transform(double wgLat, double wgLon)
        {
            double mgLat=0;
            double mgLon=0;
            if (outOfChina(wgLat, wgLon)) //是否超出中国范围
            {
                mgLat = wgLat;
                mgLon = wgLon;

            }else{
                double dLat = transformLat(wgLon - 105.0, wgLat - 35.0);
                double dLon = transformLon(wgLon - 105.0, wgLat - 35.0);
                double radLat = wgLat / 180.0 * pi;
                double magic = Math.sin(radLat);
                magic = 1 - ee * magic * magic;
                double sqrtMagic = Math.sqrt(magic);
                dLat = (dLat * 180.0) / ((a * (1 - ee)) / (magic * sqrtMagic) * pi);
                dLon = (dLon * 180.0) / (a / sqrtMagic * Math.cos(radLat) * pi);
                mgLat = wgLat + dLat;
                mgLon = wgLon + dLon;
            }
            double[] point={mgLat,mgLon};
            return point;
        }
        //判断是否在中国国内，在国内做GPS漂移，不在国内不做GPS漂移
        private static boolean outOfChina(double lat, double lon)
        {
            if (lon < 72.004 || lon > 137.8347)
                return true;
            if (lat < 0.8293 || lat > 55.8271)
                return true;
            return false;
        }
        private static double transformLat(double x, double y)
        {
            double ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y + 0.2 * Math.sqrt(Math.abs(x));
            ret += (20.0 * Math.sin(6.0 * x * pi) + 20.0 * Math.sin(2.0 * x * pi)) * 2.0 / 3.0;
            ret += (20.0 * Math.sin(y * pi) + 40.0 * Math.sin(y / 3.0 * pi)) * 2.0 / 3.0;
            ret += (160.0 * Math.sin(y / 12.0 * pi) + 320 * Math.sin(y * pi / 30.0)) * 2.0 / 3.0;
            return ret;
        }
        private static double transformLon(double x, double y)
        {
            double ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1 * Math.sqrt(Math.abs(x));
            ret += (20.0 * Math.sin(6.0 * x * pi) + 20.0 * Math.sin(2.0 * x * pi)) * 2.0 / 3.0;
            ret += (20.0 * Math.sin(x * pi) + 40.0 * Math.sin(x / 3.0 * pi)) * 2.0 / 3.0;
            ret += (150.0 * Math.sin(x / 12.0 * pi) + 300.0 * Math.sin(x / 30.0 * pi)) * 2.0 / 3.0;
            return ret;
        }
}

先就列这一个网上有大部分的坐标转换算法，大同小异吧。

3、下来说说我们把这些都做了，但是还是有很大误差，需要软件算法介入的一些方法