先把自己写完的总结一下：
题目一：
猫儿园的告示牌上贴着 a×b 大小的矩形广告纸。猫猫对广告不感兴趣，她想知道能否用 c×d 的矩形白纸完全覆盖这个广告。猫猫可以对白纸进行平移、旋转，但不能折叠或撕开等。如果可以完全覆盖输出 YES，否则输出 NO。
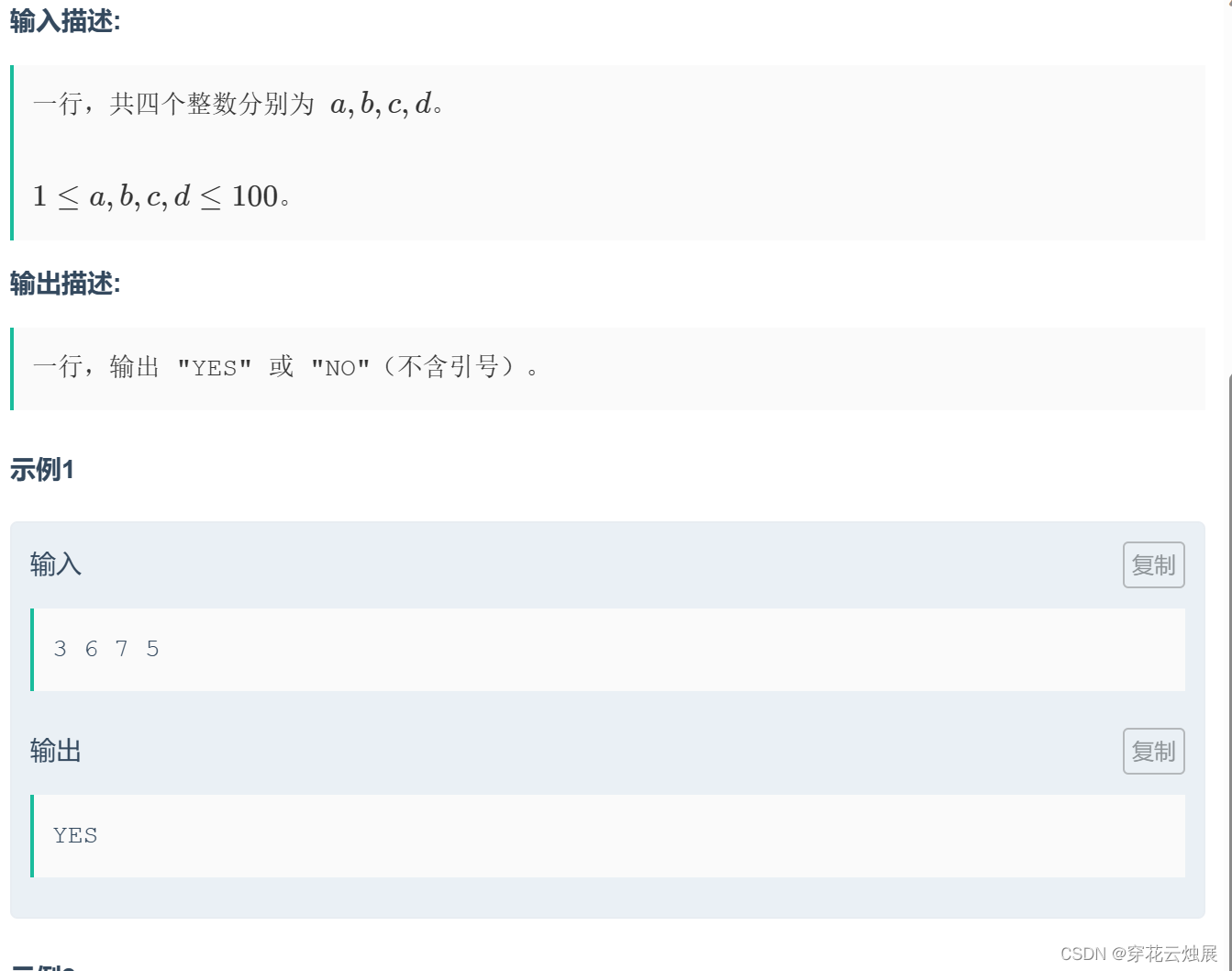
代码是这样的：
#include<stdio.h>
int main()
{
int a,b,c,d;
scanf("%d %d %d %d",&a,&b,&c,&d);
if((a<=c&&b<=d)||(a<=d&&b<=c))printf("YES\n");
else{
printf("NO\n");
}
return 0;
}。本来我想的是只要每个长宽分别大于等于另一个的长宽就可以了，其实如果刚好这个长没有大于等于这个长的话，但是这个宽大于等于，并且这个长又正好大于等于另一个的宽，就也可以所以包含两种情况，我说的这个是指用来覆盖的矩形；
题目二：
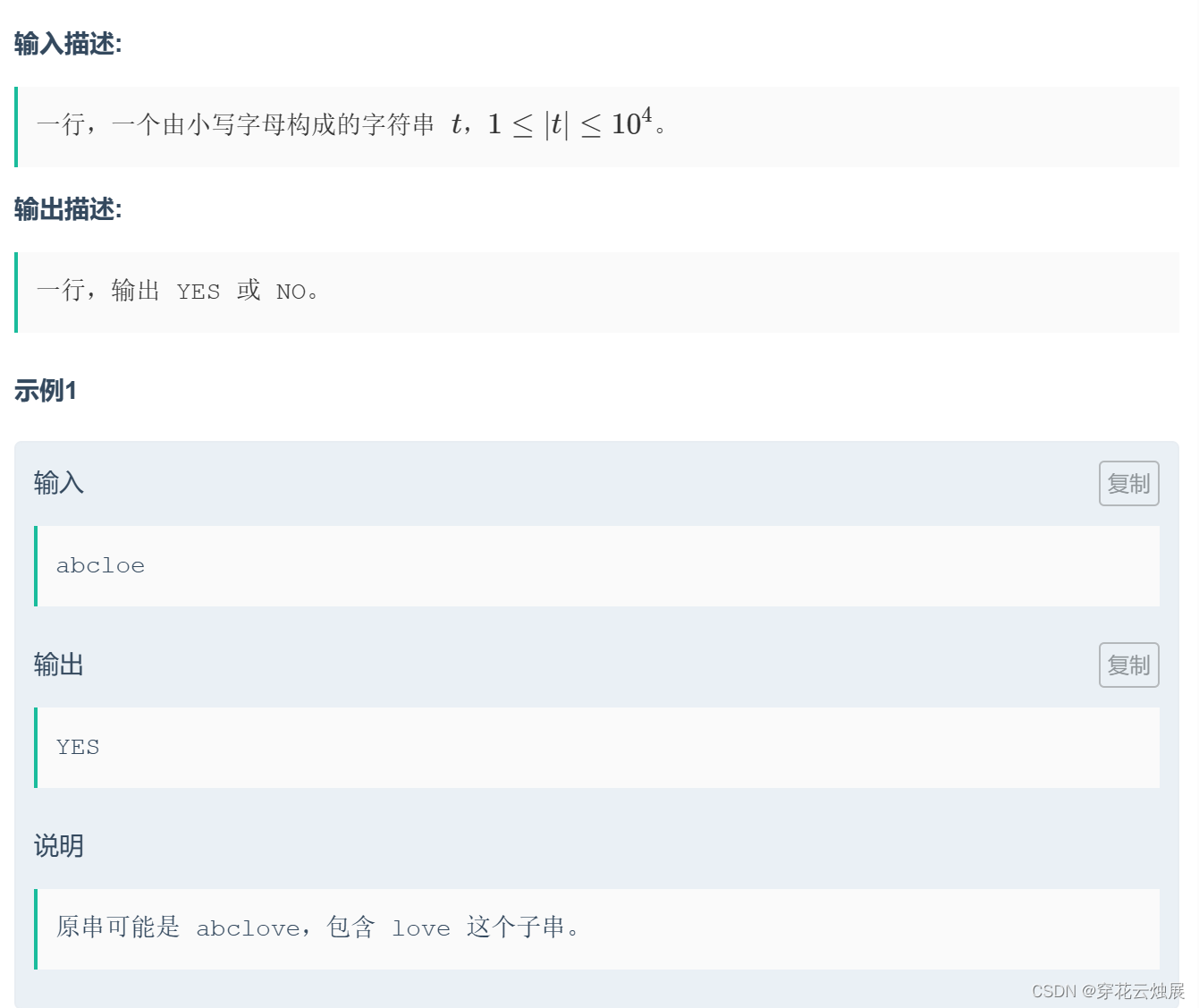
猫猫的电子邮箱中收到了一封密信，内容为一个由小写字母构成的字符串 
由于电脑故障，某个字符突然消失了，前后两部分 (可能为空) 拼接成了一个新的字符串 t。形式化地，假设 si 消失了，则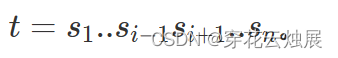
。现在给定 t，猫猫想知道 s 中是否有可能存在 "love" 这个子串（不含引号）。如果有可能，输出 YES，否则输出 NO。
子串的定义为：一个字符串中连续的若干字符形成的新字符串。
代码：
一看这题我满脑子都是直接列出情况，这里情况较少，是可以的，及时break可以节约时间，由于这里只问有没有，一旦找到就说明有了，就可以不用去遍历整个字符串了，但是要谨防数组越界，所以要在循环的最开头写上当到倒数第二个还没有结束的话就已经没有了；
#include<stdio.h>
#include<string.h>
char a[10001];
int main()
{
scanf("%s",a);
for(int i=0;i<strlen(a);i++)
{
if(i+2==strlen(a)){printf("NO\n");break;}
if(a[i]=='o'&&a[i+1]=='v'&&a[i+2]=='e'){printf("YES\n");break;}
if(a[i]=='l'&&a[i+1]=='v'&&a[i+2]=='e'){printf("YES\n");break;}
if(a[i]=='l'&&a[i+1]=='o'&&a[i+2]=='e'){printf("YES\n");break;}
if(a[i]=='l'&&a[i+1]=='o'&&a[i+2]=='v'){printf("YES\n");break;}
}
return 0;
}题目三：
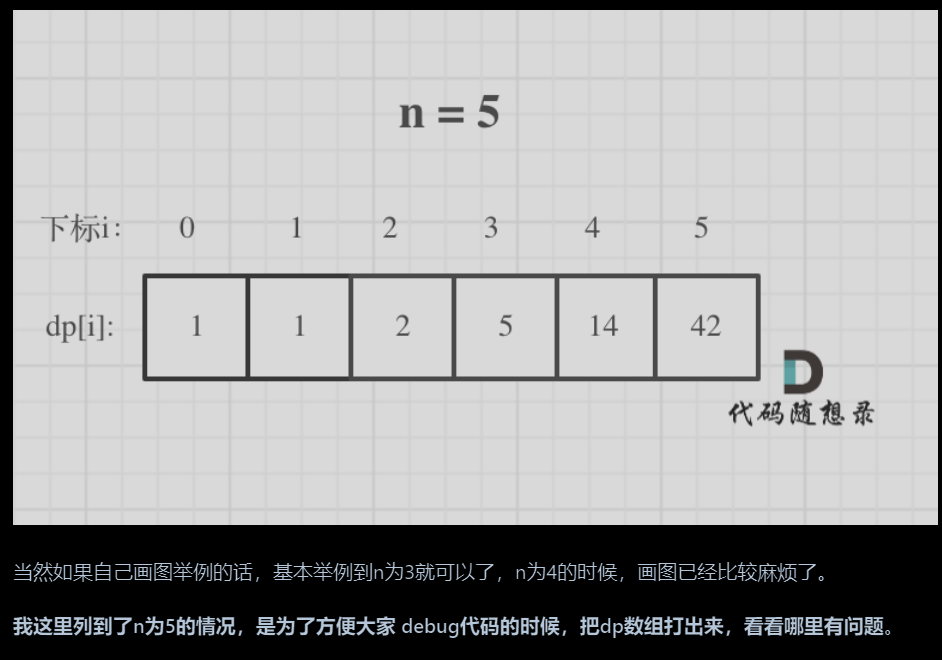
猫猫发现了一个数列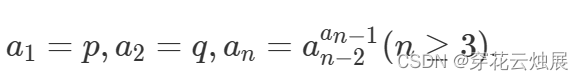
为了防止数据溢出，猫猫想让你找到最大的正整数 n,an≤M,其中M=10^18，可以证明一定有解。
输入描述:
输出描述:
一行，一个整数，表示答案。
示例1
输入
复制2 2
2 2
输出
复制5
5
示例2
输入
复制999999998 2
999999998 2
输出
复制3
3
这个题目我刚开始写个时候就在疯狂找规律，然后想着把所有的情况列出来，然后暴力求解，最后情况一直没有列全；然后我又想到可以直接求，反正数字不是很大，可以直接求，然后我就把这一串代码交上去了：
#include<stdio.h>
#include<math.h>
int main()
{
const long long mm=10e18;
long long a,b;
scanf("%d %d",&a,&b);
int h=2;
while(pow(a,b)<=mm)
{
long long t=a;
a=b;
b=pow(t,a);
h++;
}
printf("%d\n",h);
return 0;
}
突然发现这个也可以过加一个把d变成lld
#include<stdio.h>
#include<math.h>
int main()
{
const long long mm=10e18;
long long a,b;
scanf("%lld %lld",&a,&b);
int h=2;
while(pow(a,b)<=mm)
{
long long t=a;
a=b;
b=pow(t,a);
h++;
}
printf("%d\n",h);
return 0;
}
变成对数就好算了：
代码是这样的就过了：
#include<stdio.h>
#include<math.h>
int main()
{
const long long mm=10e18;
long long a,b;
scanf("%d %d",&a,&b);
int h=2;
while(b*log(a)<=log(mm))
{
long long t=a;
a=b;
b=pow(t,a);
h++;
}
printf("%d\n",h);
return 0;
}
但是这样写还是会有误差。由于这个取对数函数取出来是小数，但是误差不大，所以在这个题里面没有写误差的话也可以过，但是这里还是写一下：
#include<stdio.h>
#include<math.h>
int main()
{
const long long mm=10e18;
long long a,b;
scanf("%lld %lld",&a,&b);
int h=2;
const double k=1e-5;
while(b*log(a)<=log(mm)+k&&pow(a,b)<=mm)
{
long long t=a;
a=b;
b=pow(t,a);
h++;
}
printf("%d\n",h);
return 0;
}
这个误差是k比喻很小，至于为什么要加在后面呢？我认为，越大的数开出来的小数误差就越大，就越容易变小，所以加在这个大的后面，这就解决了这个小bug，但是还有一个bug，如果有刚开始的pq本身就比后面的大的话，那么这时候刚好由于它损失的也大，但是又因为后面的误差加了一下的话就让它小了起来刚好满足这个条件，这时候就体现了后面的再次判断的功能了，这时候明显发现前面的大，不满足条件循环结束；这样就使得逻辑完美了；
这里再补充一下关于log函数，log（10）表示以e为底十为真数的对数，求出来是小数，log2（6）表示以2为底6为真数的对数；这样就好理解上面的了；当然别忘了加上数学的头文件；
当时我有一个非常疑惑的点就是为什么输入a，b的时候这里用%d就不行（过不了），上面的就可以，其实可以这样理解，这个ab的输入都是没有超过int范围的啊；就很疑惑QAQ；
还有一个题，也是我写的最久的：
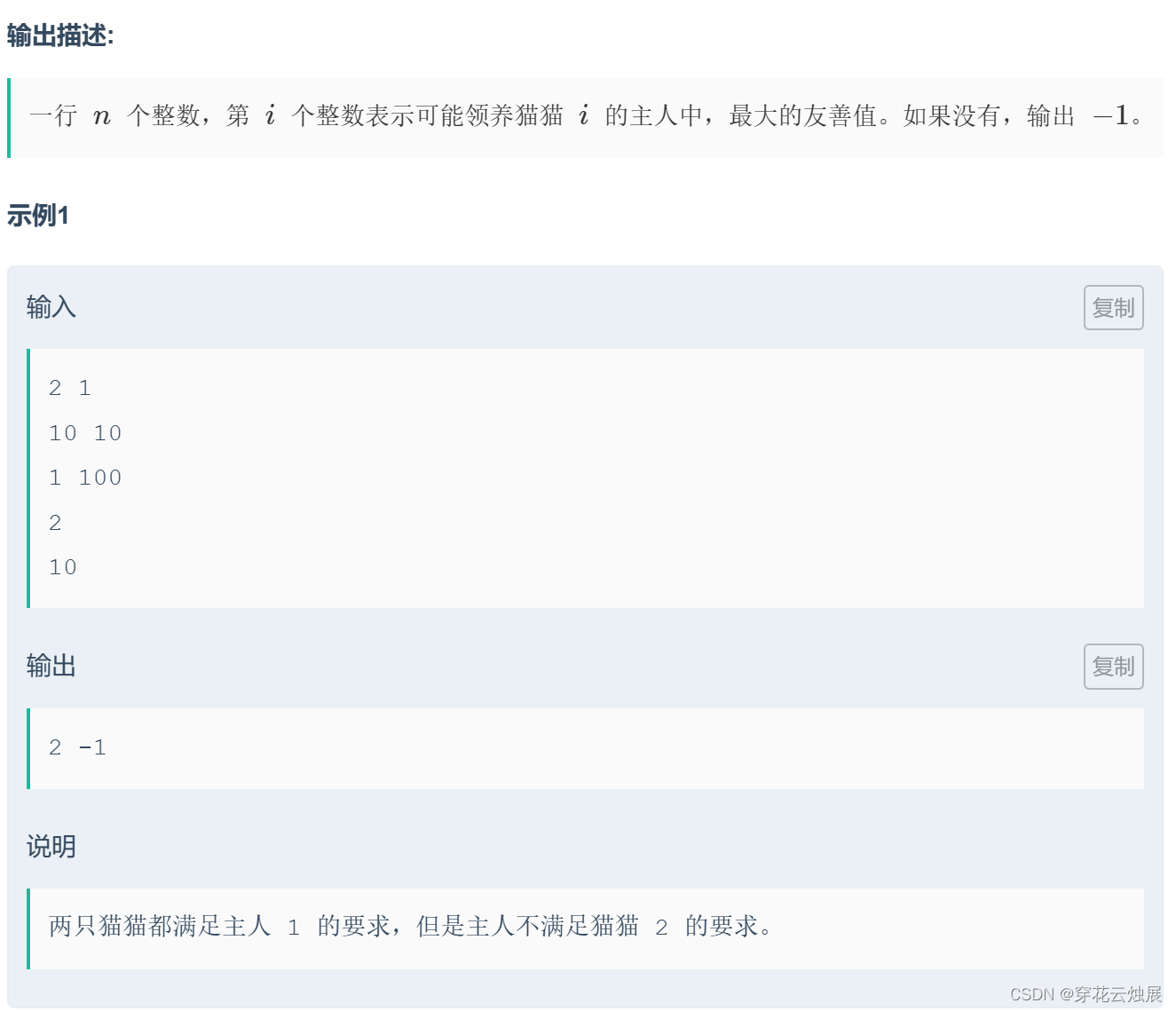
然后看了别人的代码还没搞出来；之后专门用一篇来记录这个题解QAQ：
希望你一如既往的坚强 ，站在迎着光的地方， 活成自己想要的模样 ；）
