假设ofdmN个子载波之间是完全正交的,即不考虑ICI影响,通过发送训练序列来实现信道估计。


其中,在推导6.8的时候,需要将6.6先拆解一下。
X
−
1
Y
=
X
−
1
(
X
H
+
Z
)
=
X
−
1
X
H
+
X
−
1
Z
=
H
+
X
−
1
Z
X^{-1}Y = X^{-1}(XH+Z) = X^{-1}XH +X^{-1}Z = H+X^{-1}Z
X−1Y=X−1(XH+Z)=X−1XH+X−1Z=H+X−1Z
所以公式6.8中的第2行可以进一步等价表示为
E
{
(
H
−
H
−
X
−
1
Z
)
H
(
H
−
H
−
X
−
1
Z
)
}
=
E
{
(
X
−
1
Z
)
H
(
X
−
1
Z
)
}
E\left\{(H-H-X^{-1}Z)^H(H-H-X^{-1}Z)\right\} = E\left\{(X^{-1}Z)^H(X^{-1}Z)\right\}
E{(H−H−X−1Z)H(H−H−X−1Z)}=E{(X−1Z)H(X−1Z)}
OFDM-LS信道估计 MMSE信道估计公式推导
news2026/2/15 17:32:26
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/457841.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
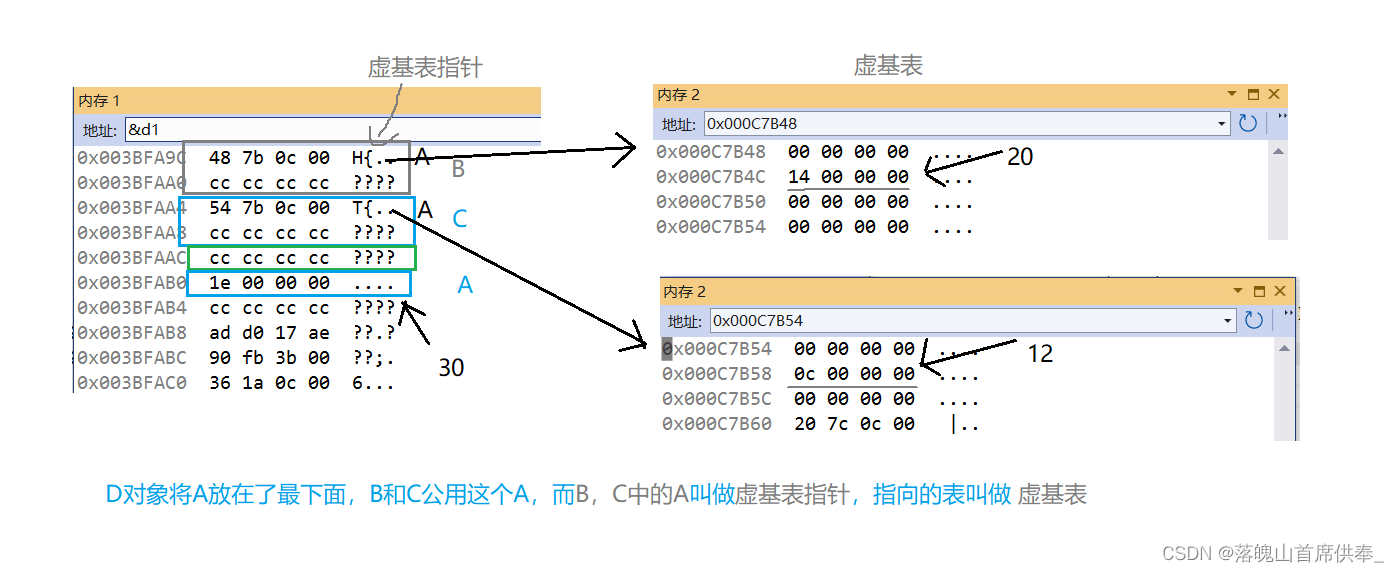
【难学易用c++ 之 继承】
目录: 前言一、继承的概念及定义(一)概念(二)继承定义继承关系和访问限定符继承基类成员访问方式的变化 二、基类和派生类对象赋值转换三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员七…
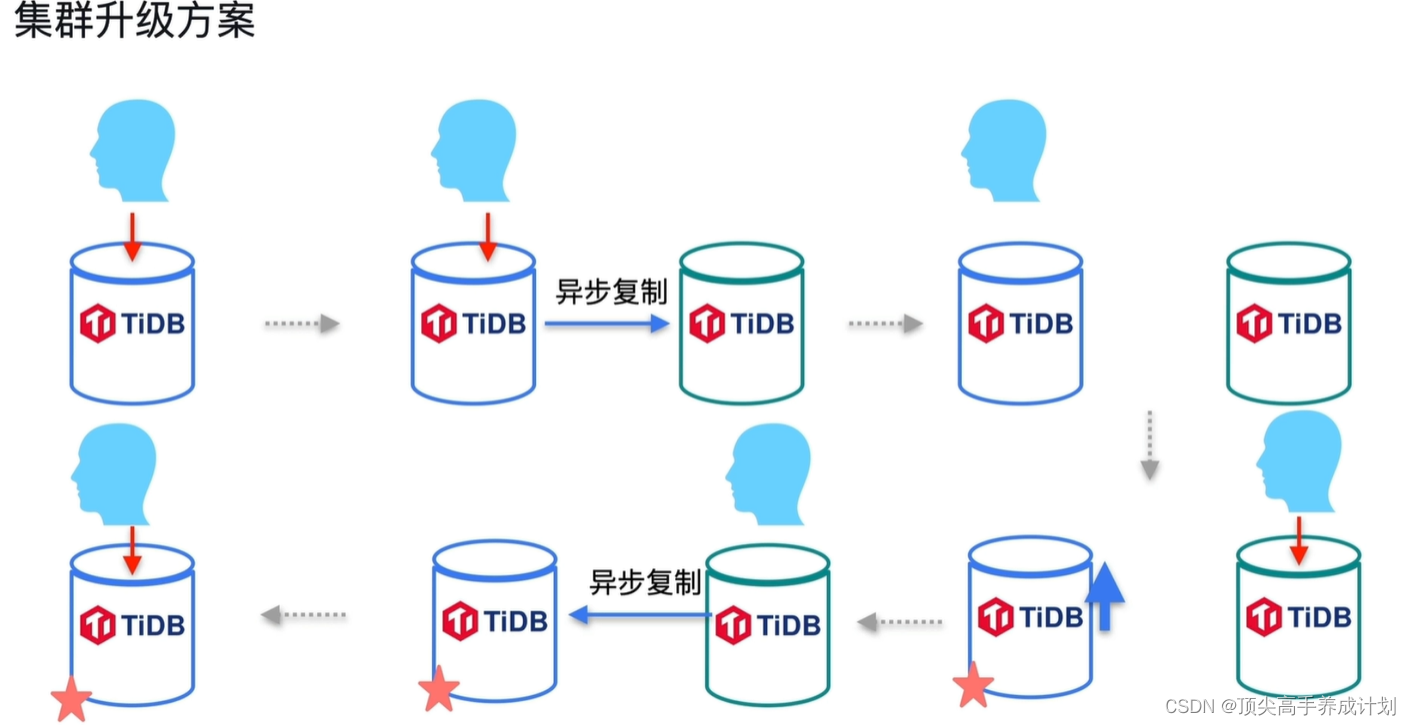
TiDB实战篇-常用的高可用架构
简介
TiDB实战篇-常用的高可用架构。
高可用要考虑的问题 同城三中心 RTO<35秒 RPO0(因为一个数据中心挂点了,还有其他两个可以提供服务)
(优点)数据副本不能在同一个数据中心(raft多数存活)(PD的label标签能够解决这个问题…
OpenCV基础之常见的图像梯度算子
文章目录 OpenCV基础之常见的图像梯度Roberts交叉算子Prewitt算子Sobel算子Laplacian算子 OpenCV基础之常见的图像梯度
梯度是一个向量,梯度方向指向函数变化最快的方向,大小就是它的模,也是最大的变化率。 图像梯度是指在图像中某个位置处沿…
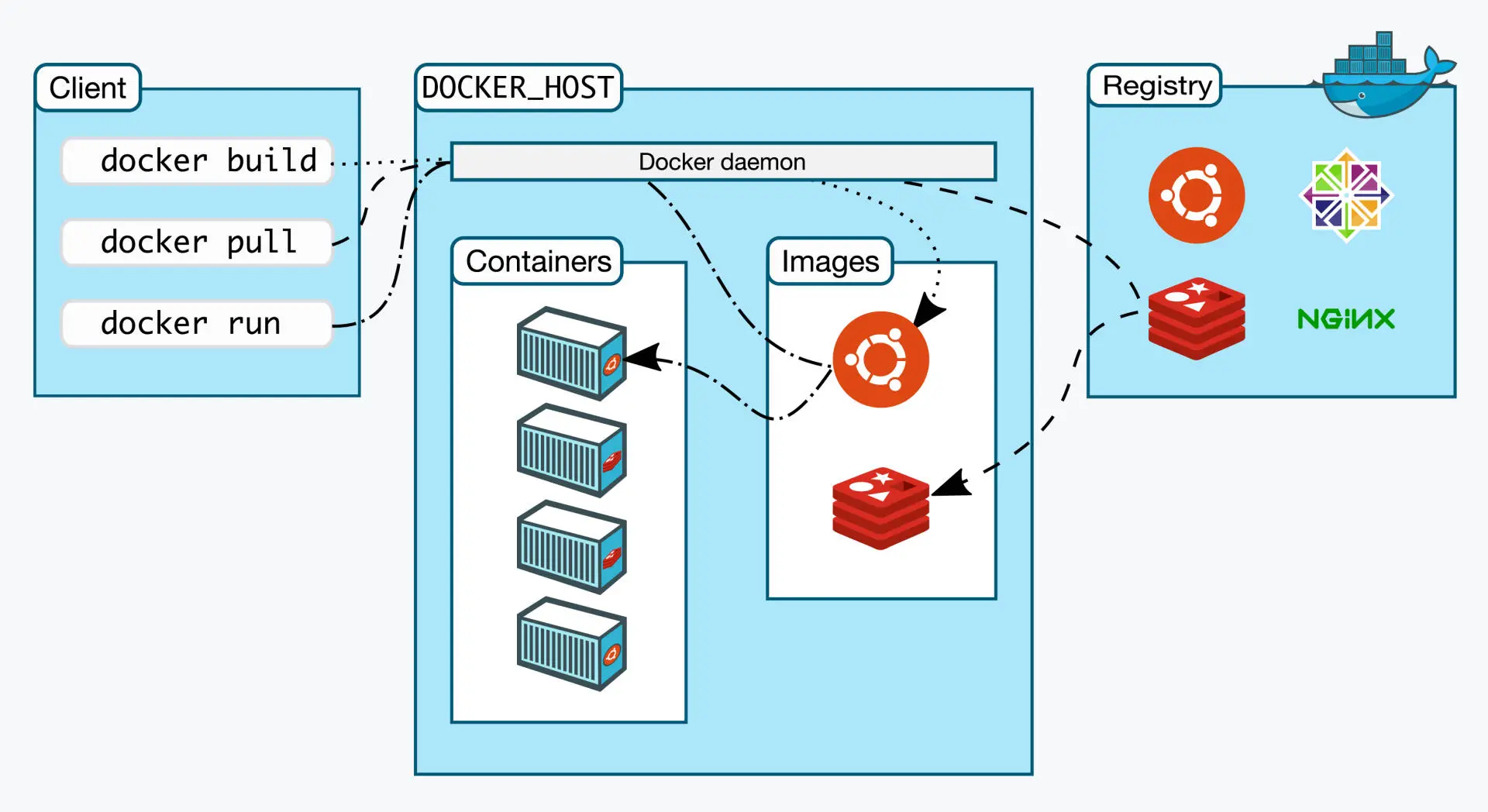
关于容器(Docker)的形象比喻
1 将容器比喻为样板间
容器是一种特殊的进程
容器依赖与Linux操作系统内核的几项技术:namespace、cgroup、chroot
namespace 与编程语言里的 namespace 有点类似,它可以创建出独立的文件系统、主机名、进程号、网络等资源空间,相当于给进程…
回归问题(Regression)
Regression 前言Dependent vs. Explanatory VariablesHandle Numerical Labelssquared error和variance什么区别 Linear RegressionLinear Regression in 1 Dimension Least Squares (最小二乘,重点)Least Squares ObjectiveMinimizing a Dif…
确保软件项目成功——验收测试指南
确保软件项目成功——验收测试指南 在软件项目验收测试中,软件测试报告是非常重要的一部分,需要准备和提交。以山东省在2021印发的《政府采购履约验收管理办法》为例: 省级各国家机关、事业单位和团体组织(以下统称“采购人”&…
会话跟踪——JWT令牌
会话指的是浏览器与服务器之间的一次连接,我们称之为一次会话。 在用户打开浏览器第一个访问服务器的时候,这个会话就建立了,只要有任何一方断开连接,此时会话就结束了。再一次会话中是可以包含多次请求和相应。那什么是会话跟踪呢…
动力节点springsecurity笔记14~18SpringSecurity 集成thymeleaf
15 SpringSecurity 集成thymeleaf
此项目是在springsecurity-12-database-authorization-method 的基础上进行 复制springsecurity-12-database-authorization-method 并重命名为springsecurity-13-thymeleaf
15.1 添加thymeleaf依赖
|
<groupId>org.springframewor…
vue3+vite3+typescript使用wangEditor编辑器
文章目录 ⭐写在前面⭐步入正题🚀1.安装🚀2.配置2.1 存数据2.2 读数据 🚀3.跨域及其他问题3.1 跨域3.2 其他问题 🚀4.写在最后 ⭐写在前面
🚀 框架Vue3 Vite3 TypeScript:
👉 Vue3ÿ…
地铁站人流检测硬件部分
目录
一、概述
二、驱动程序
2.1debug串口
2.2体重传感器HX711
2.3滴答定时器
2.4ESP8266
2.5人体检测
2.6 IIC的GPIO
2.7 OLED的IIC
2.8 LED
三、应用
四、中断 一、概述
使用STM32C8T6作为主控
A9 ---> tx(调试串口)
A10 ---> …
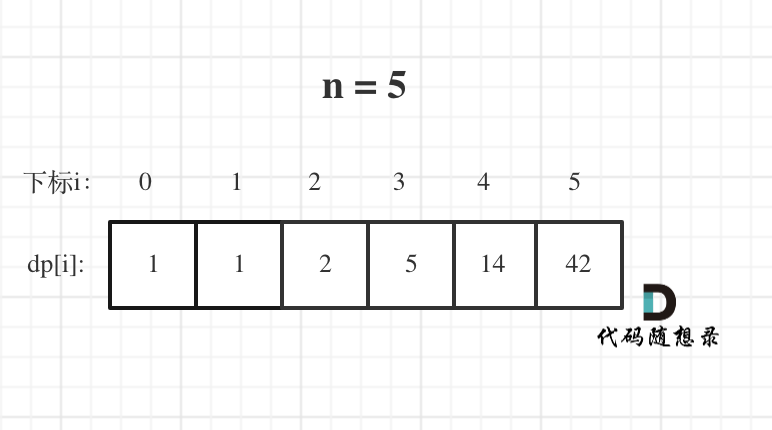
算法训练 Day41 | 动态规划
343. 整数拆分
思路: 确定dp数组(dp table)以及下标的含义:dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。 确定递推公式:dp[i] max(dp[i], max((i - j) * j, dp[i - j] * j)) 可以想 dp[i]最…
【python装饰器:看懂这10个例子你就掌握了!】
基本说明
Python 装饰器是一种函数,它可以用来修改其他函数的功能。它是 Python 中的一项高级编程技术,也是 Python 中比较重要的语法之一。
简单来说,装饰器就是一个函数,它可以接受一个函数作为参数,并返回一个函数…
Obsidian+坚果云+FolderSync解决电脑端和安卓端同步方案
目录1.Obsidian电脑端准备
2.Obsidian安卓端准备
3.坚果云电脑端准备
4.坚果云手机端准备
5.FolderSync手机端准备
6.百度云冗余备份 1.Obsidian电脑端准备
这里以windows版本为例,下载后安装
1.Obsidian官网:https://obsidian.md/ 官网下载有时候…
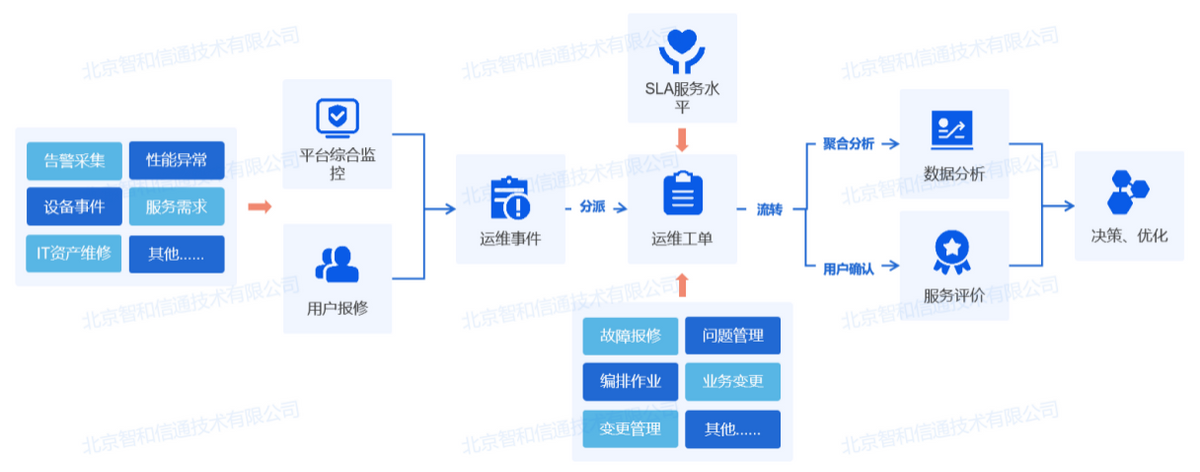
电力电网行业IT运维方案
智能电网背景下,电力、电网企业信息化逐渐渗透到其业务链的各个环节,云计算、物联网、移动互联网等新技术的应用,更驱动信息化与业务创新深度融合。电力、电网企业集团信息系统群逐渐朝着一体化方向发展,信息链越来越长࿰…
银行数字化转型导师坚鹏:宏观经济趋势与资本行业机遇和挑战
2023年宏观经济趋势与资本行业机遇和挑战 课程背景:
很多学员存在以下问题:
不知道我国目前的宏观经济形势?
不清楚宏观环境对我国经济的影响?
不知道资本行业未来主要发展趋势?
课程特色:
精彩解…
基于php的校园校园兼职网站的设计与实现
摘要
近年来,信息技术在大学校园中得到了广泛的应用,主要体现在两个方面:一是学校管理系统,包括教务管理、行政管理和分校管理,是我国大学管理和信息传递的主要渠道。二是学生生活服务平台。而随着大学生毕业人数的年…
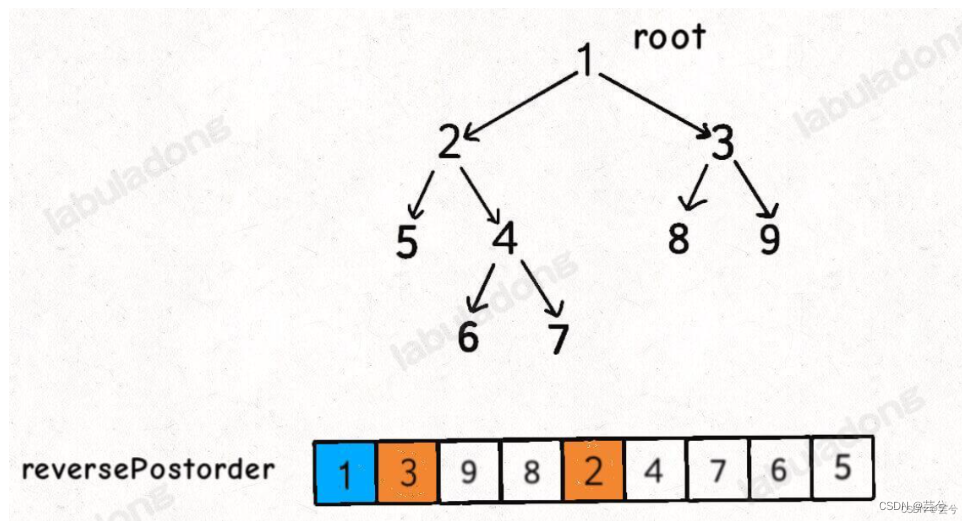
leetcode重点题目分类别记录(四)图论深入
文章目录 入度出度最大网络秩可以到达所有点的最少点数目 并查集省份数量等式方程的可满足性按字典序排列最小的等效字符串以图判树 二分图判断二分图 深度优先搜索封闭岛屿数量太平洋大西洋水流问题 广度优先搜索树上逃逸最短路径多源最短路径 拓扑排序DFS解决拓扑排序BFS解决…
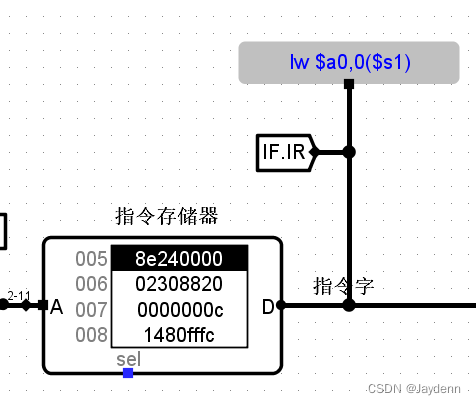
MIPS指令集-mars-cpu
MIPS通用寄存器
MIPS有32个通用寄存器($0-$31),各寄存器的功能及汇编程序中使用约定如下:
下表描述32个通用寄存器的别名和用途 REGISTER NAME USAGE $0 $zero 常量0(constant value 0) $1 $at 保留给汇编器(Reserved f…
K近邻算法(手写代码+图像识别实践)
k近邻算法作为一个分类算法,他通过计算不同特征值之间的距离来进行分类,它的工作原理是存在一个样本集合作为训练样本集,且每个样本都存在一个标签,此时,输入一个新的样本不存在标签,我们通过计算这个新样本…
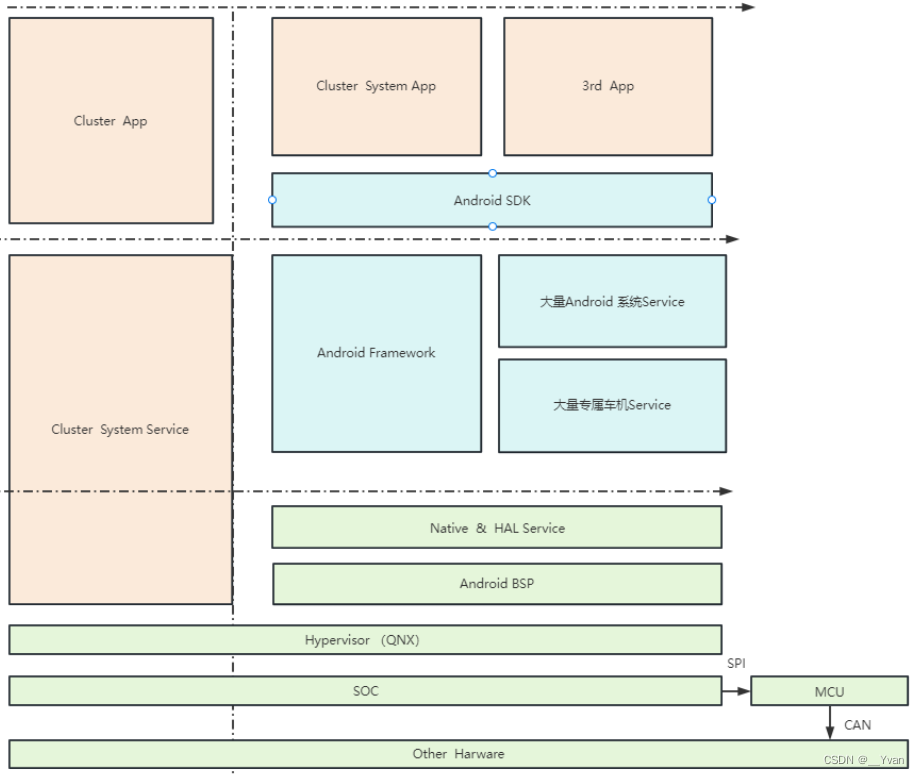
【Android车载系列】第10章 系统服务-SystemServer源码分析(API28)
1 SystemServer启动
&emps;&emps;SystemServer进程启动,首先从SystemServer.java文件的main()方法开始。
290 /**
291 * The main entry point from zygote.
292 */
293 public static void main(String[] args) {
294 new SystemSe…