343. 整数拆分

• 题目链接：代码随想录

本题就是一个个递推，通过将dp[i]定义为第i个值的最大乘积
然后最大乘积有两种来源，一个是(i - j) * j 还有一种是dp[i - j] * j;

• 解题思路：
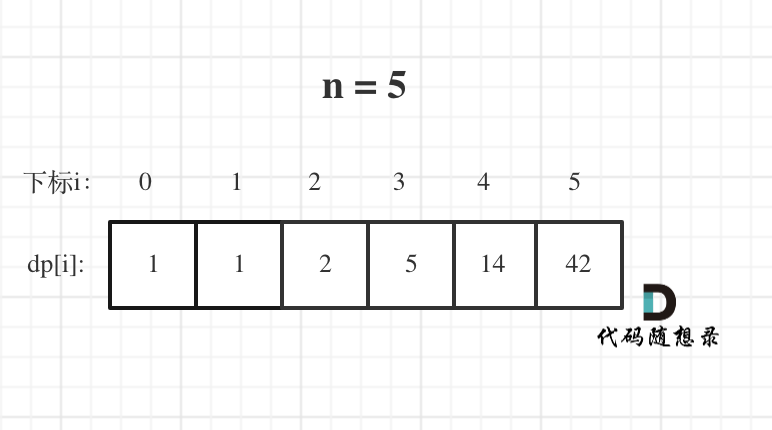
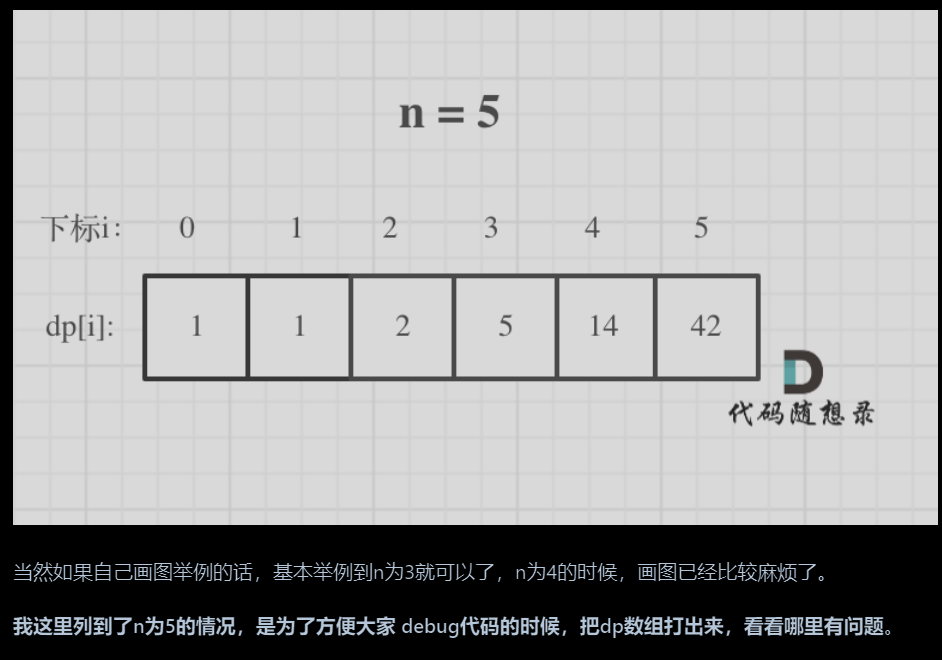
  1.确定dp数组（dp table）以及下标的含义。dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。
  2.确定递推公式dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));//这里不断更新dp[i]的值
  3.只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1
  4.dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]

• 推导过程

  

public int integerBreak(int n) {
    //dp[i]表示i的最大乘积
    int[] dp = new int[n + 1];

    //初始化2的最大乘积为1
    dp[2] = 1;

    for (int i = 3; i <= n; i++) {

        for (int j = 1; j < i; j++) {
            dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));
        }

    }

    return dp[n];
}

96.不同的二叉搜索树⭐️

• 题目链接：代码随想录

重点在于递推公式的推导以及利用二叉搜索树已经排好序的性质解题

• 递推公式推导

  

• 解题思路：
  1.dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]
  2.递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
  3.初始化：从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，因此初始化dp[0] = 1
  4.遍历顺序：首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

• 推导过程

  

public int numTrees(int n) {
    int[] dp = new int[n + 1];

    //初始化
    dp[0] = 1;
    for(int i = 1;i <= n;i++){
        //j用来确定不同的i不同的情况
        //j变量即以j作为头结点的求i的情况，每一次循环都是加上不同的情况
        for(int j = 1;j <= i;j++){
            dp[i] += dp[j - 1] * dp[i - j];
        }
    }

    return dp[n];
}