OpenCV基础之常见的图像梯度

梯度是一个向量，梯度方向指向函数变化最快的方向，大小就是它的模，也是最大的变化率。
图像梯度是指在图像中某个位置处沿着某个方向的变化率，通常用于图像边缘检测和特征提取。
dst = cv2.addWeighted(src1, alpha, src2, beta, gamma, dtype=None)一个图像加权函数，可以将两个图像按照一定的权重进行加权叠加。

src1：表示第一个输入的图像；
alpha：表示第一个输入图像的权重系数；
src2：表示第二个输入的图像；
beta：表示第二个输入图像的权重系数；
gamma：表示一个加权值，一般为0；
dtype：表示输出图像的数据类型，一般为np.uint8或np.float32。

dst = cv2.normalize(src, dst=None, alpha=None, beta=None, norm_type=None, dtype=None, mask=None)一个图像归一化函数，可以将图像的像素值缩放到指定范围内。

src：表示输入的图像；
dst：表示输出的图像，如果为None，则输出的图像大小和类型与输入图像相同；
alpha：表示归一化的下界，一般为0；
beta：表示归一化的上界，一般为255；
norm_type：表示归一化的类型，一般为cv2.NORM_MINMAX；
dtype：表示输出图像的数据类型，一般为np.uint8或np.float32；
mask：表示掩膜图像，用于指定哪些像素需要进行归一化。

以下是典型的3*3模板，其模板中心对应要求梯度的原图像坐标(x,y)，（x,y）对应的8邻域的像素灰度值如下表所示：

f(x-1,y+1)	f(x,y+1)	f(x+1,y+1)
f(x-1,y)	f(x,y)	f(x+1,y)
f(x-1,y-1)	f(x,y-1)	f(x+1,y-1)

Roberts交叉算子

Roberts交叉算子其本质是一个对角线方向的梯度算子，不是上面所示的33模板，而是33模板的右上角四个像素点，对应的水平方向和竖直方向的梯度分别为：

x轴梯度模板：[[0,1],[-1,0]]------>G(x) = f(x+1,y+1) - f(x,y)
y轴梯度模板：[[1,0],[0,-1]]------>G(y) = f(x,y+1) - f(x+1,y)

优点：边缘定位较准，适用于边缘明显且噪声较少的图像。

缺点：①没有描述水平和垂直方向的灰度变化，只关注了对角线方向，容易造成遗漏。②鲁棒性差，由于点本身参与了梯度计算，不能有效抑制噪声的干扰。

# 读取图像
img = cv2.imread('img/lena.jpg')
# 转换为灰度图像
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 定义Prewitt算子的卷积核
roberts_x = np.array([[0, 1], [-1, 0]], dtype=np.float32)
roberts_y = np.array([[1, 0], [ 0, 1]], dtype=np.float32)
# 函数cv2.filter2D()来实现卷积操作，可以使用该函数来实现Roberts交叉算子
roberts_img_x = cv2.filter2D(gray, -1, roberts_x)
roberts_img_y = cv2.filter2D(gray, -1, roberts_y)
# 将图像的像素值缩放到指定范围内
roberts_img = cv2.addWeighted(roberts_img_x, 0.5, roberts_img_y, 0.5, 0)
# 显示Roberts交叉算子的梯度图
cv2.imshow('Roberts Gradient', roberts_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

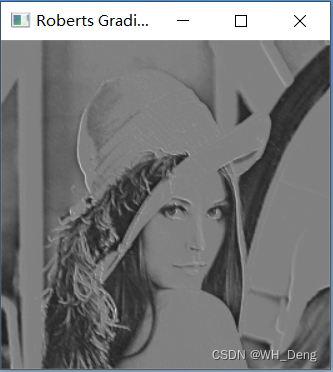
在这里插入图片描述

Prewitt算子

对应的水平方向和竖直方向的梯度分别为：

x轴梯度模板：[[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]]------>G(x) = f(x+1,y+1) - f(x-1,y+1)+f(x+1,y)-f(x-1,y)+f(x+1,y-1)-f(x-1,y-1)
y轴梯度模板：[[ 1, 1, 1], [ 0, 0, 0], [-1, -1, -1]]------>G(y) = f(x-1,y+1) - f(x-1,y-1)+f(x,y+1)-f(x,y+1)+f(x+1,y+1)-f(x+1,y-1)
Prewitt算子引入了类似局部平均的运算，对噪声具有平滑作用，较Roberts算子更能抑制噪声。

# 读取图像
img = cv2.imread('img/lena.jpg')
# 转换为灰度图像
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 定义Prewitt算子的卷积核
prewitt_x = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=np.float32)
prewitt_y = np.array([[ 1, 1, 1], [ 0, 0, 0], [-1, -1, -1]], dtype=np.float32)
# 函数cv2.filter2D()来实现卷积操作，可以使用该函数来实现Prewitt算子
prewitt_img_x = cv2.filter2D(gray, -1, prewitt_x)
prewitt_img_y = cv2.filter2D(gray, -1, prewitt_y)
prewitt_img = cv2.addWeighted(prewitt_img_x, 0.5, prewitt_img_y, 0.5, 0)
# 显示Prewitt算子的梯度图
cv2.imshow('Prewitt Gradient', prewitt_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

在这里插入图片描述

Sobel算子

1.定义两个3*3的卷积核，分别表示水平和垂直方向上的梯度变化

2.将卷积核通过中心点与图像中的像素点进行卷积运算，得到图像中各个像素点在水平和垂直方向上的梯度值：

x轴梯度模板：[[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]------>G(x) = f(x+1,y+1) - f(x-1,y+1) + 2*f(x+1,y) - 2* f(x-1,y)+f(x+1,y-1)-f(x-1,y-1)
y轴梯度模板：[[1, 2, 1], [0, 0, 0], [-1, -2, -1]]------>G(y) = f(x-1,y+1) - f(x-1,y-1) + 2*f(x,y+1) - 2*f(x,y-1)+f(x+1,y+1)-f(x+1,y-1)

dst = cv2.Sobel(src, ddepth, dx, dy, ksize=None, scale=None, delta=None, borderType=None)

src：表示输入的图像；
ddepth：表示输出图像的深度，通常为-1，表示与输入图像的深度相同；
dx：表示在x方向上求导的阶数，一般为0、1或2；
dy：表示在y方向上求导的阶数，一般为0、1或2；
ksize：表示Sobel算子的大小，一般为3、5、7等；
scale：表示缩放因子，一般为1；
delta：表示偏移量，一般为0；
borderType：表示边界处理方式，一般为cv2.BORDER_DEFAULT。

3.梯度大小（也称为梯度幅值）可以使用以下公式计算： |G| = sqrt(Gx^2 + Gy^2)

注：Sobel算子其实就是增加了权重系数的Prewitt算子，且Sobel算子引入了类似局部加权平均的运算，对边缘的定位比Prewitt算子好。

# 读入图像
img = cv2.imread('img/lena.jpg', cv2.IMREAD_GRAYSCALE)
# 使用Sobel算子在x方向上求导
sobelx = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
# 使用Sobel算子在y方向上求导
sobely = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
# 计算每个像素的梯度大小
sobel = np.sqrt(sobelx ** 2 + sobely ** 2)
# 将梯度大小映射到0-255之间，并转换为8位无符号整型
sobel = cv2.normalize(sobel, None, 0, 255, cv2.NORM_MINMAX)
sobel = np.uint8(sobel)
# 显示结果
cv2.imshow('Sobel', sobel)
cv2.waitKey(0)
cv2.destroyAllWindows()

在这里插入图片描述

Laplacian算子

laplacian 是利用二阶导数来检测边缘

卷积核为[[0,1,0],[1,-4,1],[0,1,0]]

dst = cv2.Laplacian(src, ddepth, ksize=None, scale=None, delta=None, borderType=None)

src1：表示输入的图像；
ddepth：表示输出图像的深度，通常为-1，表示与输入图像的深度相同；
ksize：表示Laplacian算子的大小，一般为3、5、7等；
scale：表示缩放因子，一般为1；
delta：表示偏移量，一般为0；
borderType：表示边界处理方式，一般为cv2.BORDER_DEFAULT。

# 读入图像
img = cv2.imread('img/lena.jpg', cv2.IMREAD_GRAYSCALE)
# 使用Laplacian算子计算图像的拉普拉斯值
laplacian = cv2.Laplacian(img, cv2.CV_64F, ksize=3)
# 将梯度大小映射到0-255之间，并转换为8位无符号整型
laplacian = cv2.normalize(laplacian, None, 0, 255, cv2.NORM_MINMAX)
laplacian = np.uint8(laplacian)
# 显示结果
cv2.imshow('Laplacian', laplacian)
cv2.waitKey(0)
cv2.destroyAllWindows()