摘要:
阵列天线的激励幅度和相位控制着其方向图形状。例如锥削分布的幅度可实现低副瓣、递变相位激励可改变波束指向,采用幅相综合控制则可实现平顶波束、余割平方等波束赋形。下面介绍利用Matlab optimtool优化阵列天线的幅相激励实现上述需求。
推文内的完整公式可通过点击公式处并右滑来查看!
均匀平面阵的方向图
前面关于阵列天线方向图综合的推文都是以均匀直线阵为例,本节将介绍均匀平面阵列的方向图综合公式。
下图是矩形网格排列的均匀递变相位的二维平面阵,阵因子S(θ,φ)可表示为:
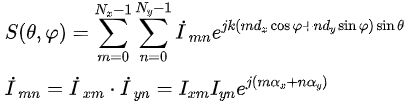
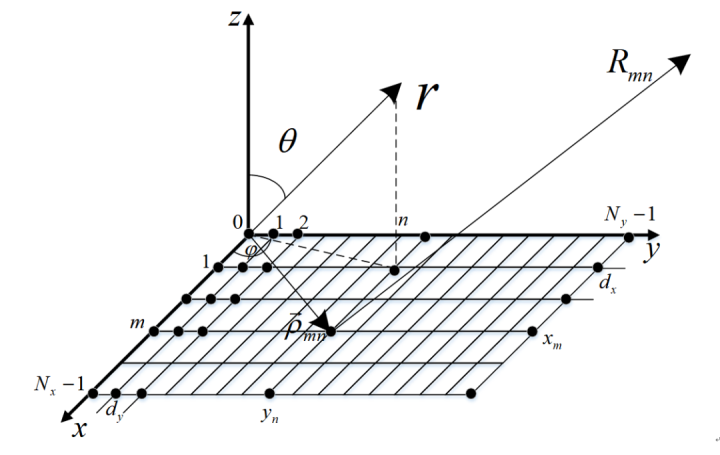
式中,Ixm和Iym分别为沿和方向排列的直线阵的激励幅度;ax和ay分别是沿x和y方向排列的直线阵的均匀递变相位,
利用分离变量法可将上述二维均匀平面阵阵因子简化为[1]:

考虑大地板的存在,为简化计算,求解区域仅考虑:
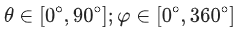
为了在直角坐标系中绘出极坐标三维图形效果,考虑把布阵平面由xy平面转换为yz平面。即,将u-v进行如下变换操作:

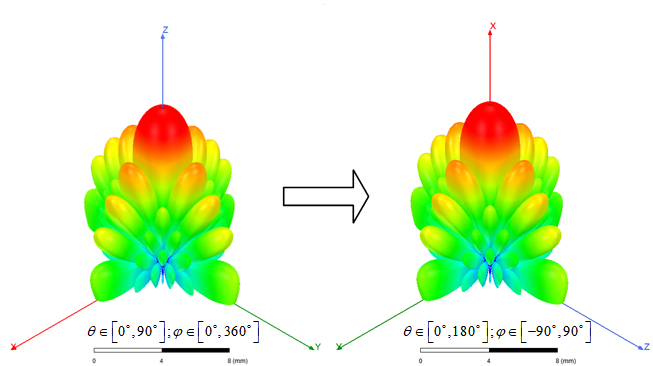
对单元间距为0.5个工作波长的8×8方形栅格均匀平面阵进行等幅同相激励,利用Matlab即可绘制出其归一化的3D方向图(下文均采用归一化的刻度):
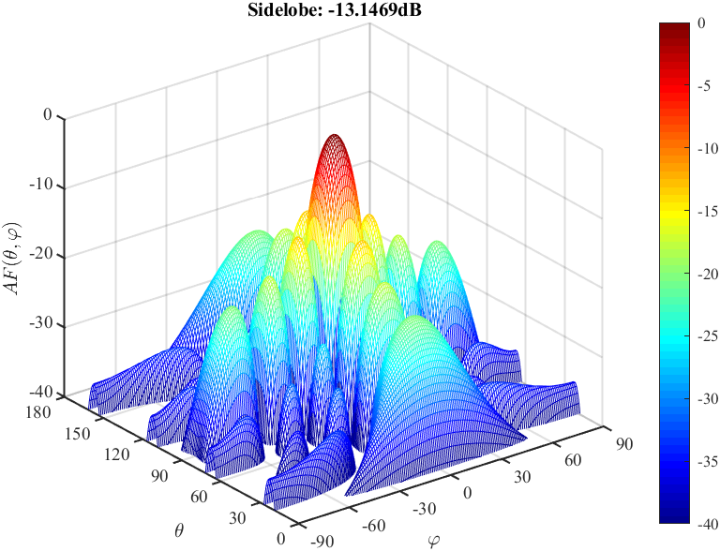
参考资料
[1]R. S. Elliott, Antenna Theory and Design, revised ed.: https://www.wiley.com/en-cn/Antenna+Theory+%26+Design%2C+Revised+Edition-p-9780471449966
低副瓣的优化
在低副瓣阵列的设计原理一文中简单介绍了低副瓣阵列的综合原理和实例。这里采用matlab的optimtool对上一节阵列单元的幅度进行优化(同相激励,单元之间无相差),从而实现低副瓣效果。
根据计算出的3D方向图数据,提取出关键评估参量-第一副瓣的值SLL(dB)。若目标副瓣电平在SLL0(dB)以下,适应度函数可采用最简单的线性评估公式,

之所以加绝对值是考虑到增益不能牺牲太多,因此不需追求极致低副瓣,SLL达到目标值即认定为最优结果。编写好相关matlab代码,在command window界面输入optimtool将其打开,选择GA优化算法并填写好相关数据后,即可进行迭代优化。
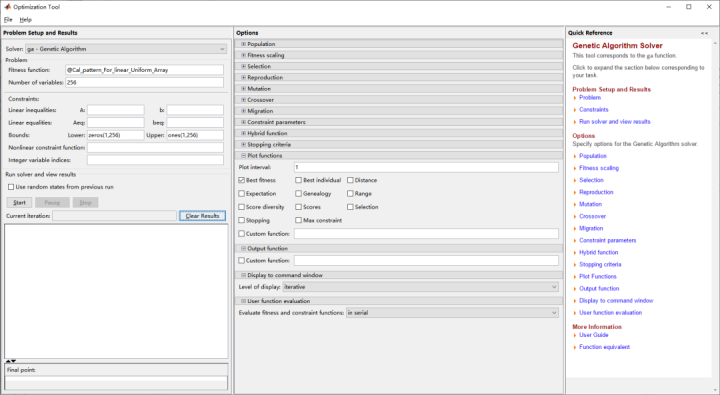
将种群数量和迭代次数分别设置为50和50后,优化结果如下所示:

可以看出,优化的幅度激励虽然显得很杂乱无章,但其第一副瓣电平的值满足指标需求。


波束指向的优化
对于第一小节的均匀平面阵,可用理论公式计算任意俯仰、方位角度波束扫描对应的相位分布。在优化前需要将第一小节的公式做出如下改变:

本小节则利用matlab的optimtool对该等幅激励的平面阵列的单元馈电相位进行优化,实现任意角度的波束指向。需要注意的是,适应度函数需要同时考虑最大波束指向和副瓣电平值:
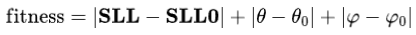
上述三项可根据优先级进行系数加权,这里采用最简单的平均分配。设立需求目标如下:
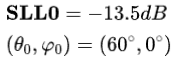
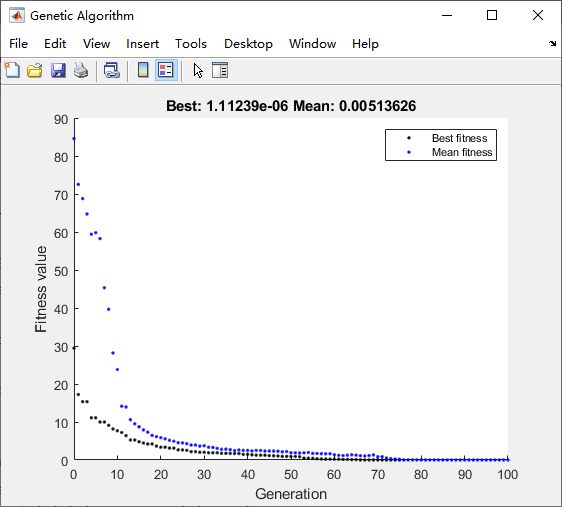
从下图可以看出,本次优化过程达到收敛的迭代次数比第二节的多,50代后才逐渐得到收敛。仿真数据表明,最终的优化完全满足指标的波束指向和副瓣要求。当然,增益下降问题可以通过在适应度函数里添加有关天线增益的一项,并给予合适的权重来解决。

平顶波束赋形的优化
阵列天线的赋形波束综合(一),阵列天线的赋形波束综合(二)这两篇推文以一个直线阵为例,分别用傅里叶级数法和伍德沃德—劳森抽样法实现了方形波束。本小节则通过GA算法优化单元的激励幅度和相位来实现3维的平顶波束。假设平顶波束满足下述条件:

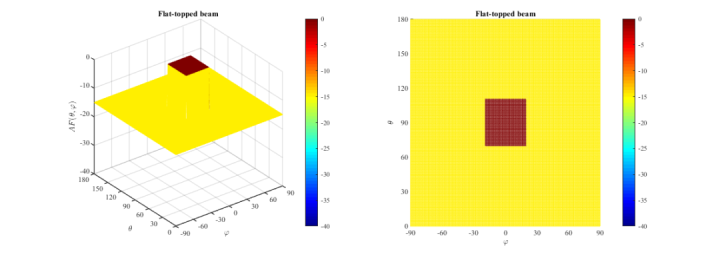
利用对称性可以将优化变量由128个缩减至32个,同时需要调整适应度函数。其关键点在对平顶波束区域均值和非平顶波束区域最大电平值分配不同的权重(前者权重过大容易获得高副瓣结果,后者权重过大则容易恶化平顶波束区域的平坦度)。
选用如下适应度函数,采取种群个数100,最大迭代次数200。

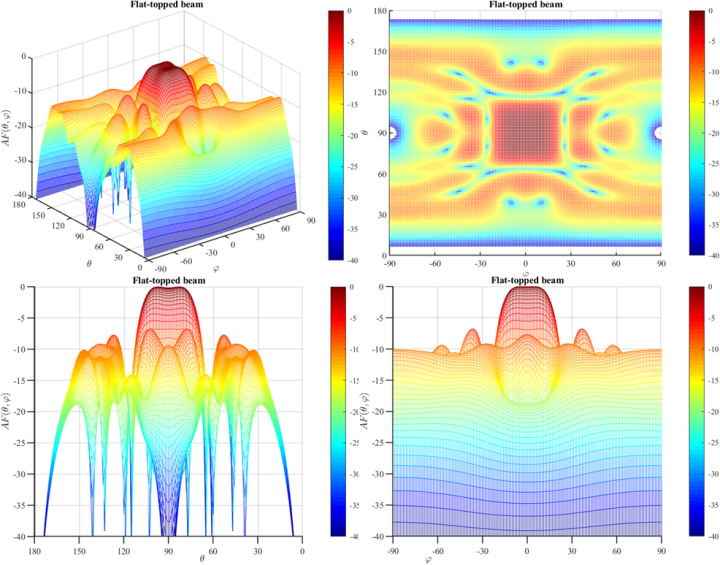
从下面的仿真数据可以看出:适应度函数并没有收敛到理想值,这与设定的目标条件是否苛刻,理论上是否能达到目标值以及算法的局限性都有关系。最优结果显示,平顶区域基本成型且该区域的纹波较小,但其他区域的副瓣电平值相对较高。
由于本次优化目标的方向图为理想的平顶波束,平顶区域内的平坦度和边界区域下的跳变特性都过于理想。更好的优化结果则可通过构造可实现性更强的目标方向图,并适当调整适应度函数等改进措施来得到。

-END-
作者:微波天线工程师
来源:Matlab optimtool优化阵列天线的幅相激励
关于RFASK射频问问
射频问问是在"微波射频网”系列原创技术专栏基础上升级打造的技术问答学习平台,主要围绕射频芯片、微波电路、天线、雷达、卫星等相关技术领域,致力于为无线通信、微波射频、天线、雷达等行业的工程师,提供优质、原创的技术问答、专栏文章、射频课程等学习内容。更多请访问:RFASK射频问问 - 射频技术研发服务平台 | 技术问答、专栏文章、射频课程