二叉树

🌳1.树的概念
🌳2.二叉树的概念及性质
- 🍎2.1 二叉树的概念
- 🍎2.2 二叉树的性质
🌳3.二叉树的基本操作
- 🍎3.1 二叉树的遍历
- 🍎3.2 获取树中节点的个数
- 🍎3.3 获取叶子节点的个数
- 🍎3.4 获取第K层节点的个数
- 🍎3.5 获取二叉树的高度
- 🍎3.6 检查值为value的元素是否存在
- 🍎3.7 层次遍历
- 🍎3.8 判断二叉树是不是完全二叉树

在学习二叉树之前，我们有必要了解一下树的概念和常用术语。接下来以下面这棵树为例来回顾下树相关概念：
在这里插入图片描述

🌳1.树的概念

树的概念：一种非线性的数据结构，由n(n >=0)个节点组成的一个具有层次关系的集合。树的术语：

节点的度一个节点含有子树的个数，例如上图中A的度为6.
树的度树上所有节点的度的最大值，例如上图中树的度为6.
叶子结点度为0的节点，例如上图中的K、L、M…
根节点树中没有双亲节点的节点。例如，上图中树的根节点为A。、
子节点一个节点含有的子树的根，如上如，B是A的子节点
父节点一个节点有子节点，则称这个节点为其子节点的父节点。如上图A时B的父节点

🌳2.二叉树的概念及性质

🍎2.1 二叉树的概念

二叉树是树的一种特殊形式，空树是二叉树，或者树中所有节点的度小于二的树称为二叉树。如下图所示，接下来介绍二叉树我们以这张图片上的树形为准：

在这里插入图片描述

🍎2.2 二叉树的性质

规定根节点的层次为1，则一颗非空二叉树的第 i 层上最多有：2^k-1个节点
规定根节点的二叉树深度为1，则深度为k的那层的二叉树的最大节点数为：2^k-1（k>=0）
对于任何一颗二叉树 ,如果器叶子节点数为n₀，度为2的节点数为n₂，则有n₀ = n₂ + 1
具有 n 个节点的完全二叉树的深度k 为：log₂(n+1) 向上取整.

🌳3.二叉树的基本操作

🍎3.1 二叉树的遍历

🌳前序遍历
前序遍历的二叉树将按照先访问根节点，再访问左子树，最后访问右子树的过程递归进行，最终遍历结束所有的节点。
前序遍历的过程如下：

public void preOrder(TreeNode root) {
	if(root != null) {
		System.out.print(root.val+" ");
		preOrder(root.left);
		preOrder(root.right);		
	}	
}

按照前序遍历结果，则上述二叉树的遍历结果为：A->B->D->E->H->C->F->G

🌳中序遍历
中序遍历的二叉树将按照先访问左子树，再访问根节点，最后访问右子树的过程递归进行，最终遍历结束所有的节点。
中序遍历的过程如下：
public void inOrder(TreeNode root) {
    if (root != null) {
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    } }
根据上图的遍历过程，我们可以得到上述二叉树的中序遍历结果为：D->B->E->H->A->F->C->G

🌳后序遍历
后序遍历的二叉树将按照先访问左子树，再访问右子树，最后访问根节点的过程递归进行，最终遍历结束所有的节点。
后续遍历的过程如下：
    public void postOrder(TreeNode root) {
        if (root != null) {
            postOrder(root.left);
            postOrder(root.right);
            System.out.print(root.val + " ");
        }
    }
由上图后续遍历过程可知，图中二叉树的遍历结果为：D->H->E->B->F->G->C->A

🌳层次遍历
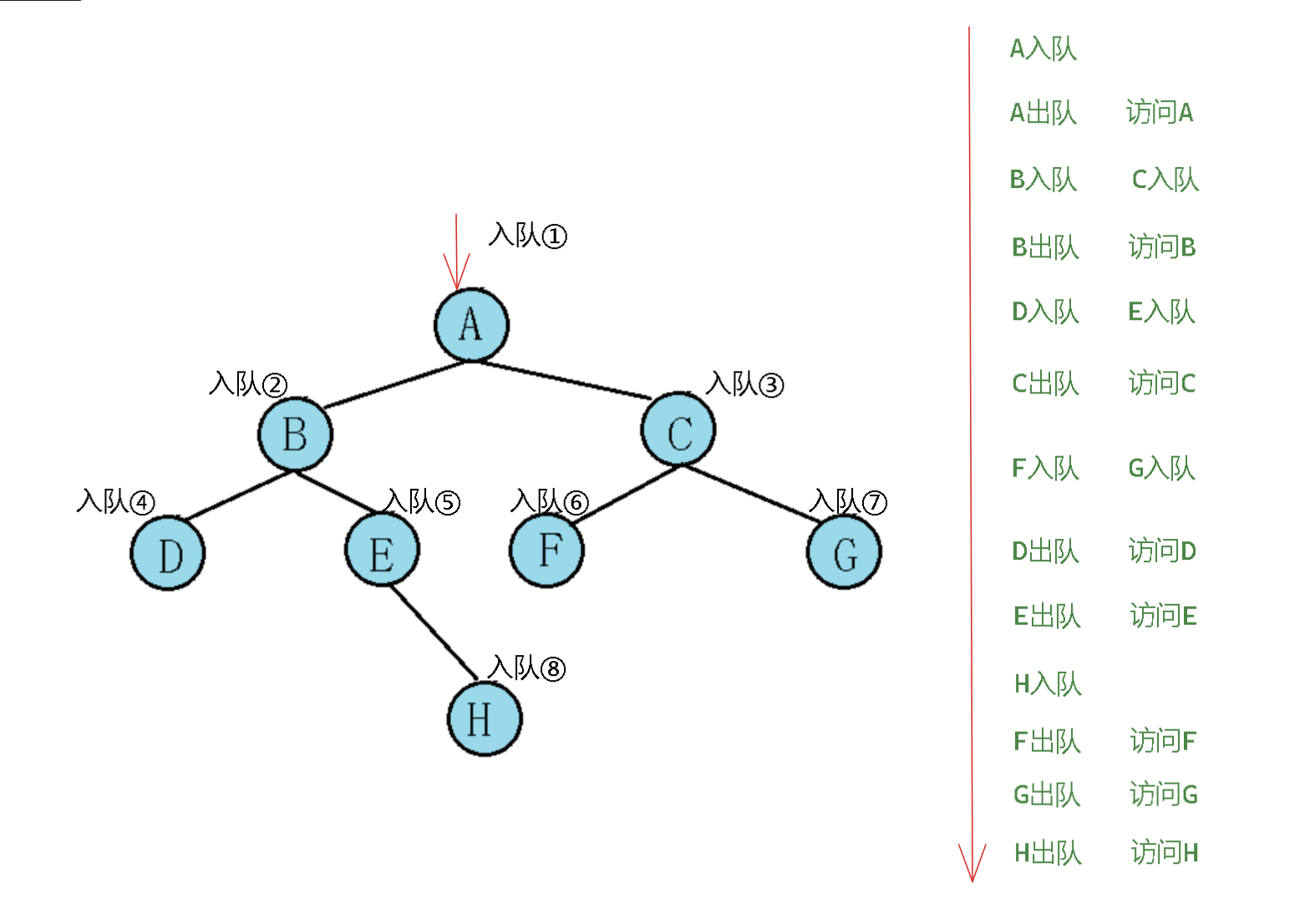
二叉树的层次遍历即按照二叉树的层次顺序从左到右遍历节点，过程如下图所示：

因为二叉树的遍历无法直接按照遍历顺序进行层次节点的访问，因此我们需要借助队列的这种数据结构来实现二叉树的层次遍历。层次遍历的原理即上述二叉树的详细入出队列过程如下：

    public void levelOrder(TreeNode root) {
        ArrayDeque<TreeNode> charQueue = new ArrayDeque<>();  //创建一个队列
        charQueue.offer(root);  //将根节点入队列
        while(!charQueue.isEmpty()) {
            TreeNode pollNode = charQueue.poll();	//只要队列不为空，就从队列中取出节点访问
            System.out.print(pollNode.val + " ");
            if(pollNode.left != null) {	
                charQueue.offer(pollNode.left);
            }
            if(pollNode.right != null) {
                charQueue.offer(pollNode.right);
            }
        }
    }

🍎3.2 获取树中节点的个数

我们可以通过定义计数器以及任何一种遍历方式，拿到二叉树的节点个数，这种方法很简单，那么有没有什么别的方法可以不用定义计数器就获取到节点的个数呢？
不妨这样去向，从根节点开始，这颗二叉树的节点个数等于左子树+右子树+根节点；而对于左子树来说，左子树的节点个数同样等于它的左子树＋有稀疏+根节点的个数。既然这样，我们能否通过直接返回节点个数的方法直接求出总的节点数呢》显而易见，按照上面的方法定义递归算法，可以很容易实现这件事情：
    public int countNode(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftCount = countNode(root.left);
        int rightCount = countNode(root.right);
        return leftCount + rightCount + 1;
    }
这种求节点个数的原理如下图所示：

🍎3.3 获取叶子节点的个数

与上边求节点的个数类似，我们让当前根节点判断是否有左右子树即可。
原理与上边统计节点个数的原理相同，这里就不画图了。

    public int getLeafNodeCount(TreeNode root) {
        if(root == null) {
            return 0;
        }
        if(root.left == null && root.right == null) {
            return 1;
        }
        int leftLeafCount = getLeafNodeCount(root.left);
        int rightLeafCount = getLeafNodeCount(root.right);
        return leftLeafCount + rightLeafCount;
    }

🍎3.4 获取第K层节点的个数

若规定二叉树根节点的层次为1，则对根节点层次来说，求得是其第k层的节点个数；对第二层次来说求的是其第k-1层的节点个数…，那么，我们使用递归算法，当k的相对值变为1时，则返回1代表第k层上节点的个数，将左右子树的值相加返回即可.
/**
 * 求二叉树第k层上的节点的个数  
 * @param root  二叉树的根节点  
 * @param k 求解的层数  
 * @return 返回节点个数  
 */
  public int getLevelNodeCount(TreeNode root, int k) {
    if (root == null) {
        return 0;
    }
    if (k == 1) {
        return 1;
    }
    int leftCount = getLevelNodeCount(root.left, k - 1);
    int rightCount = getLevelNodeCount(root.right, k - 1);
    return leftCount + rightCount; }
这个求解过程如下图所示：

🍎3.5 获取二叉树的高度

某棵二叉树的高度等于它的左子树高度的和右子树高度的最大值加上自己，即高度height = leftTree + rightTree + 1。这仍然是典型的递归算法。当左子树或者右子树为null时，说明二叉树的这一层已经没有节点了，那么返回给上一层递归结果0即可。这个递归算法的程序设计如下：
/**
 * 获取二叉树的高度  *  
 * @param root 二叉树的根节点 
 * @return 返回二叉树的高度 
 */ 
 public int getHeight(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftTreeHeight = getHeight(root.left);
    int rightTreeHeight = getHeight(root.right);
    return Math.max(leftTreeHeight, rightTreeHeight) + 1; 
 }
这个递归过程如下图所示：

🍎3.6 检查值为value的元素是否存在

遍历二叉树的所有节点，如果存在值为value的节点，则返回这个节点，否则返回null。检查的过程为，检查根节点的值是否为value；检查左子树中是否存在；检查右子树中是否存在。递归算法的程序设计如下：

/**
 * 查找二叉树中是否存在值为value的节点
 *  
 * @param value 待查找的值  
 * @return 返回查找结果  
 */
 public TreeNode getValNode(TreeNode root, char value) {
    //如果遍历到最底层还没有找到，返回null
    if (root == null) {
        return null;
    }
    if(root.val == value) {
        return root;
    }
    //从左子树中查找
    TreeNode valNodeInL = getValNode(root.left, value);
    if(valNodeInL != null) {
        return valNodeInL;
    }
    //从右子树中查找
    TreeNode valNodeInR = getValNode(root.right, value);
    if(valNodeInR != null) {
        return valNodeInR;
    }
    return null; 
   }

这个算法的递归过程与先序遍历的过程类似。可以看上边先序遍历的图。

🍎3.7 层次遍历

所谓层析遍历，就是指将二叉树从左到右从上到下依次遍历。为了实现这种遍历效果，我们需要使用队列这种数据结构将当前节点的左右子树根节点依次入栈并在出栈式再依次将出战节点的左右子树根节点入栈，依次进行下去，直到当前栈为空。该算法的程序设计如下：
public void levelOrder(TreeNode root) {
    if(root == null) {
        return;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while(!queue.isEmpty()) {
        TreeNode poll = queue.poll();
        System.out.print(poll.val + " ");
        if(poll.left != null) {
            queue.offer(poll.left);
        }
        if(poll.right != null) {
            queue.offer(poll.right);
        }
    } 
}
该算法的运行过程如下：

🍎3.8 判断二叉树是不是完全二叉树

我们将该二叉树的依次按照层次遍历的顺序入队列（包含最后一层的左右空子树），在出队列时进行判断，如果出队列的节点为null，就停止入队列，并检查队列中剩余节点是否还有非空节点，如果有非空节点，说明这不是一个完全二叉树。例如，下面的这几种二叉树都不是完全二叉树，均满足上述的判定方法：
在这里插入图片描述

public boolean isCompleteTree(TreeNode root) {
    if (root == null) {
        return false;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode poll = queue.poll();   //如果在出队列时遇到null，则停止入队列
        if (poll != null) {
            queue.offer(poll.left);
            queue.offer(poll.right);
        } else {
            break;
        }
    }
    while (!queue.isEmpty()) {
        if (queue.poll() != null) { //如果队列中剩余节点还有非空的，就说明这不是一颗完全二叉树
            return false;
        }
    }
    return true;
 }