类型:数值运算
描述
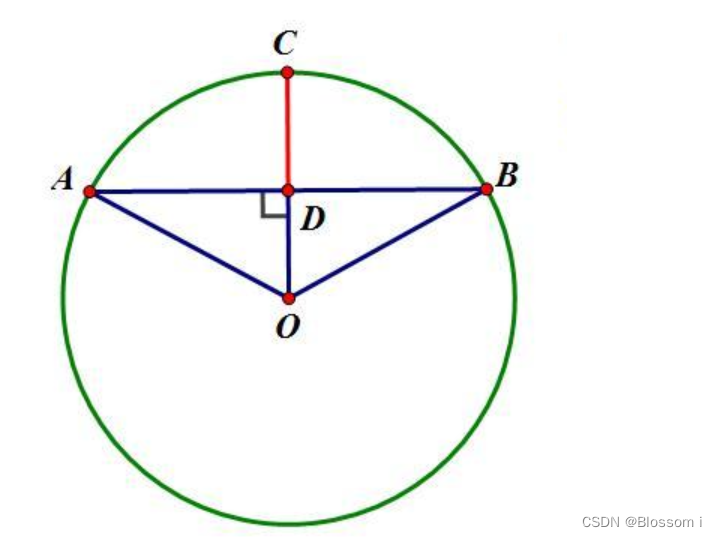
如下图,AB 是圆的一条弦,ABC形成一个弓形,在两行中分别输入弦长AB和弓高CD的长度,计算并分两行依次输出该圆的半径和弓形ABC的面积,结果均严格保留小数点后2位有效数字,应用三角函数和反三角函数时查阅math模块文档或利用自动补全完成。
提示:
从图中可知:
AD = AB / 2 OA2 = AD2 + OD2 OD = OC – CD = OA – CD
代入后可得
OA = (AD2 + CD2 ) / (2 * CD) sin(∠AOB / 2) = AD / OA
圆心角:
∠AOB = 2 * arcsin(AD / OA)
扇形AOB的面积为:
area_of_sector = ∠AOB / (2π) * π *OA2
三角形 △AOB
area_of_triangle = 1 / 2 * OA2 * sin(∠AOB)
弓形面积为扇形AOB面积减去三角形△AOB面积之差:
area_of_arch = area_of_sector - area_of_triangle
输入
分2行输入2个浮点数
输出
在两行内分别输出半径和弓形面积
示例
输入:
26.5
8
输出:
14.97
151.16代码:
import math
# 输入弦长度,浮点数#
#=======================================================
# 补充你的代码
AB=eval(input())
# 输入弓高度,浮点数#
CD=eval(input())
# 计算半弦长#
AD=AB/2
# 计算半径#
OA=(AD**2+CD**2)/(2*CD)
# 计算圆心角#
#=======================================================
AOB=2*math.asin(AD/OA)
# 计算弓形所在扇形的面积#
#=======================================================
area_of_sector = AOB/(2*math.pi)*math.pi*OA**2
# 计算三角形面积#
#=======================================================
area_of_triangle = 1 / 2 *OA**2*math.sin(AOB)
# 计算弓形面积#
#=======================================================
area_of_arch = area_of_sector - area_of_triangle
# 在两行中分别输出半径和弓形面积#
#=======================================================
print(f"{OA:.2f}")
print(f"{area_of_arch:.2f}")