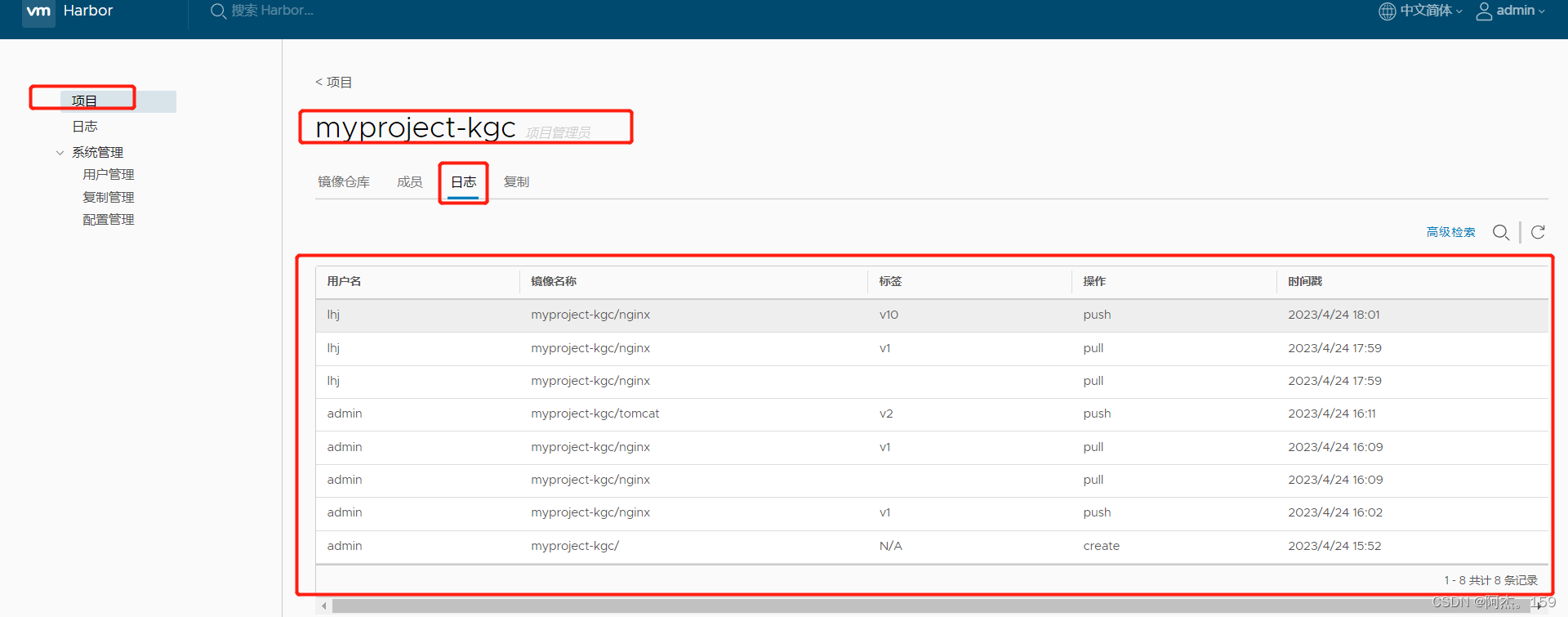
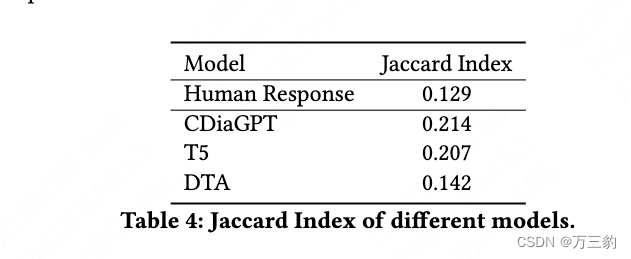
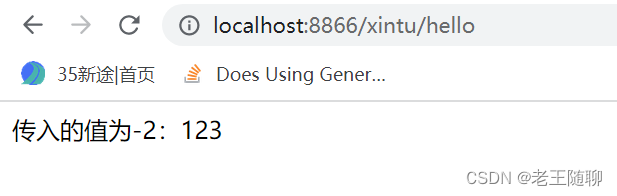
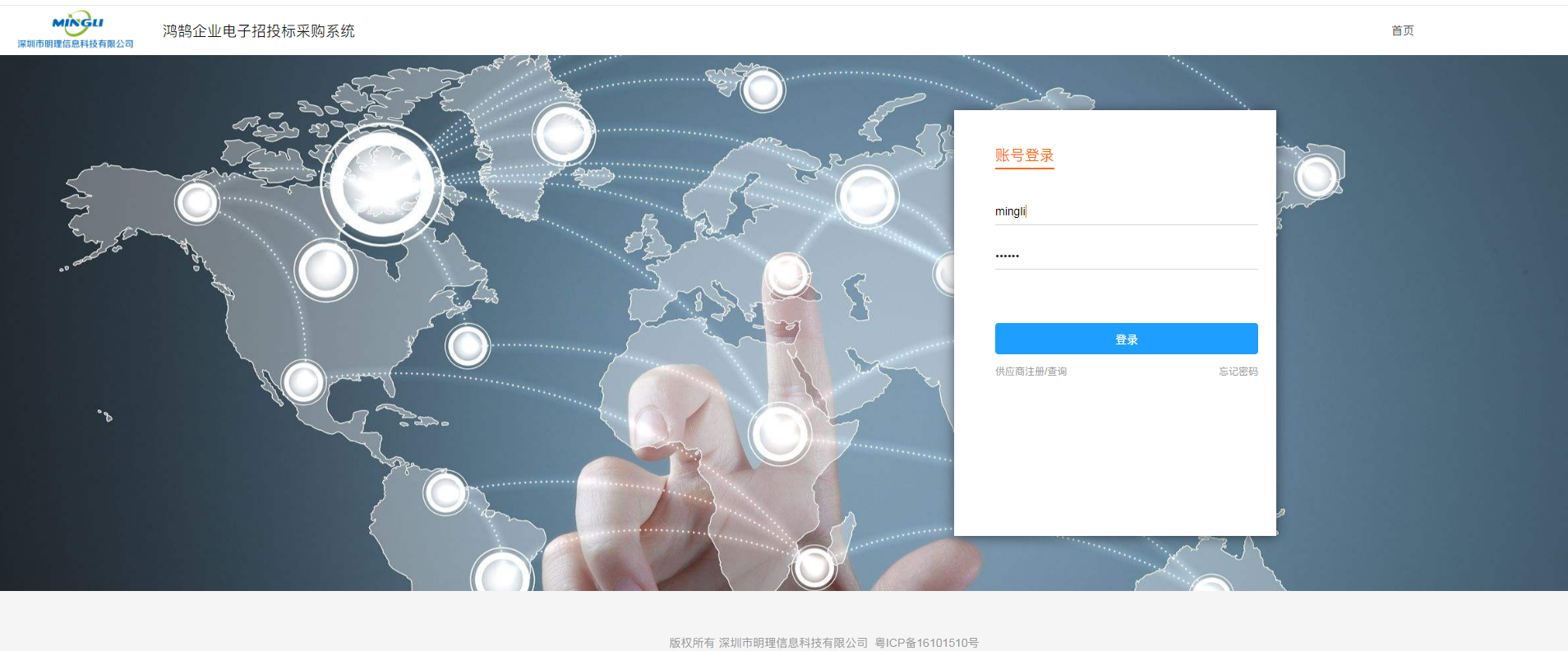
学习目标：

当学习行列式性质和计算时，以下是一些具体的学习目标：

1. 理解行列式的定义和计算方法，能够准确计算给定的行列式。（最基本的）
2. 熟练掌握行列式的基本性质，包括交换行列式的两行或两列、用一个数乘行列式的某一行或某一列、将两行或两列相加到另一行或另一列上等。
3. 熟练运用性质计算行列式，能够灵活地应用不同的性质来简化行列式的计算。
4. 了解行列式的一些基本定理，如Cramer定理和Laplace定理，并了解如何运用这些定理解决实际问题。
5. 能够应用行列式来解决线性方程组的求解问题，以及矩阵的求逆问题。
6. 理解行列式的几何意义，能够将行列式与几何图形相联系，例如用行列式计算三角形的面积和四面体的体积。
7. 进一步拓展行列式的应用，如在微积分、偏微分方程和量子力学等领域中的应用。

以上是学习行列式性质和计算的一些具体的学习目标，学生可以根据自己的实际情况和学习进度进行调整和补充。

 我的学习步骤：

我要学习行列式的性质和计算，我可能会采取以下步骤：

1. 学习行列式的定义：首先，我会学习行列式的定义和计算方法，包括三阶和更高阶矩阵的行列式计算方法。我会确保自己对行列式的定义和计算方法有清晰的理解。

2. 学习行列式的性质：接下来，我会学习行列式的性质，包括交换行列式的两行或两列、用一个数乘行列式的某一行或某一列、将两行或两列相加到另一行或另一列上等。我会通过实例演示和证明来加深对这些性质的理解。

3. 练习行列式的计算：然后，我会练习行列式的计算，通过计算各种规模和类型的矩阵的行列式来加深对行列式计算的熟练程度。我会尝试使用不同的计算方法，包括逐步展开、使用初等变换等。

4. 应用行列式：最后，我会探索行列式在实际应用中的作用，包括线性方程组的求解、矩阵的求逆和行列式的几何意义等。我会通过实际应用来加深对行列式的理解和应用能力。

在学习过程中，我还会查阅数学书籍、网上资源和寻求他人的帮助，以获得更全面和深入的学习经验。我会持续练习和实践，以提高自己的数学技能和应用能力。

 1.2.1 行列式的性质————我的理解

行列式的性质1指出，将矩阵的任意两行（或任意两列）互换，行列式的值不变。该性质也被称为行列式的行列互换性。

这个性质可以用数学语言描述为：设$A$为$n$阶矩阵，交换$A$的第$i$行和第$j$行（或第$i$列和第$j$列）后得到的矩阵为$A'$，则有$\det(A)=\det(A')$。

可以通过计算例子来验证这个性质。例如，设$A=\begin{bmatrix}1 & 2 \3 & 4 \end{bmatrix}$，交换矩阵$A$的第1行和第2行，得到的矩阵为$A'=\begin{bmatrix}3 & 4 \1 & 2 \end{bmatrix}$，则有：

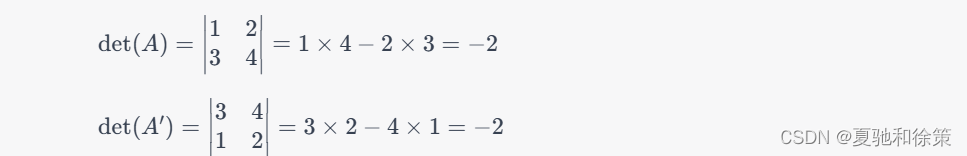
可以看到，交换矩阵$A$的第1行和第2行后，矩阵$A$的行列式值与原来的值相同。

 性质1.1 怎么用

行列式的性质1有着广泛的应用，以下是一些例子：

1. 矩阵求逆：通过对矩阵进行初等行变换（包括交换行列、乘以非零数、加上另一行的若干倍）可以将矩阵变为一个上三角矩阵，从而可以求出其行列式，进而求出矩阵的逆。在交换行列的过程中，行列式的值不变，因此逆矩阵的行列式也相同。

2. 计算多项式系数：例如，多项式$(x_1+x_2+x_3)^3$中$x_1^2x_3$的系数可以通过矩阵求行列式来计算。具体来说，构造一个由$x_1,x_2,x_3$的所有二元组组成的$3\times 3$矩阵，将其中的$x_1^2x_3$换到第一列，然后计算矩阵的行列式，即可得到$x_1^2x_3$的系数。

3. 判断矩阵的线性相关性：若一个$n$阶矩阵的行向量（或列向量）线性相关，则矩阵的行列式为0。这是因为，若一个矩阵的行向量线性相关，则它们可以通过一些线性组合得到零向量，而零向量的行列式为0。

总之，行列式的性质1为矩阵论和线性代数提供了一种有效的工具和方法，可以应用于求逆矩阵、计算多项式系数、判断线性相关性等问题。

性质1.2 

行列式的性质2指出，如果将矩阵的某一行（或某一列）乘以一个数$k$，那么该数可以提取到行列式的外面。具体来说，如果将矩阵$A$的第$i$行（或第$j$列）乘以$k$，得到的矩阵为$A'$，则有$\det(A')=k\det(A)$。

这个性质可以用数学语言描述为：设$A$为$n$阶矩阵，将$A$的第$i$行乘以$k$（或将$A$的第$j$列乘以$k$）得到的矩阵为$A'$，则有$\det(A')=k\det(A)$。

我们可以通过一个例子来验证这个性质。例如，设$A=\begin{bmatrix}1 & 2 \3 & 4 \end{bmatrix}$，将矩阵$A$的第1行乘以2，得到的矩阵为$A'=\begin{bmatrix}2 & 4 \3 & 4 \end{bmatrix}$，则有：

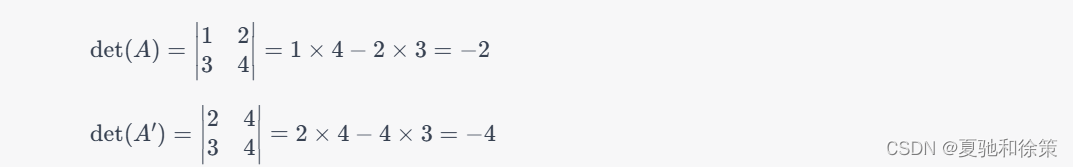
可以看到，将矩阵$A$的第1行乘以2后，矩阵$A$的行列式值乘以2，即$\det(A')=2\det(A)$。

行列式的性质2有着广泛的应用，例如，可以通过这个性质将矩阵变为行最简形式，进而求解线性方程组，也可以用于计算高斯积分等问题。

性质2 怎么用 

行列式的性质2可以用于简化行列式的计算过程。具体来说，如果矩阵$A$的某一行（或某一列）可以被一个公因子$k$整除，那么可以将该行（或列）除以$k$，然后再将$k$提取到行列式的外面，从而得到一个更简单的行列式。

举一个简单的例子，考虑计算矩阵$A=\begin{bmatrix}2&4\\3&6\end{bmatrix}$的行列式。可以发现，第2行可以被2整除，因此可以将第2行除以2，然后将2提取到行列式的外面，得到：

$$\begin{vmatrix}2&4\\3&6\end{vmatrix}=2\begin{vmatrix}1&2\\3&6\end{vmatrix}=2\begin{vmatrix}1&2\\0&0\end{vmatrix}=0$$

在这个例子中，使用了行列式的性质2将第2行除以2，并将2提取到行列式的外面，从而得到了一个更简单的行列式。

行列式的性质2也可以用于求解线性方程组。具体来说，如果线性方程组的系数矩阵的某一行（或某一列）可以被一个公因子$k$整除，那么可以将该行（或列）除以$k$，然后再将$k$提取到行列式的外面，得到一个更简单的系数矩阵。这样就可以使用高斯消元法等方法求解线性方程组。

性质1.3 

行列式的性质1.3是指，如果行列式的两行（或两列）成比例，即其中一行（或一列）等于另一行（或一列）乘以一个常数$k$，那么行列式的值为0。

具体来说，如果矩阵$A$的第$i$行等于第$j$行乘以一个常数$k$，即$A_{i1}=kA_{j1}, A_{i2}=kA_{j2},\ldots,A_{in}=kA_{jn}$，那么该行列式的值为0，即$\det(A)=0$。

这个性质的证明可以通过展开行列式来得到。展开行列式时，可以选择两行（或两列）进行展开。如果其中有两行（或两列）成比例，那么展开后的结果中会出现两个相同的子式，这两个子式的乘积为0，因此整个行列式的值为0。

这个性质的应用场景比较多，例如在求解线性方程组的过程中，可以通过交换方程的顺序，将系数矩阵变为一个上三角矩阵或下三角矩阵，然后再使用行列式的性质1.3将矩阵化为行最简形式，从而得到方程组的解。此外，在线性代数、微积分等领域的很多理论证明中，也会使用到这个性质。

 

 性质1.4 

行列式的性质4指出，如果一个行列式的两行（或两列）交换，则该行列式的值会改变符号。

具体来说，设行列式为$A$，其中第$i$行和第$j$行交换，得到行列式$B$，则有：

 

其中$B_{ij}$表示行列式$B$的第$i$行，第$j$列的元素，$A_{ij}$表示行列式$A$的第$i$行，第$j$列的元素。

同样地，如果是交换了两列，则结果也是一样的，行列式的值会改变符号。这个性质也可以推广到交换多行或多列的情况，交换偶数行或列时行列式的值不变，交换奇数行或列时行列式的值改变符号。

性质4的证明可以通过将行列式展开为代数余子式的形式来进行推导。由于代数余子式中有$i$行$j$列的元素，因此当第$i$行和第$j$行交换时，每个代数余子式都会变号，从而导致整个行列式的值也会改变符号。

 性质1.5

行列式的性质1.5指出，如果将一个行列式的某一行（或列）的倍数加到另一行（或列）上，得到的新行列式与原行列式具有相同的值。

具体来说，设行列式为$A$，将$A$的第$i$行的$k$倍加到$A$的第$j$行上得到新的行列式$B$，则有：

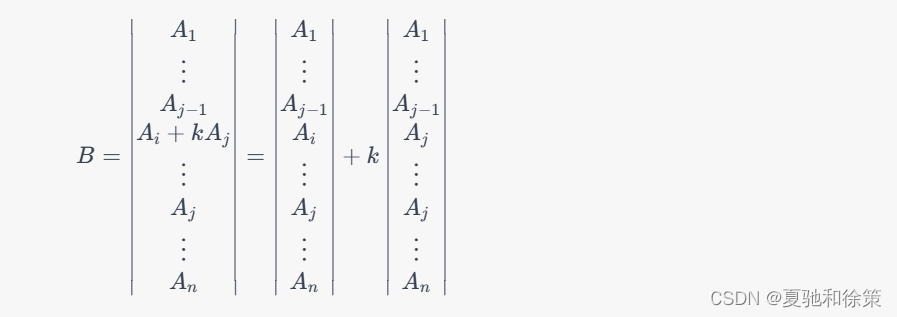
上式中，第一个行列式等于原行列式$A$，第二个行列式中有两行相同，因此等于零，即$B=A$。

同样地，如果是将某一列的倍数加到另一列上，也可以得到相同的结论。

这个性质可以通过对行列式进行初等变换来推导得到。因为初等变换不改变行列式的值，所以将一个行的倍数加到另一个行上后，行列式的值也不会改变。

 性质1.6

1.2.2 我的理解：

行列式的展开式是计算行列式的一种方法，可以将$n$阶行列式的计算转化为$n-1$阶行列式的计算。

对于$n$阶行列式$A$，我们可以选择其中一行（或一列），以此为基础将该行（或列）展开成$n$个代数余子式（或代数余子式的相反数）的和，即：

 

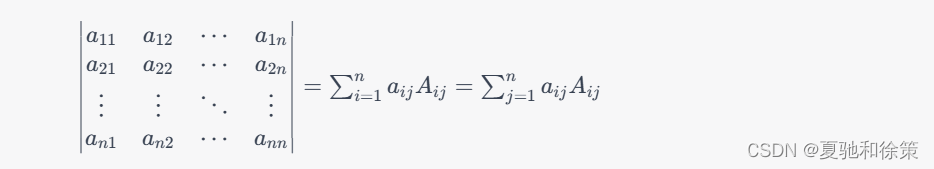
其中，$A_{ij}$表示$a_{ij}$的代数余子式。

具体来说，我们可以选择第一行进行展开，得到：

 

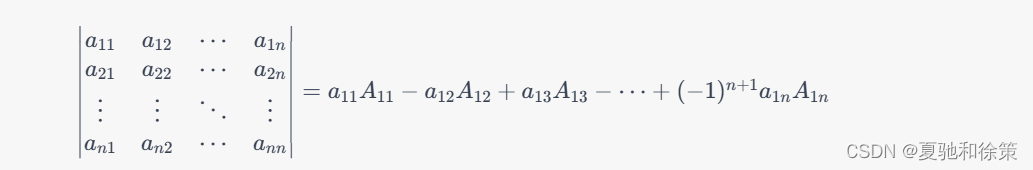
这样，我们就将$n$阶行列式转化为了$n-1$阶行列式的计算，而$n-1$阶行列式的计算可以继续使用这个方法展开，直到变成$2$阶行列式，此时可以直接计算。

需要注意的是，展开的某一行（或列）的选择不是唯一的，不同的选择可能得到不同的展开式，但它们的值是相等的。

 

 具体解释：

好的，让我们以一个$3$阶行列式为例来具体解释一下展开式的使用方法。

假设我们要计算下面这个$3$阶行列式$A$：

 

我们可以选择第一行展开，得到：

 

我们发现，展开后得到的是$2$阶行列式的形式，我们可以继续使用相同的方法，选择某一行或列展开，直到得到$2$阶行列式，然后可以直接计算。

比如，我们继续选择第一行展开第一个$2$阶行列式，得到：

 

同理，我们可以得到另外两个$2$阶行列式的值：

将它们代入展开式中，得到：

 

因此，我们得到了该$3$阶行列式的值为$0$。

这就是使用展开式计算行列式的方法，通过选择某一行或列进行展开，可以将$n$阶行列式转化为$(n-1)$阶行列式的计算，直到最终得到$2$阶行列式，可以直接计算出其值。需要注意的是，不同的行或列选择可能会得到不同的展开式，但它们的值是相等的。

行列式的计算可以通过以下步骤完成：

1. 根据展开定理选择一行或一列进行展开。

2. 对选择的行或列的每个元素，乘以其对应的代数余子式（即去掉该行和该列后形成的矩阵的行列式）。

3. 将上述乘积相加，得到最终的行列式的值。

例如，对于一个3阶行列式：

 

可以选择第一行展开：

 

然后，可以计算每个代数余子式：

 

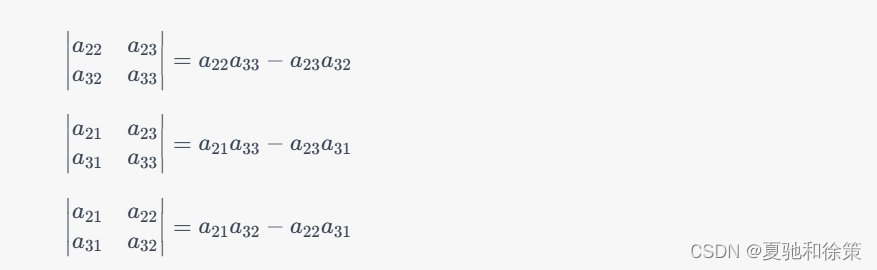
将它们代入展开式中，得到：

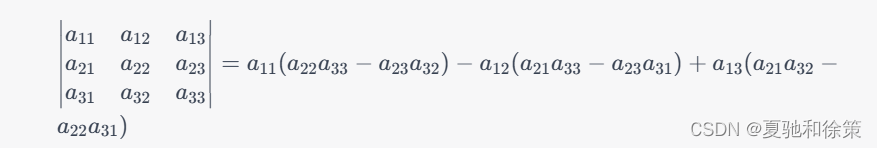
将各项乘积相加，即可得到行列式的值。

总结：

行列式是线性代数中的重要概念之一，其重点、难点和易错点如下：

重点：

• 行列式的概念及其性质，包括行列式的计算方法、性质及推论；
• 行列式的应用，例如线性方程组求解、矩阵求逆等。

难点：

• 行列式的计算过程，需要注意化简方法、判断行列式是否可逆等问题；
• 行列式的应用中，对于不同问题需要根据实际情况灵活选择合适的行列式性质或方法进行求解。

易错点：

• 行列式计算过程中的代数计算错误，如错误地提公因子、错误地展开行列式等；
• 对于行列式性质和定理的理解不够深入，例如混淆行列式的值与矩阵的秩，或者混淆行列式的值与矩阵的特征值等；
• 对于行列式应用题目的理解不够清晰，例如错误地判断方程组是否有解、错误地求解矩阵的逆等。

为了避免这些错误，需要在学习过程中注重细节，多加练习，并结合具体的应用场景进行思考和实践。