离散数学
离散数学是研究各种各样的离散量的结构及离散量之间的关系一门学科,是计算机科学中基础理论的核心课程。
什么是连续变量?
在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值,其数值只能用测量或计量的方法获取

离散变量是指其数值只能用自然数或证书单位计算的则为离散变量
例如,企业个数,职工人数,设备台数等,只能按计量单位数技术,这种变量的取值一般用计数方法取得

随着信息时代的到来,公共革命时代以微积分为代表的连续数学占主流的地位已经发生了变化,离散数学的重要性逐渐被人们认识
离散数学的特点
离散型
- 离散数学所研究的对象均是离散形式的,而不是连续的
- 如真假值、自然数、有限元素,线段等,这是由计算机的特点所决定的
- 计算机的结构是离散的(硬件:晶体管,集成块,元件,部件,设备;软件:程序,语句,符号)计算机所服务的对象均是离散的,而对连续对象计算机是无能为力的
能行性
- 离散数学所研究的问题均是能新的,能在计算机上求解
- 传统的数学分析以及数学分析为基础的各数学分支,如微分方程,实变函数,复变函数等均是研究连续变量的问题,对算法根本不予考虑或考虑很少

高度抽象性
- 数学的两个特点:抽象性,精确性
- 本课程除为后继课程打下坚实的基础和提供工具外,还未进一步研究计算机科学领域新课题创造条件,培养和提高抽象思维和缜密的概括能力,以及逻辑推理能力
离散数学的解决什么问题?
有三个非常聪明的学生!
一天老师给他们出了一个题,老师在每个人额头上贴了一张纸条并告诉他们,每个人纸条上都写了一个正整数,且某两个数的和等于第三个!(每个人可以看见另两个数,但看不见自己的)
老师问第一个学生,你能猜出自己的数吗?
回答:不能,问第二个,不能,第三个不能
再问第一个,不能,第二个,不能,第三个,我猜出来了,是26!请问你能猜出另外两个人额头的数吗


五个海盗抢到了100颗宝石,每一颗都一样的大小和价值连城,他们决定这么分
- 抽签决定自己的好嘛1 2 3 4 5
- 首先,由1号提出分配方案,然后大家5人表决,当且仅当达到半数的的人同意时,按照他的提案进行分配,否则他将被扔入大海喂鲨鱼
- 如果1号被喂鲨鱼,则由2号提出分配方案,然后大家4人进行表决,当且仅当达到半数的人同意时,按照他的提案进行分配,否则他将被扔入大海喂鲨鱼
- 以此推类,直到最终得出一个有效的分配方案
条件:每个海盗都是很聪明的人,都很理智且不讲感情
问题:假如你是1号海盗,你应该提出什么样的分配方案可以使自己的收益最大化?

一家6口爸爸,妈妈, 2个儿子,2个女儿还有一个警察和一个犯人过河!
- 河里有一条船一次坐两人
- 只有警察,爸爸,妈妈 才能撑船
- 警察不在犯人会伤害一家6口
- 爸爸不在妈妈会伤害儿子
- 妈妈不在爸爸会伤害女儿
有什么方法都过去?
我觉得这个游戏的关键在与警察和小偷.主要是小偷可以独自一人在岸上,在开头和末尾都要用到这个条件.
假设从左岸移向右岸
1.警察小偷过去,警察回来
2.警察带小男孩1过去,警察小偷回来
3.父带小男孩2过去,父单独回来
4.父母同时过去,母亲回来
(这时左岸警察、小偷、母亲、女儿1、女儿2.右岸父亲、男孩1、男孩2)
5.警察小偷过去,父亲回来
6.父亲母亲过去,母亲回来
7.母亲带女儿1过去,警察小偷回来
(这时左岸有女儿2,警察小偷.右岸有母亲、女儿1、父、男孩1、男孩2)
8.警察带女儿2过去(留小偷独自在左岸),警察在回来
9.警察小偷过去.
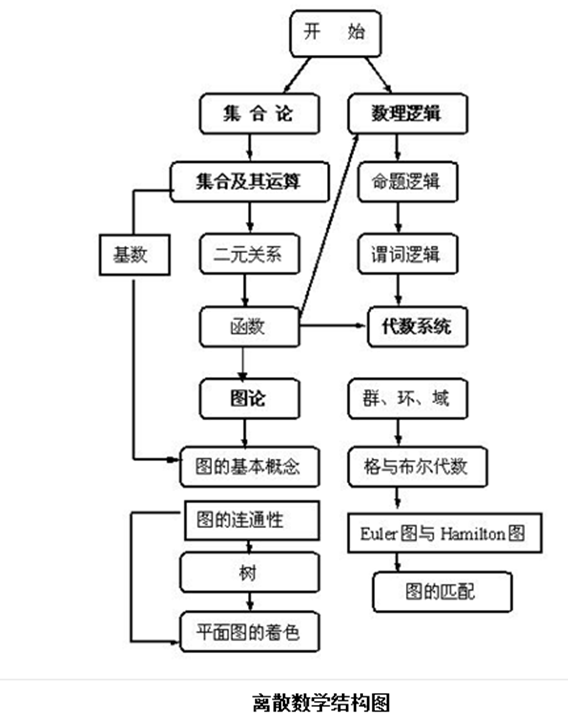
离散数学的构成
离散数学分为
- 数理逻辑
- 命题逻辑
- 谓词逻辑
- 集合论
- 集合
- 关系
- 函数
- 图论
- 组合数学
- 组合计数
- 容斥原理
- 递推求解
- 代数系统
- 代数系统的基本概念
- 代数系统的同态与同构
- 几个特殊代数系统内
离散数学结构图
第一部分 数理逻辑
什么是逻辑?
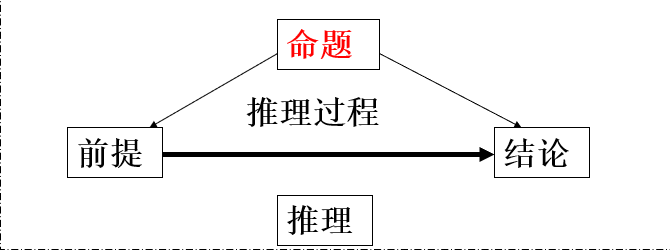
逻辑是人的一种抽象思维,是人通过概念、判断、推理、论证来理解和区分客观世界的思维过程
逻辑学是研究推理的学问


皇帝的新衣
故事中有两个裁缝告诉皇帝,他们缝制出的衣服有一种奇异得到功能:凡是不称职的人或者愚蠢的人都看不见这衣服
以上各项陈述都可以从裁缝的断言中逻辑地推出
除了
- 凡是不称职的人都不见这衣服
- 有些称职的人能够看见这衣服
- 凡是能够看见这衣服的人都是称职的人或者不愚蠢的人
- 凡是看不见这衣服的人都是不称职的人或者愚蠢的人
聪明的俘虏
问题:你来这里做什么?
回答的被认为是真话—被火烧死
回答的被认为是假话—被绞死
聪明的俘虏是如何回答的?
俘虏:我来这里是为了被绞死
数理逻辑
- 用户学方法研究推理的规律和形式的科学
- 推理:由一个或几个判断推出一个新判断的思维形式
- 数学方法:建立一套表意符号体系,对具体事物进行抽象的形势与研究方法
- 又称符号逻辑,逻辑学的一个分支

为什么需要数理逻辑
应用逻辑符号,可以把人类的推理过程分解成一些简单、原始、机械的步骤
- 使得用机器代替人类进行推理称为可能
- 提供程序员设计算法时的思维方法指导

数理逻辑
命题间的推理
第一部分 数理逻辑
- 命题逻辑基本概念
- 命题逻辑等值演算
- 命题逻辑的推理理论
- 一阶逻辑基本概念
- 一阶逻辑等值演算
第一章命题逻辑基本概念
- 命题与联结词
- 命题及其分类
- 联结词与复合命题
- 命题公式及其赋值
命题与真值
命题:判断结果唯一的陈述句
命题的真值:判断的结果
真值的取值:真与假
真命题与假命题
注意:感叹句、祈使句、疑问句都不是命题,陈述句中的悖论,判断结果不唯一确定的不是命题
例1:下列句子中哪些是命题?
(1) 是有理数**.** 假命题
(2) 2 + 5 = 7. 真命题
(3) x + 5 > 3. 不是命题
(4) 你去教室吗? 不是命题
(5) 这个苹果真大呀! 不是命题
(6) 请不要讲话! 不是命题
(7) 2050****年元旦下大雪 是命题,但是真值现在还不知道
(8) 我正在说假话**.** 悖论,不是命题
否定联结词与合取联结词
定义1.1 设p为命题,复合命题“非p(或p的否定)称为p的否定式,记作非p,符号非称为否定联结词,规定非p为真当且仅当p为假
定义1.2 设p、q为两个命题,复合命题“p并且q”或p与q陈薇p与q的合取式,记作p交q ∧ 称为合取联结词,规定p∧q为真当且仅当p与q同时为真
例****2 将下列命题符号化**.**
(1) 吴颖既用功又聪明**.**
(2) 吴颖不仅用功而且聪明**.**
(3) 吴颖虽然聪明,但不用功**.**
(4) 张辉与王丽都是三好生**.**
(5) 张辉与王丽是同学.
p:吴颖用功 q:吴颖聪明
p ∧q
p ∧q
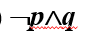
设p:张辉是三好生 q:王丽是三好生 p∧q
p:张辉与王丽是同学
1-3 其实是描述了合取式的灵活性与多样性
4-5要求分清与所链接的成分
析取联结词
定义1.3 设p、q为两个命题,复合命题p或q称作p与q的析取式,记作
p∨q,∨称作析取联结词,规定p∨q为假当且仅当p与q同时为假
例****3 将下列命题符号化
(1) 2 或 4 是素数**.**
(2) 2 或 3 是素数**.**
(3) 4 或 6 是素数**.**
(4) 小元元只能拿一个苹果或一个梨**.**
令p:2是素数 q:4是素数 p∨q
第四题:令p:小元拿一个苹果,q:小元拿一个梨
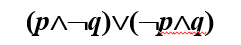
1-3为相容或,4为排斥或
蕴含联结词
定义1.4 设p、q为两个命题,符合命题“如果p,则q”称作p与q的蕴含式,记作→,并称p是蕴含式的前件,q为蕴含式的后件,→称为蕴含联结词,规定p→q为假当且仅当p为真q为假
- p→q的逻辑关系:q为p的必要条件,p是q的充分条件
- 当p为假时,p→q恒为真,称为空证明
- 常出现的错误:分不清充分条件与必要条件
在自然语言里,特别是在数学中,q是p的必要条件有许多不同的叙述方式,例如“只要p就q”,因为p所以q,p仅当q,只有q才p,除非q才p,除非q,否则非p等
当p为假时,为什么规定无论q是真是假,p→q都为真呢?这是一种善意的推断,譬如,说“如果天阳从西边出来,我就不姓张”实际上,不管是我否姓张,这句话都是对的。因为太阳不可能从西边出来,也就是说,前件:太阳从西边出来“为假,不论后件我不信张是真是假,这句话都是对的
在自然语言里,如果p则q中的前件p与后件q往往具有某种内在联系,而数理逻辑是研究抽象的形式推理,p与q可以无任何内在联系
蕴含联结词的实例
例****4 设 p**:天冷,q:小王穿羽绒服,将下列命题符号化**
(1) 只要天冷,小王就穿羽绒服**.**
(2) 因为****天冷,所以小王穿羽绒服.
(3) 若小王不穿羽绒服,则天不冷**.**
(4) 只有天冷,小王才穿羽绒服**.**
(5) 除非天冷,小王才穿羽绒服**.**
(6) 除非小王穿羽绒服,否则天不冷**.**
(7) 如果天不冷,则小王不穿羽绒服**.**
(8) 小王穿羽绒服仅当天冷的时候**.**
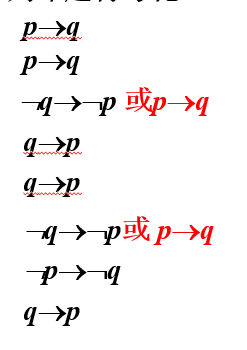
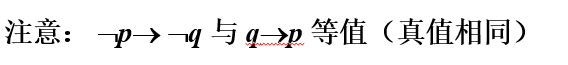
等价联结词
定义1.5 设p,q为两个命题,符合命题“p当且仅当q”称作p与q的等价式,记作p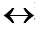 q,
q, 称为等价联结词,规定p等价q为真当且仅当
称为等价联结词,规定p等价q为真当且仅当
p与q同时为假或同时为真
p q的逻辑关系:p与q互为充分必要条件
q的逻辑关系:p与q互为充分必要条件
例5:求下列符合命题的真值
(1) 2 + 2 = 4 当且仅当 3 + 3 = 6.
(2) 2 + 2 = 4 当且仅当 3 是偶数**.**
(3) 2 + 2 = 4 当且仅当 太阳从东方升起**.**
(4) 2 + 2 = 4 当且仅当 美国位于非洲**.**
(5) 函数 f (x) 在 x****0 可导的充要条件是 它在 x****0 连续**.**
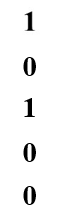
小结
- 本小节中p、q、r均表示命题
- 联结词集为
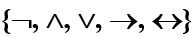 ,
,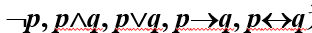
为基本复合命题,其中特别要注意理解p→q的含义,多次使用,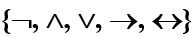 中的联结词组成更为复杂的符合命题
中的联结词组成更为复杂的符合命题
设p:根号2是无理数,q:3是奇数
r:苹果是方的,s:太阳绕地球转
则复合命题

联结词的运算顺序: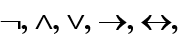
同级从左到右顺序进行,最先,按照从内到外顺序进行
1.2命题公式及其赋值
命题变项与合式公式
- 命题变项
- 合式公式
- 合式公式的层次
公式的赋值
- 公式赋值
- 公式类型
- 真值表
命题常项
命题变项(命题变元),命题变项不是命题
常项与变项均用p,q,r ,pi,qi,ri,等表示
定义1.6合式公式(简称公式)的递归定义
- 单个命题变项和命题常项都是合式公式,称作原子命题公式
- 若A是合式公式,则非A也是
- 若A,B是合式公式,则
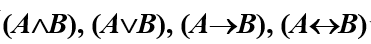
也是
- 只有有限次的应用1-3形成的符号串才是合式公式
几点说明:归纳或地规定定义,外层括号可以省去
合式公式的层次
定义1.7
- 若公式A是单个命题变项,则称A为0层公式
- 称A是n+1(n>=0)层公式是指下面情况之一
- A=非B,B是n层公式
- A=B^c,其中b,c分为为i层和j层公式,且n=max(i,j)
- A=B∪c,其中b,c的层级同b
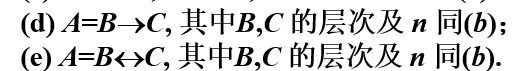
- 若公式A的层次为K,则称A为K层公式
例如,
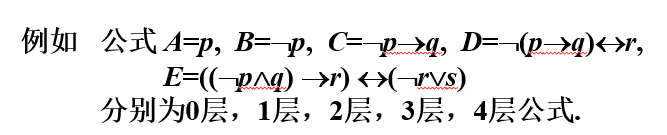
公式的赋值
定义1.8设p1,p2,…,pn是出现在公式A中的全部命题变项,给p1,p2,…,pn各指定一个真值,称为对A的一个赋值或解释,若赋值使A为1,则称这组值为A的成真赋值;若赋值使A为0,则称这组值为A的成假赋值
几点说明
-
A中仅出现p1,p2…pn,给A赋值a=a1a2…an是指p1=a1,p2=a2,p3=a3…pn=an,ai=0或1,ai之间不加标点符号
-
A中仅出现p,q,r…给A赋值a1a2a3,是指p=a1,q=a2,r=a3
-
含n个命题变项的工时有2的n次方个赋值
如000,010,101,110是
的成真赋值,
001,011,100,111是成假赋值
真值表
定义1.9将命题公式A在所有赋值下取值的情况列成表,称作A的真值表
构造真值表的步骤
- 找出公式中所含的全部命题变项p1,p2…pn若无下角标则按字母顺序排列,列出2^n个全部赋值,从00…0开始,按二进制加法,每次加一,直到11…1为止
- 按从低到高的顺序写出公式的各个层次
- 对每个赋值以此计算各层次的真值,直到最后计算出公式的真值为止
例****6 写出下列公式的真值表**,** 并求它们的成真赋值和成假
赋值**😗*
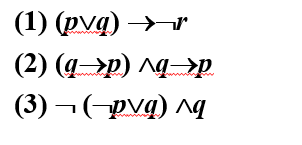
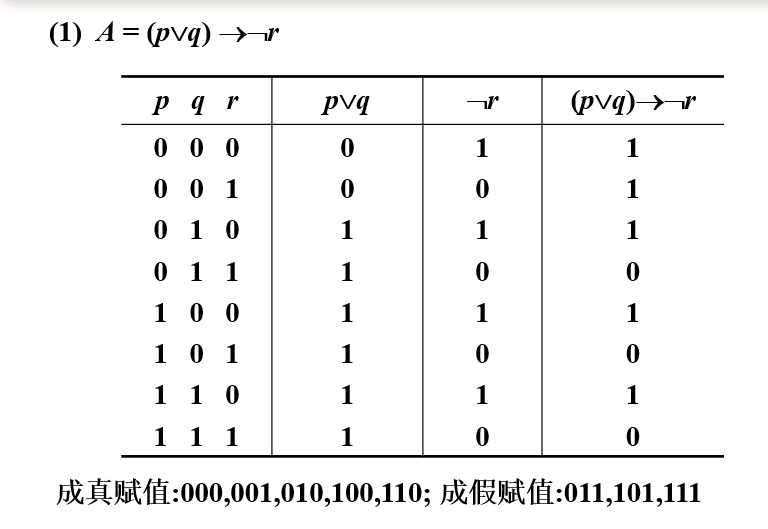
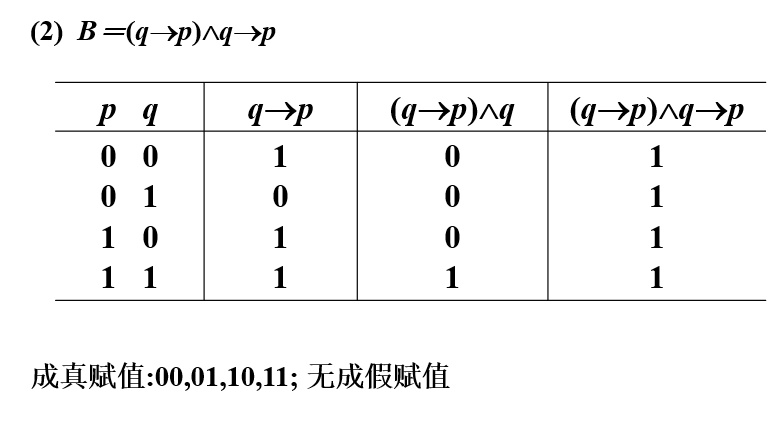
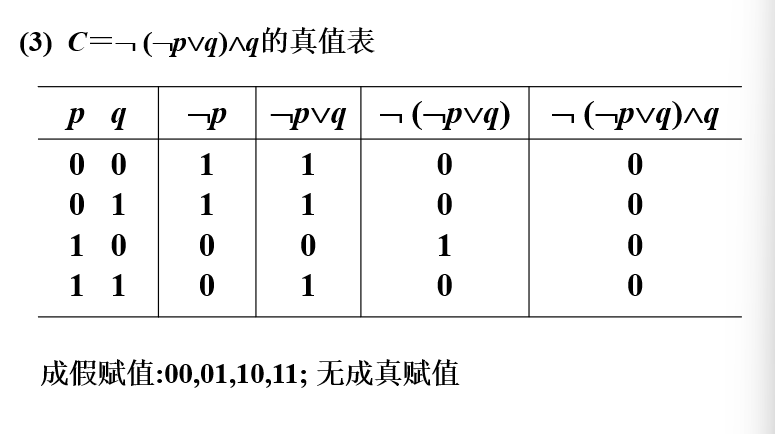
公式的类型
定义1.10
- 若A在他的任何赋值下均为真,则称A为重言式或永真式
- 若A在他的任何赋值下均为假,则称A为矛盾式或永假式
- 若A不是矛盾式,则称A是可满足式

真值表的用途:求出公式的全部成真赋值与成假赋值,判断公式的类型
第一章 习题课
主要内容
- 命题、真值、简单命题与复合命题、命题符号化
- 联结词
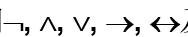 及复合命题符号化
及复合命题符号化 - 命题公式及层次
- 公式的类型
- 真值表及应用
基本要求
- 深刻理解各联结词的逻辑关系,熟练的将命题符号化
- 会求符合命题的真值
- 深刻理解合式公式及重言式、矛盾式、可满足式等概念
- 熟练的求公式的真值表,并用他求公式的成真赋值与成假赋值及判断 公式类型
练习1
1. 将下列命题符号化
(1) 豆沙包是由面粉和红小豆做成的**.**
(2) 苹果树和梨树都是落叶乔木**.**
(3) 王小红或李大明是物理组成员**.**
(4) 王小红或李大明中的一人是物理组成员**.**
(5) 由于交通阻塞,他迟到了**.**
(6) 如果交通不阻塞,他就不会迟到**.**
(7) 他没迟到,所以交通没阻塞**.**
(8) 除非交通阻塞,否则他不会迟到**.**
(9) 他迟到当且仅当交通阻塞**.**
提示,分清楚符合命题与简单命题,分清相容或与排斥或,分清必要条件,充分条件及充分必要条件
练习2
设p:2是素数
q:四川的省会是成都
r:太阳从西边出来
求下面命题的真值


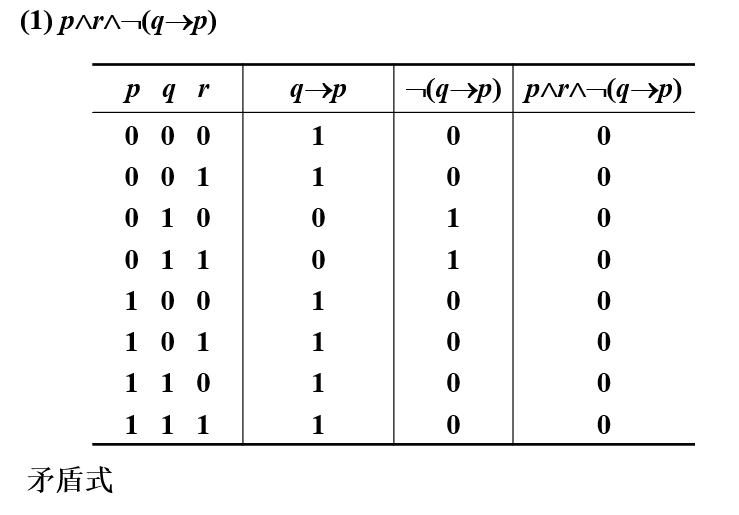
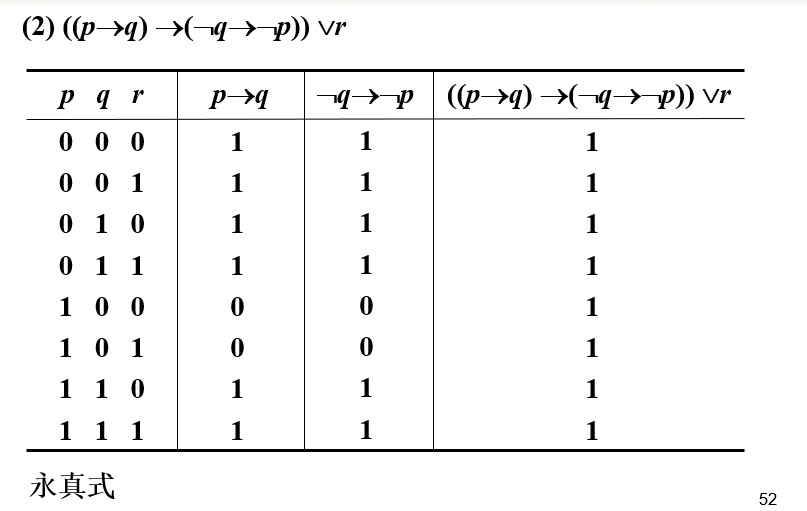
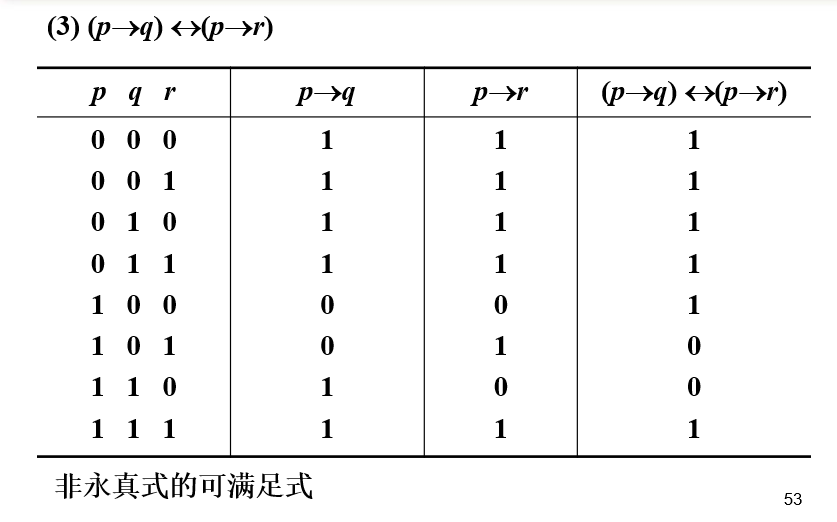



![观察者设计模式(Observer Design Pattern)[论点:概念、组成角色、相关图示、示例代码、框架中的运用、适用场景]](https://img-blog.csdnimg.cn/2494a74a45d9427eb407be9fa6702265.png)