我们了解到不同的物理器件，它们的访问速度是不一样的：速度快的往往代价高、容量小；代价低且容量大的，速度通常比较慢。为了充分发挥各种器件的优点，计算机存储数据的物理器件不会只选择一种，而是以 CPU 为核心，由内而外地组建了一整套的存储体系结构。它将各种不同的器件组合成一个体系，让各种器件扬长避短，从而形成一种快速、大容量、低成本的内存系统。而我们要想写出高性能的程序，就必须理解这个存储体系结构，并运用好它。

存储体系结构的核心

作为程序员，我们肯定是希望有无限资源的快速存储器，来存放程序的数据。而现实是，快速存储器的制造成本很高，速度慢的存储器相对便宜。所以从成本角度来说，计算机的存储结构被设计成分层的，一般包括寄存器、缓存、内存、磁盘等。

其中，缓存又是整个存储体系结构的灵魂，它让内存访问的速度接近于寄存器的访问速度。所以，要想深入理解存储体系结构，我们就要围绕“缓存”这个核心来学习。

在过去的几十年，处理器速度的增长远远超过了内存速度的增长。尤其是在 2001～2005年间，处理器的时钟频率在以 55% 的速度增长，而同期内存速度的增长仅为 7%。为了缩小处理器和内存之间的速度差距，缓存被设计出来。

我们说，距离处理器越近，访问速度就越快，造价也就越高，同时容量也会更小。缓存是处理器和内存之间的一个桥梁，通常分为多层，包括 L1 层、L2 层、L3 层等等。缓存的速度介于处理器和内存之间，访问处理器内部寄存器的速度在 1ns 以内（一个时钟周期），访问内存的速度通常在 50～100ns（上百个时钟周期）之间。那么对于缓存来讲，靠近处理器最近的 L1 层缓存的访问速度在 1ns～2ns（3 个时钟周期）左右，外层 L2 和 L3 层的访问速度在 10ns～20ns（几十个时钟周期）之间。

根据程序的空间局部性和时间局部性原理，一个处理得当的程序，缓存命中率要想达到 70～90% 并非难事。因此，在存储系统中加入缓存，可以让整个存储系统的性能接近寄存器，并且每字节的成本都接近内存，甚至是磁盘。

可见缓存结合了寄存器速度快和内存造价低的优点，是整个存储体系的灵魂之所在。明白了这一点后，接下来我们拆解一下缓存的物理架构。

缓存的物理架构

缓存是由 SRAM（静态随机存储）组成的，它的本质是一种时序逻辑电路，具体的每个单元（比特）由一个个锁存器构成，锁存器的功能就是让电路具有记忆功能。SRAM 的单位造价还是比较高的，而且要远高于内存的组成结构“DRAM（动态随机存储）”的造价。这是因为要实现一个锁存器需要六个晶体管，而实现一个 DRAM 仅需要一个晶体管和一个电容，但是 DRAM 因为结构简单，单位面积可以存放更多数据，所以更适合做内存。为了兼顾这两者的优缺点，于是它们中间需要加入缓存。

在制造方面，DRAM 因为有电容的存在，不再是单纯的逻辑电路，所以不能用 CMOS 工艺制造，而 SRAM 可以。这也是为什么缓存可以集成到芯片内部，而内存是和芯片分开制造的。

在了解了缓存的内部构成之后，我们再来看看缓存是怎样集成到芯片上的。

缓存集成到芯片的方式有多种。在过去的单核时代，处理器和各级缓存都只有一个，因此缓存的集成方式相对单一，就是把处理器和缓存直接相连。2004 年，Intel 取消了 4GHz奔腾处理器的研发计划，这意味着处理器以提升主频榨取性能的时代结束，多核处理器开始成为主流。

在多核芯片上，缓存集成的方式主要有以下三种：

集中式缓存：一个缓存和所有处理器直接相连，多个核共享这一个缓存；

分布式缓存：一个处理器仅和一个缓存相连，一个处理器对应一个缓存；

混合式缓存：在 L3 采用集中式缓存，在 L1 和 L2 采用分布式缓存。

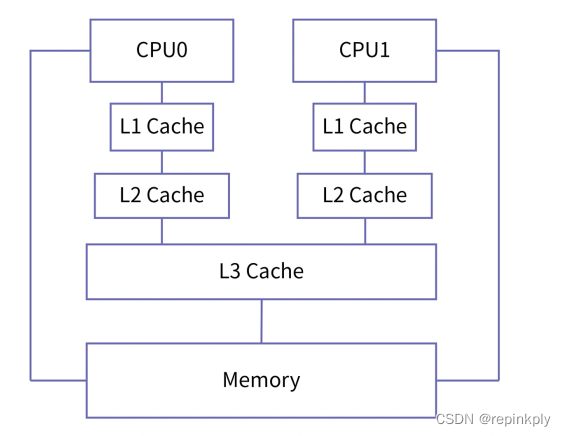
 现代的多核处理器大都采用混合式的方式将缓存集成到芯片上，一般情况下，L3 是所有处理器核共享的，L1 和 L2 是每个处理器核特有的。了解了缓存的物理架构后，我们来看一下缓存的工作原理。

缓存的工作原理

首先，我们来理解一个概念，cache line。cache line 是缓存进行管理的一个最小存储单元，也叫缓存块。从内存向缓存加载数据也是按缓存块进行加载的，一个缓存块和一个内存中相同容量的数据块（下称内存块）对应。这里，我们先从如何管理缓存块的角度，来看下缓存块的组织形式：

 上图中的小方框就代表一个缓存块。从图中，你也可以看到，整个缓存由组（set）构成，
每个组由路（way）构成。所以整个缓存容量等于组数、路数和缓存块大小的乘积：

整个缓存容量 = 组数 × 路数 × 缓存块大小

为了简化寻址方式，内存地址确定的数据块总是会被放在一个固定的组，但可以放在组内的任意路上，也就是说，对于一个特定地址数据的访问，它如果要载入缓存，那么它放在上图中的行数是固定的，但是具体放到哪一列是不固定的。根据缓存中组数和路数的不同，我们将缓存的映射方式分为三类：

直接相连映射：缓存只有一个路，一个内存块只能放置在特定的组上；
全相连映射：缓存只有一个组，所有的内存块都放在这一个组的不同路上；
组组相连映射：缓存同时由多个组和多个路。

对于直接相连映射，当多个内存块映射到同一组时，会产生冲突，因为只有一列，这个时候就需要将旧的缓存块换出，同时将新的缓存块放入，所以直接相连映射会导致缓存块被频繁替换。

而全相连映射可以在很大程度上避免冲突，不过，当要查询某个缓存块时，需要逐个遍历每个路，而且电路实现也比较困难。一个折中的办法就是，采用组组相连映射。这种方式与直接相连映射相比，产生冲突的可能性更小，与全相连映射相比，查询效率更高，实现也更简单。

上面的举例比较简单，我们再来看这样一种情况：缓存的组数一直是 2^n。虽然组数为 2^n 利于查询和定位，但是如果一个程序刚好以 2^n 间隔寻址，就会导致地址更多的被映射到同一个组，而另外一些组就会被映射得很少。因此，也有些缓存的组数会设计成一个质数，这样即便程序以 2^n间隔寻址，落到相同组的可能性会大大减小，这样一来，缓存各个组的利用率就会相对均衡。

那一个内存块具体是怎样映射到一个缓存块的呢？我们先来看看缓存块的内部结构：

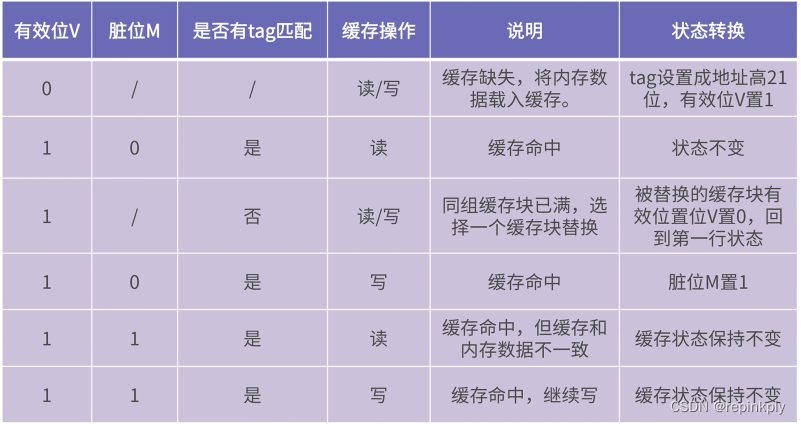
其中，V（valid）表示这个缓存块是否有效，或者说是否正在被使用；M（modified）表示这个缓存块是否被写，也就是“脏”位；B 表示缓存块的 bit 个数。 

假设要寻址一个 32 位的地址，缓存块的大小是 64 字节，缓存组织方式是 4 路组相连，缓存大小是 8K。经过计算我们得到缓存一共有 32 个组（ 8 × 1024 ÷ 64 ÷ 4 = 32 ）。那么对于任意一个 32 位的地址 Addr ，它映射到缓存的组号（set index）为 Addr 对组数32 取模，组号同时也等于 Addr 的第 6~10 位（ (Addr >> 6) & 0x1F ），Addr 的低 6位很好理解，它是缓存块的内部偏移（ 2^6 为 64 字节），那么高 21 位是用来干嘛的呢？我们接着往下看。

确定需要被映射到哪个组之后，我们需要在该组的路中进行查询。查询方式也很简单，直接将每个缓存块 tag 的 bit 位和地址 Addr 的高 21 位逐一进行匹配。如果相等，就说明该内存块已经载入到缓存中；如果没有匹配的 tag，就说明缓存缺失，需要将内存块放到该组的一个空闲缓存块上；如果所有路的缓存块都正在被使用，那么需要选择一个缓存块，将其移出缓存，把新的内存块载入。

上面这个过程涉及到缓存块状态转换，而状态转换又涉及到有效位 V、脏位 M、标签tag。总体来讲，缓存的状态转换有以下几种情况：

这里我们提到了缓存块替换，当同组的缓存块都被用完时，需要选择一个缓存块被换出，那么应该选谁被换出呢？这就和缓存块替换策略有关了。

缓存块替换策略

缓存块替换策略需要达到的一个目标是：被替换出的数据块应该是将来最晚会被访问的块。然而，对将来即将发生的事情是没有办法预测的，因为处理器并不知道程序将来会访问哪个地址。因此，现在的缓存替换策略都采用了最近最少使用算法（Least Recently Used ，LRU）或者是类似 LRU 的算法。

LRU 的原理很简单，比如程序要顺序访问 B1 、B2、B3、B4、B5 这几个地址块，并且这几个缓存块都映射到缓存的同一个组，同时我们假设缓存采用 4 路组组相连映射，那么当访问 B5 时，B1 就需要被替换出来。要实现这一点，有很多种方式，其中最简单也最容易实现的是利用位矩阵来实现。

首先，我们定义一个行、列都与缓存路数相同的矩阵。当访问某个路对应的缓存块时，先将该路对应的所有行置为 1，然后再将该路对应的所有列置为 0。最终结果体现为，缓存块访问时间的先后顺序，由矩阵行中 1 的个数决定，最近最常访问缓存块对应行 1 的个数最多。

假设现在一个四路相连的缓存组包含数据块 B1、B2、B3、B4, 数据块的访问顺序为 B2、B3、B1、B4，那么 LRU 矩阵在每次访问后的变化如下图所示：

 

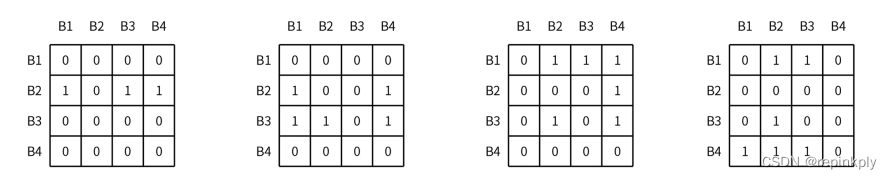
你会发现，最终 B2 对应行的 1 的个数最少，所以 B2 将会被优先替换。

在理解了缓存结构和它的工作原理以后，我们就可以来讨论核心内容了：如何正确地使用缓存，才可以写出高性能的程序？

缓存对程序性能的影响

通过前面的分析，我们已经知道，CPU 将未来最有可能被用到的内存数据加载进缓存。如果下次访问内存时，数据已经在缓存中了，这就是缓存命中，它获取目标数据的速度非常快。如果数据没在缓存中，这就是缓存缺失，此时要启动内存数据传输，而内存的访问速度相比缓存差很多。所以我们要避免这种情况。下面，我们先来了解一下哪些情况容易造成缓存缺失，以及具体会对程序性能带来怎样的影响。

缓存缺失

缓存性能主要取决于缓存命中率，也就说缓存缺失（cache miss）越少，缓存的性能就越好。一般来说，引起缓存缺失的类型主要有三种：

强制缺失：第一次将数据块读入到缓存所产生的缺失，也被称为冷缺失（cold miss），因为当发生缓存缺失时，缓存是空的（冷的）；

冲突缺失：由于缓存的相连度有限导致的缺失；

容量缺失：由于缓存大小有限导致的缺失。

第一类强制缺失最容易理解，因为第一次将数据读入缓存时，缓存中不会有数据，这种缺失无法避免。

第二类冲突缺失是因为相连度有限导致的，这里我用一个例子给你说明一下。在这个例子中，第一步我们可以通过 getconf 命令查看缓存的信息：

wj@wj:~$ getconf -a | grep CACHE
LEVEL1_ICACHE_SIZE                 32768
LEVEL1_ICACHE_ASSOC                8
LEVEL1_ICACHE_LINESIZE             64
LEVEL1_DCACHE_SIZE                 32768
LEVEL1_DCACHE_ASSOC                8
LEVEL1_DCACHE_LINESIZE             64
LEVEL2_CACHE_SIZE                  262144
LEVEL2_CACHE_ASSOC                 4
LEVEL2_CACHE_LINESIZE              64
LEVEL3_CACHE_SIZE                  16777216
LEVEL3_CACHE_ASSOC                 16
LEVEL3_CACHE_LINESIZE              64
LEVEL4_CACHE_SIZE                  0
LEVEL4_CACHE_ASSOC                 0
LEVEL4_CACHE_LINESIZE              0

在这个缓存的信息中，L1Cache（LEVEL1_ICACHE 和 LEVEL1_DCACHE 分别表示指令缓存和数据缓存，这里我们只关注数据缓存）的 cache line 大小为 64 字节，路数为 8 路，大小为 32K，可以计算出缓存的组数为 64 组（ 32K÷ 8 ÷ 64 = 64 ）。

第二步，我们使用一个程序来测试缓存的影响：

#include <stdio.h>
#include <stdlib.h>

#define M 64
#define N 10000000

int main(int argc,char* argv[]){
    
    printf("%ld\n",sizeof(long long));
    long long (*a)[N] = (long long(*)[N])calloc(M * N, sizeof(long long));

    for(int i = 0; i < 100000000; i++) {
        for(int j = 0; j < 4096; j+=512) {
            a[5][j]++;
        }
    }


    return 0;
}

上面代码中定义了一个二维数组，数组中元素的类型为 long long ，元素大小为 8 字节。所以一个 cache line 可以存放 64 ÷ 8 = 8 个元素。一组是 8 路，所以一组可以存放 8 × 8= 64 个元素。一路包含 64 个 cache line，因为前面计算出缓存的组数为 64，所以一路可以存放 8 × 64 = 512 个元素。

代码中的第一层循环是执行次数，第二层循环是以 512 为间隔访问元素，即每次访问都会落在同一个组内的不同 cache line ，因为一组有 8 路，所以我们迭代到 512 × 8 = 4096的位置。这样可以使同一组刚好可以容纳二层循环需要的地址空间。运行结果如下：

wj@wj:~/WORK/Learning/DT/C++$ gcc cache.c -o cache.out
wj@wj:~/WORK/Learning/DT/C++$ time ./cache.out 
8

real    0m1.213s
user    0m1.212s
sys     0m0.002s

第三步，当我们将第二层循环的迭代次数扩大一倍，也就是 8192 时，运行结果如下：

wj@wj:~/WORK/Learning/DT/C++$ gcc cache.c -o cache.out
wj@wj:~/WORK/Learning/DT/C++$ time ./cache.out 
8

real    0m7.938s
user    0m7.935s
sys     0m0.004s

虽然运算量增加了一倍，但运行时间却增加了 6 倍，相当于性能劣化三倍。劣化的根本原因就是当 i > 4096 时，也就是访问 4096 之后的元素，同一组的 cache line 已经全部使用，必须进行替换，并且之后的每次访问都会发生冲突，导致缓存块频繁替换，性能劣化严重。

第三类缓存容量缺失，可以认为是除了强制缺失和冲突缺失之外的缺失，也很好理解，当程序运行的某段时间内，访问地址范围超过缓存大小很多，这样缓存的容量就会成为缓存性能的瓶颈，这里要注意和冲突缺失加以区别，冲突缺失指的是在同一组内的缺失，而容量缺失描述范围是整个缓存。

程序局部性

//未完待续....