（一）、集合体系

单列集合：每次添加一个数据
双列集合：每次添加一对数据

集合体系结构：

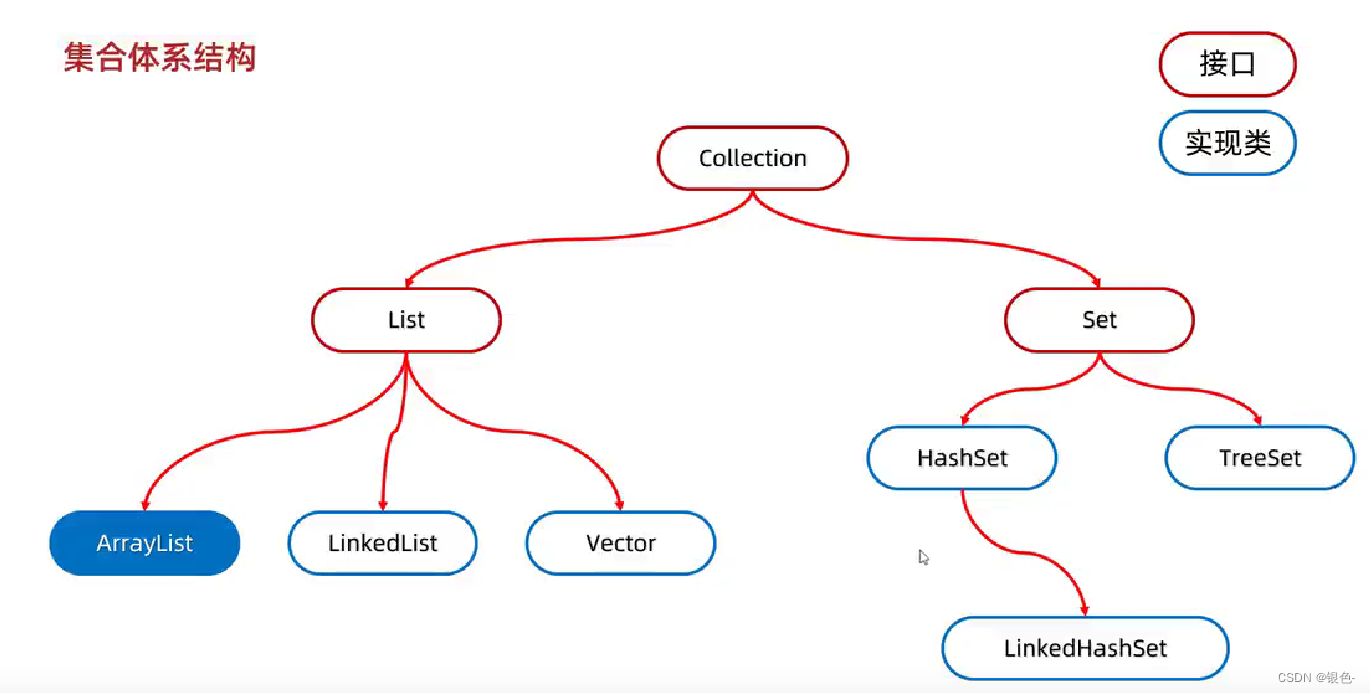
List系列集合：添加的元素是有序、可重复、有索引
有序：存和取的顺序一致
可重复：集合中存储的元素可以重复
有索引： 可以通过索引获取所有元素

Set系列集合：添加的元素是无序、不重复、无索引的元素

（二）、Collection

Collection是单列集合的顶级接口，它的功能所有的单列集合都可以继承使用

常用方法：

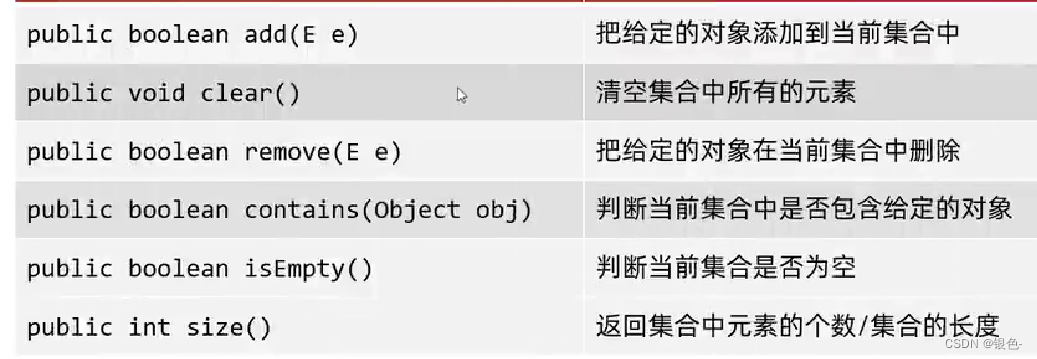
add的返回值：如果往List系列集合添加元素，那么返回值永远是true。如果往Set系列集合添加，如果数据不存在则返回true，反之则返回false

（三）、Collection的遍历方式

3.1迭代器

lterator类，是集合专用遍历方式，不依赖索引

常用方法：

注意点：

如果要第二次遍历，要获取一个新的迭代器对象
如果当前位置没有元素，还要强行调用next，会报错NoSuchElementException

3.2增强for遍历

底层还是一个迭代器
所有的单列集合和数组才能使用增强for遍历

格式：

快速生成：集合的名字.for +回车

注意细节：
修改增强for中的变量，不会改变集合中原本的数据

3.3 Lambda表达式遍历

最简化方式：集合名.forEach(s ->sout(s));

（四）、List

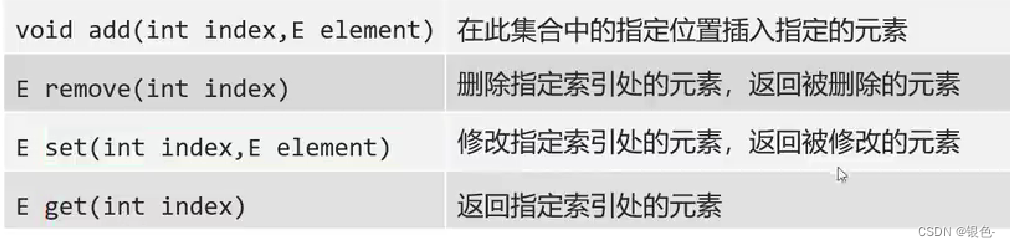
使用add时，如果原来索引的位置上有元素，这个元素会自动往后移

独有的遍历方式：

普通for循环：
集合名.size 表示长度
集合名.fori
i表示索引，利用索引获取元素

列表迭代器：ListInterator
额外添加了一个方法，在遍历过程中可以添加元素（用列表迭代器的add方法）

五种遍历方式对比：

（五）、数据结构

计算机底层存储、组织数据的方式
8种数据结构：栈，队列，数组，链表，二叉树，二叉查找树，平衡二叉树，红黑树

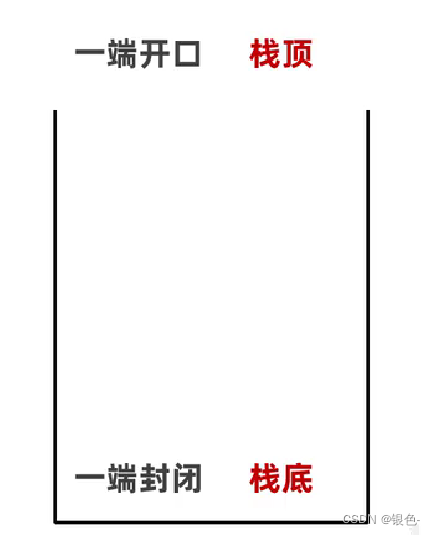
5.1 栈

特点：后进先出，先进后出
进入栈模型称为 ：进/压栈
离开栈模型称为 ：弹/出栈

5.2 队列

特点：先进先出，后进后出
从后端进入队列模型的过程称为：入队列
从前端离开队列模型的过程称为：出队列

后端进，前端出

5.3 数组

特点：
查询速度快
删除效率低
添加效率极低

5.4 链表

分为单向链表和双向链表（结点包含前一个结点的地址）

链表中的结点都是一个独立的对象，在内存中是不连续的
链表里的每个元素称为 ：结点（数据，下个结点的地址）

特点：查询慢，不管查询什么都要从头开始
增删比较快

5.5 树

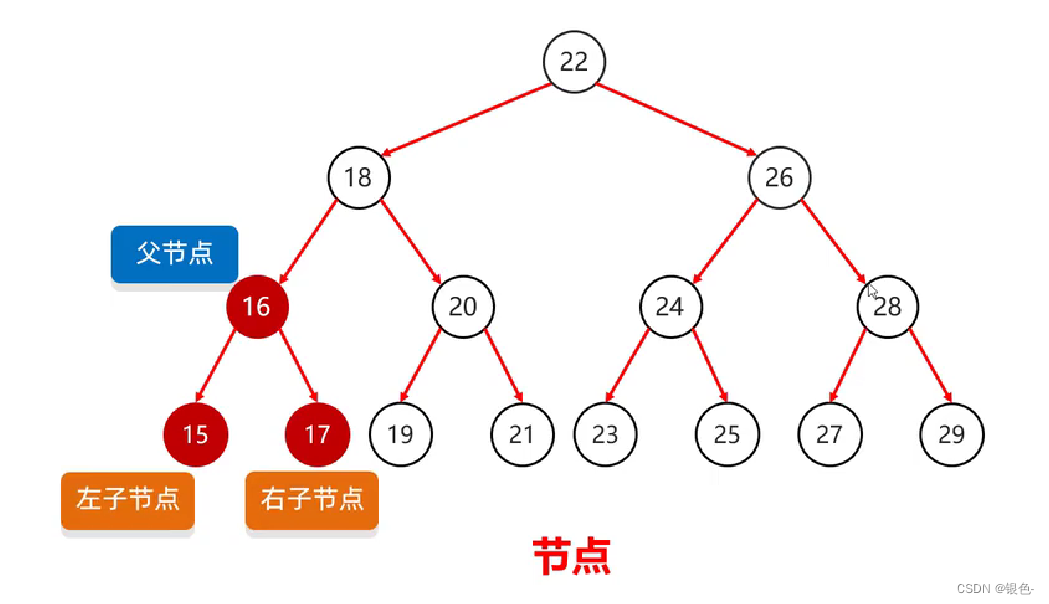
节点里有：父节点地址，值，左子节点地址，右子节点地址
度：每一个节点的子节点数量
树高：树的总层数
根节点：最顶层的节点
根节点的左右子树

二叉树：任意节点的度<=2

二叉查找树：

添加规则：大的存右边，小的存左边，一样的不存
遍历方式：
前序遍历：从根节点开始，按照当前节点，左子节点，右子节点的顺序遍历
中序遍历：左子节点，当前节点，右子节点
后序遍历：左，右，当前
层序遍历：从跟节点开始，一层一层遍历

平衡二叉树：
在二叉查找树上多一个规则：任意节点左右子树高度差不超过1

通过旋转机制保持平衡：当添加完节点不平衡时才会触发

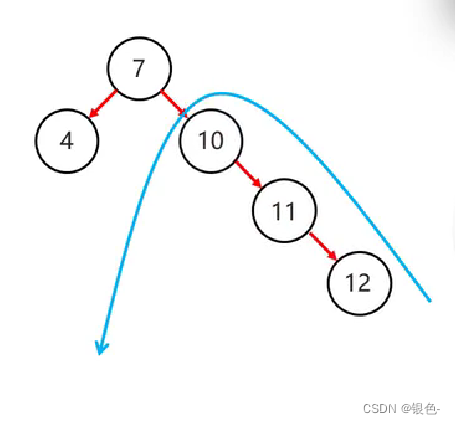
左旋：确定支点（从添加的节点开始找，第一个不平衡的点）

示例1：

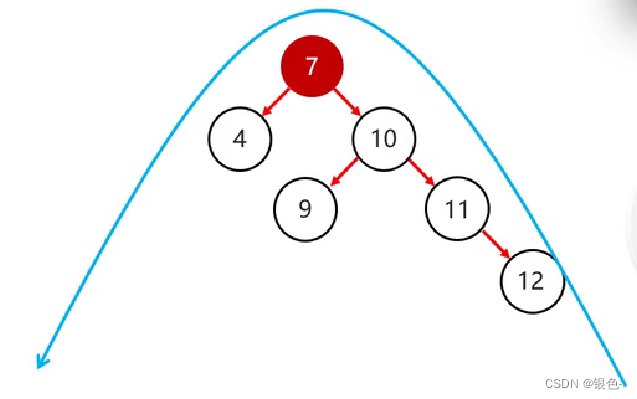
示例2：

右旋：

示例1：

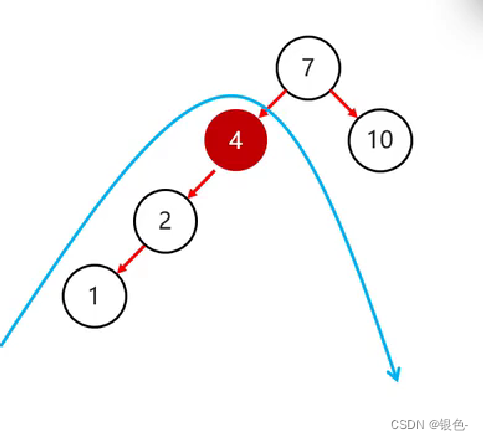
示例2：

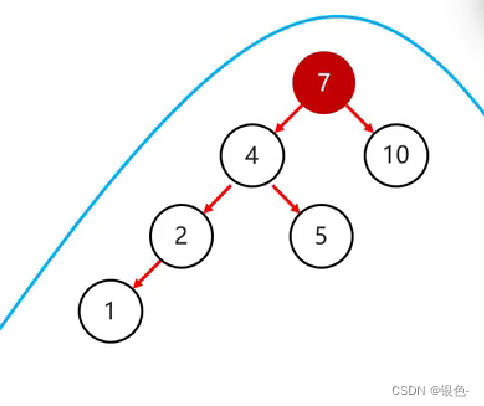
四种触发旋转机制的情况：
1.左左：当根节点左子树的左子树有节点插入，导致二叉树不平衡
一次右旋

2.左右：根节点左子树的右子树有节点插入，导致二叉树不平衡
局部左旋，一次右旋

3.右右：根节点右子树的右子树有节点插入
一次左旋

4.右左：根节点右子树的左子树有节点插入
局部右旋，一次左旋

5.6 红黑树

增删改查性能都很好
自平衡的二叉查找树，每一个节点上都有储存位表示节点的颜色
每一个节点可以是红或黑，它不是高度平衡的，它的平衡通过红黑规则实现

红黑规则：

添加的节点默认是红色的
调整方案：

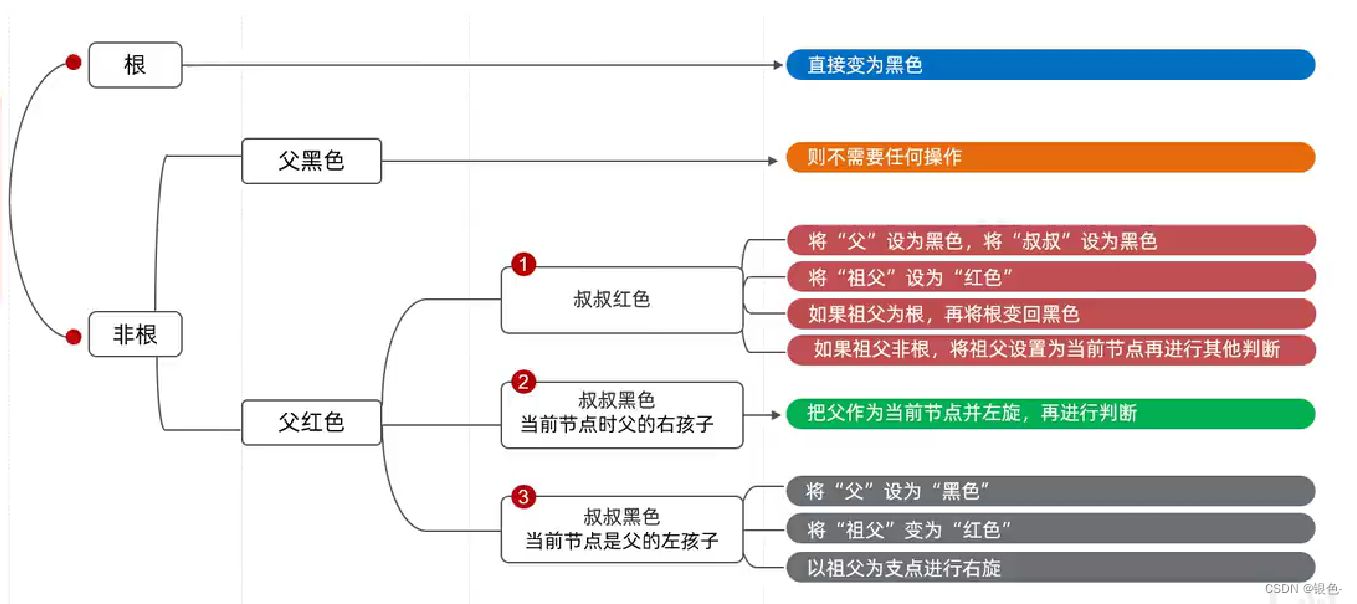
（六）、泛型

好处：

Java中的泛型是伪泛型，只在编译时期有效

注：如果不写泛型，默认类型是object
指定泛型类型后，传递数据时，可以传入该类类型或者其子类类型
可以写在类后面，方法上面，接口后面

泛型类：当一个类中，某个变量的数据类型不确定时，就可以定义带有泛型的类

泛型方法：方法中形参类型不确定时
1.使用类名后面定义的泛型（所有方法都能使用）
2.在方法声明上定义自己的泛型（只有本方法能使用）

泛型接口：

使用方式1：实现类给出具体的类型
使用方式2：实现类延续泛型，创建对象时再确定