（数字图像处理MATLAB+Python）第六章图像平滑-第二节：频域平滑滤波

news2024/11/18 2:29:14

文章目录

  • 一：理想低通滤波
    • （1）概述
    • （2）程序
  • 二：巴特沃斯低通滤波
    • （1）概述
    • （2）程序
  • 三：指数低通滤波
    • （1）概述
    • （2）程序
  • 四：梯形低通滤波
    • （1）概述
    • （2）程序

频域平滑滤波：是数字图像处理中常用的一种滤波方法，它的主要思想是在频域中对图像进行滤波处理。其步骤如下

  • 对原始图像进行傅里叶变换，得到频域图像
  • 对频域图像进行滤波操作，可以选择常用的低通滤波器，例如高斯低通滤波器、均值滤波器等
  • 对滤波后的频域图像进行傅里叶逆变换，得到平滑后的图像

在这里插入图片描述

频域低通滤波的核心关键为设计合适的低通滤波器 H ( u , v ) H(u,v) H(u,v)

G ( u , v ) = H ( u , v ) F ( u , v ) G(u,v)=H(u,v)F(u,v) G(u,v)=H(u,v)F(u,v)

频域平滑滤波有以下几类

  • 理想低通滤波
  • 巴特斯沃滤波
  • 指数低通滤波
  • 梯形低通滤波

一：理想低通滤波

（1）概述

理想低通滤波：是一种在频域中将高频信号滤除，保留低频信号的滤波器。其数学表达式为

H ( u , v ) = { 1 D ( u , v ) ≤ D 0 0 D ( u , v ) > D 0 H(u, v)=\left\{\begin{array}{ll}1 & D(u, v) \leq D_{0} \\0 & D(u, v)>D_{0}\end{array}\right. H(u,v)={10​D(u,v)≤D0​D(u,v)>D0​​

其中， H ( u , v H(u, v H(u,v)表示频域滤波器在 ( u , v ) (u,v) (u,v)处的值， D ( u , v ) = u 2 + v 2 D(u,v)=\sqrt{ u^{2}+v^{2} } D(u,v)=u2+v2 ​表示频域中点 ( u , v ) (u,v) (u,v)到中心点的距离， D 0 D_{0} D0​为截止频率，即在此频率以下的信号通过，此频率以上的信号被滤除

具体来说，可以通过对图像进行傅里叶变换，将图像转换到频域中。然后，将理想低通滤波器与频域图像做乘积，得到滤波后的频域图像。最后，对滤波后的频域图像进行反傅里叶变换，得到空域中的滤波结果

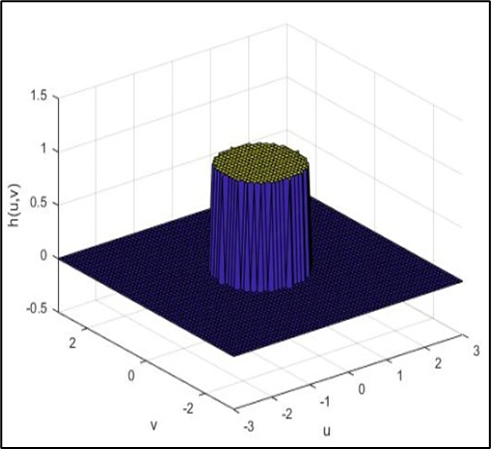
在这里插入图片描述

理想低通滤波器具有截止频率清晰、滤波效果好等优点，但由于其截止频率突变，会导致滤波结果出现“振铃”现象，同时也不适用于实际应用中，因为实际信号中的高频分量很难完全截止

  • “振铃”现象： H ( u , v ) H(u,v) H(u,v)在 D 9 D_{9} D9​处由1突变到0，其对应的冲激响应 h ( x , y ) h(x,y) h(x,y)在空域中表现为同心环形式；同心环半径与 D 0 D_{0} D0​成反比； D 0 D_{0} D0​越小，同心环半径越大，模糊越厉害

在这里插入图片描述

如下图为“振铃”现象

在这里插入图片描述

（2）程序

实现如下效果：截断频率不同的理想低通滤波器

在这里插入图片描述

matlab实现：

% 读入图像并显示
Image=imread('lena.bmp');
imshow(Image);

% 对图像进行傅里叶变换，并进行频谱搬移
FImage=fftshift(fft2(double(Image)));  

% 获取频域图像的大小
[N M]=size(FImage);

% 初始化一个全零的数组
g=zeros(N,M);

% 计算频谱的中心点坐标
r1=floor(M/2);  r2=floor(N/2);

% 在傅里叶频谱图上绘制4个圆形，并显示傅里叶频谱图像
figure;
imshow(log(abs(FImage)+1),[]),title('傅里叶频谱');
hold on
circle(r1,r2,5)
circle(r1,r2,11)
circle(r1,r2,45)
circle(r1,r2,68)

% 初始化截止频率数组
d0=[5 11 45 68];

% 循环对不同截止频率进行低通滤波并显示
for i=1:4
    for x=1:M
        for y=1:N
            % 计算当前像素点到频谱中心的距离
            d=sqrt((x-r1)^2+(y-r2)^2);
            % 根据距离和截止频率确定滤波器的值
            if d<=d0(i)
                h=1;
            else
                h=0;
            end
            % 用滤波器乘以频域图像
            g(y,x)=h*FImage(y,x);
        end
    end
    % 对滤波后的频域图像进行反傅里叶变换得到空域的图像，并显示
    g= real(ifft2(ifftshift(g)));
    figure,imshow(uint8(g)),title(['理想低通滤波D0=',num2str(d0(i))]);
end

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读入图像并显示
Image = cv2.imread('lena.bmp', cv2.IMREAD_GRAYSCALE)
plt.imshow(Image, cmap='gray')
plt.show()

# 对图像进行傅里叶变换，并进行频谱搬移
FImage = np.fft.fftshift(np.fft.fft2(Image.astype(float)))

# 获取频域图像的大小
N, M = FImage.shape

# 初始化一个全零的数组
g = np.zeros((N, M))

# 计算频谱的中心点坐标
r1 = int(M/2)
r2 = int(N/2)

# 在傅里叶频谱图上绘制4个圆形，并显示傅里叶频谱图像
plt.imshow(np.log(np.abs(FImage)+1), cmap='gray')
plt.title('傅里叶频谱')
plt.hold(True)
circle1 = plt.Circle((r1,r2), 5, color='r', fill=False)
circle2 = plt.Circle((r1,r2), 11, color='r', fill=False)
circle3 = plt.Circle((r1,r2), 45, color='r', fill=False)
circle4 = plt.Circle((r1,r2), 68, color='r', fill=False)
plt.gca().add_artist(circle1)
plt.gca().add_artist(circle2)
plt.gca().add_artist(circle3)
plt.gca().add_artist(circle4)
plt.show()

# 初始化截止频率数组
d0 = [5, 11, 45, 68]

# 循环对不同截止频率进行低通滤波并显示
for i in range(4):
    for x in range(M):
        for y in range(N):
            # 计算当前像素点到频谱中心的距离
            d = np.sqrt((x-r1)**2 + (y-r2)**2)
            # 根据距离和截止频率确定滤波器的值
            if d <= d0[i]:
                h = 1
            else:
                h = 0
            # 用滤波器乘以频域图像
            g[y,x] = h * FImage[y,x]
    # 对滤波后的频域图像进行反傅里叶变换得到空域的图像，并显示
    g = np.real(np.fft.ifft2(np.fft.ifftshift(g)))
    plt.imshow(g.astype(np.uint8), cmap='gray')
    plt.title('理想低通滤波D0=' + str(d0[i]))
    plt.show()

二：巴特沃斯低通滤波

（1）概述

巴特沃斯低通滤波：是一种用于去除图像中高频噪声的数字滤波方法。它是一种优化了幅频特性的滤波器，能够保留图像中更多的低频信息。该滤波器是基于巴特沃斯函数设计的，巴特沃斯函数是一种理想的低通滤波器，其频率响应具有非常陡峭的截止特性，但在实际应用中会出现一些缺陷。因此，巴特沃斯低通滤波器是基于巴特沃斯函数的特点，通过添加一些适当的补偿来消除其缺陷的一种优化滤波器

{ H ( u , v ) = 1 1 + [ D ( u , v ) / D 0 ] 2 n H ( u , v ) = 1 1 + ( 2 − 1 ) [ D ( u , v ) / D 0 ] 2 n \left\{\begin{array}{l}H(u, v)=\frac{1}{1+\left[D(u, v) / D_{0}\right]^{2 n}} \\H(u, v)=\frac{1}{1+(\sqrt{2}-1)\left[D(u, v) / D_{0}\right]^{2 n}}\end{array}\right. {H(u,v)=1+[D(u,v)/D0​]2n1​H(u,v)=1+(2 ​−1)[D(u,v)/D0​]2n1​​

当 D ( u , v ) = D 0 D(u,v)=D_{0} D(u,v)=D0​时， H ( u , v ) H(u,v) H(u,v)降为最大值的 1 2 \frac{1}{2} 21​或 1 2 \frac{1}{\sqrt{ 2 }} 2 ​1​

与其他低通滤波器相比，巴特沃斯低通滤波器有以下特点：

  • 具有更陡峭的截止特性，可以更好地去除高频噪声
  • 可以通过调整阶数和截止频率来灵活地控制滤波器的性能
  • 在频域中的实现相对简单，通常使用二阶滤波器级联实现

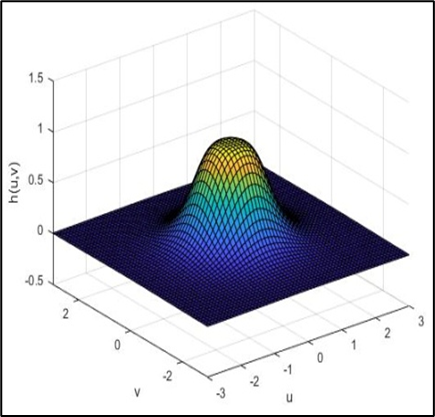
在这里插入图片描述

如下图所示，随着阶数 n n n的增加，图像振铃效应越来越明显

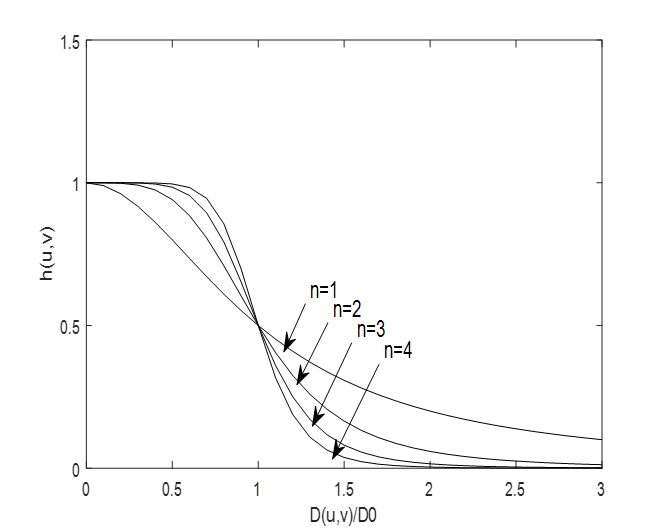
在这里插入图片描述

（2）程序

实现如下效果：阶数不同的巴特沃斯低通滤波器

在这里插入图片描述

matlab实现：

Image=imread('lena.bmp'); % 读取lena.bmp图像
Image=imnoise(Image,'gaussian'); % 加入高斯噪声
imshow(Image); % 显示噪声图像
FImage=fftshift(fft2(double(Image)));  % 对加噪声图像进行傅里叶变换及频谱搬移
[N M]=size(FImage); % 获取傅里叶变换后频率矩阵的大小
g=zeros(N,M); % 用0矩阵初始化滤波后的频率矩阵
r1=floor(M/2);  r2=floor(N/2); % 计算中心点位置
figure;
imshow(log(abs(FImage)+1),[]),title('傅里叶频谱'); % 显示傅里叶频谱
hold on
circle(r1,r2,30) % 在频谱图上绘制圆形滤波器的半径
d0=30; % 设置圆形滤波器的半径
n=[1 2 3 4]; % 不同的Butterworth滤波器阶数
for i=1:4
    for x=1:M
        for y=1:N
            d=sqrt((x-r1)^2+(y-r2)^2); % 计算像素点到中心点的距离
            h=1/(1+(d/d0)^(2*n(i))); % 计算Butterworth滤波器的值
            g(y,x)=h*FImage(y,x); % 对傅里叶变换后的频率矩阵进行滤波
        end
    end
    g=ifftshift(g); % 频谱搬移
    g=real(ifft2(g)); % 逆傅里叶变换得到滤波后的图像
    figure,imshow(uint8(g)),title(['Butterworth低通滤波n=',num2str(n(i))]); % 显示滤波后的图像
end

Python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并加入高斯噪声
Image = cv2.imread('lena.bmp', 0)
Image = cv2.GaussianBlur(Image, (5, 5), 0)
Image = Image.astype(np.float32)
Image += np.random.normal(0, 20, Image.shape)
Image = np.uint8(np.clip(Image, 0, 255))

# 显示噪声图像
plt.imshow(Image, cmap='gray')
plt.title('加噪声的图像')
plt.show()

# 对加噪声图像进行傅里叶变换并进行频谱搬移
FImage = np.fft.fftshift(np.fft.fft2(Image))

# 获取频域图像的大小
N, M = FImage.shape

# 初始化一个全零的数组
g = np.zeros((N, M))

# 计算频谱的中心点坐标
r1 = M // 2
r2 = N // 2

# 在傅里叶频谱图上绘制一个圆形，并显示傅里叶频谱图像
plt.imshow(np.log(np.abs(FImage) + 1), cmap='gray')
plt.title('傅里叶频谱')
plt.plot(r1, r2, 'wo', markerfacecolor='none', markersize=60)
plt.show()

# 初始化截止频率数组和Butterworth滤波器阶数数组
d0 = 30
n = [1, 2, 3, 4]

# 循环对不同Butterworth滤波器阶数进行低通滤波并显示
for i in range(4):
    for x in range(M):
        for y in range(N):
            # 计算当前像素点到频谱中心的距离
            d = np.sqrt((x - r1) ** 2 + (y - r2) ** 2)
            # 根据距离和截止频率计算Butterworth滤波器的值
            h = 1 / (1 + (d / d0) ** (2 * n[i]))
            # 用滤波器乘以频域图像
            g[y, x] = h * FImage[y, x]
    # 对滤波后的频域图像进行反傅里叶变换得到空域的图像，并显示
    g = np.real(np.fft.ifft2(np.fft.ifftshift(g)))
    plt.imshow(np.uint8(g), cmap='gray')
    plt.title('Butterworth低通滤波 n=' + str(n[i]))
    plt.show()

三：指数低通滤波

（1）概述

指数低通滤波：是一种在频域中对图像进行滤波的方法，主要用于去除高频噪声。该滤波器的核心思想是将频域中高频分量的值进行衰减，从而达到降低图像的高频部分，保留图像的低频部分的效果

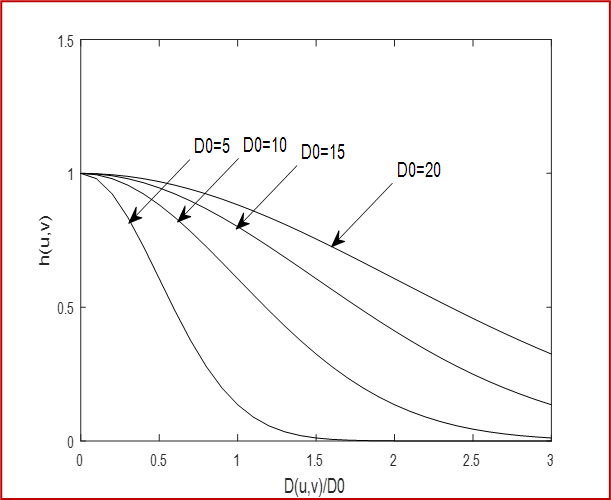
H ( u , v ) = e − D 2 ( u , v ) 2 D 0 2 H(u, v)=e^{-\frac{D^{2}(u, v)}{2 D_{0}^{2}}} H(u,v)=e−2D02​D2(u,v)​

其中， D ( u , v ) D(u,v) D(u,v)是频域中像素点 ( u , v ) (u,v) (u,v)到中心点的距离， D 0 D_0 D0​是滤波器的截止频率，也就是滤波器开始起作用的频率。 H ( u , v ) H(u,v) H(u,v)是滤波器在频域的值，它与原始图像在频域中的傅里叶变换进行卷积，即可得到滤波后的图像。当 D ( u , v ) = D 0 D(u,v)=D_{0} D(u,v)=D0​时， H ( u , v ) H(u,v) H(u,v)降为最大值的0.607处

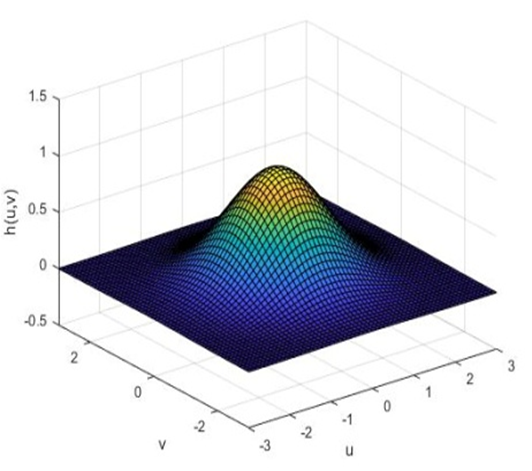
在这里插入图片描述

如下图所示，随着截止频率 D 0 D_{0} D0​的增加，图像振铃效应越来越不明显

在这里插入图片描述

（2）程序

实现如下效果：截止频率不同的指数低通滤波器
在这里插入图片描述

matlab实现：

Image=imread('lena.bmp');  %读取lena.bmp图像
Image=imnoise(Image,'gaussian');   %添加高斯噪声
imshow(Image);  %显示加噪声后的图像
FImage=fftshift(fft2(double(Image)));  %对图像进行傅里叶变换，并对频谱进行移位
[N M]=size(FImage);  %获取变换后频谱的大小
g=zeros(N,M);  %初始化滤波后的频谱
r1=floor(M/2);  r2=floor(N/2);  %获取频谱中心位置
figure;
imshow(log(abs(FImage)+1),[]),title('傅里叶频谱');  %显示傅里叶频谱
d0=[20 40];  %设置指数低通滤波器的参数
n=2;
for i=1:2  %遍历两个不同的截止频率
    for x=1:M
        for y=1:N
            d=sqrt((x-r1)^2+(y-r2)^2);  %计算距离
            h=exp(-0.5*(d/d0(i))^n);   %计算滤波器响应
            g(y,x)=h*FImage(y,x);  %对频谱进行滤波
        end
    end
    g=ifftshift(g);  %对滤波后的频谱进行移位
    g=real(ifft2(g));  %对滤波后的频谱进行逆傅里叶变换
figure,imshow(uint8(g)),title(['指数低通滤波D0=',num2str(d0(i))]);  %显示滤波后的图像
end

Python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取lena.bmp图像
Image = cv2.imread('lena.bmp', cv2.IMREAD_GRAYSCALE)

# 添加高斯噪声
Image = cv2.GaussianBlur(Image, (3, 3), 0)
Image = Image + np.uint8(np.random.normal(0, 20, size=Image.shape))

# 显示加噪声后的图像
plt.imshow(Image, cmap='gray')
plt.show()

# 对图像进行傅里叶变换，并对频谱进行移位
FImage = np.fft.fftshift(np.fft.fft2(np.double(Image)))

# 获取变换后频谱的大小
N, M = FImage.shape

# 初始化滤波后的频谱
g = np.zeros((N, M))

# 获取频谱中心位置
r1, r2 = M // 2, N // 2

# 显示傅里叶频谱
plt.imshow(np.log(np.abs(FImage) + 1), cmap='gray')
plt.title('傅里叶频谱')
plt.show()

# 设置指数低通滤波器的参数
d0 = [20, 40]
n = 2

# 遍历两个不同的截止频率
for i in range(2):
    for x in range(M):
        for y in range(N):
            # 计算距离
            d = np.sqrt((x - r1)**2 + (y - r2)**2)
            # 计算滤波器响应
            h = np.exp(-0.5 * (d / d0[i])**n)
            # 对频谱进行滤波
            g[y, x] = h * FImage[y, x]

    # 对滤波后的频谱进行移位
    g = np.fft.ifftshift(g)
    # 对滤波后的频谱进行逆傅里叶变换
    g = np.real(np.fft.ifft2(g))

    # 显示滤波后的图像
    plt.imshow(np.uint8(g), cmap='gray')
    plt.title('指数低通滤波D0=' + str(d0[i]))
    plt.show()

四：梯形低通滤波

（1）概述

梯形低通滤波：是一种可以在一定程度上同时平衡频率响应的振铃和带宽的低通滤波器。它的频率响应类似于一个梯形，因此得名。梯形低通滤波器可以用于图像处理中的频域滤波，通过控制梯形上下两条边界的斜率和距离，可以调整其截止频率和带宽。梯形低通滤波器相比于其他低通滤波器，可以提供更平滑的过渡区域和更宽的过渡带宽，从而减少了图像的失真和信息的丢失

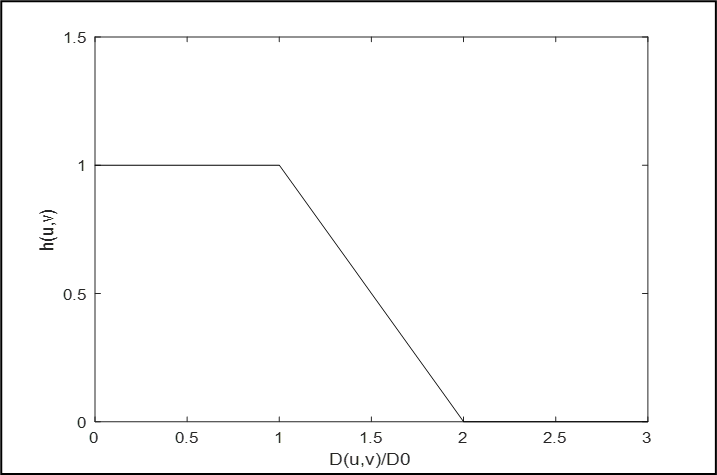
H ( u , v ) = { 1 , D ( u , v ) ≤ D 0 D ( u , v ) − D 1 D 0 − D 1 , D 0 < D ( u , v ) ≤ D 1 0 D ( u , v ) > D 1 H(u, v)=\left\{\begin{array}{cc}1, & D(u, v) \leq D_{0} \\\frac{D(u, v)-D_{1}}{D_{0}-D_{1}}, & D_{0}<D(u, v) \leq D_{1} \\0 & D(u, v)>D_{1}\end{array}\right. H(u,v)=⎩ ⎨ ⎧​1,D0​−D1​D(u,v)−D1​​,0​D(u,v)≤D0​D0​<D(u,v)≤D1​D(u,v)>D1​​

其中 D 0 D_{0} D0​为截止频率， D 0 、 D 1 D_{0}、D_{1} D0​、D1​需要满足： D 0 < D 1 D_{0}<D_{1} D0​<D1​

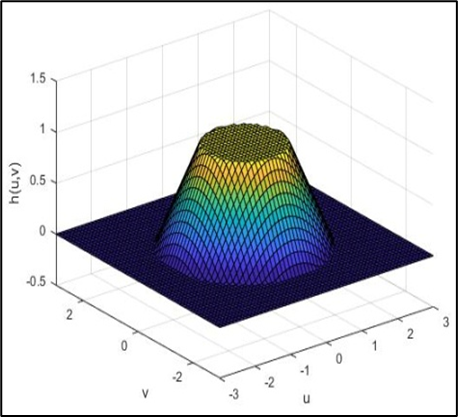
在这里插入图片描述

如下图所示

在这里插入图片描述

（2）程序

实现如下效果截止频率不同的梯度低通滤波器

在这里插入图片描述

matlab实现：

Image=imread('lena.bmp');
Image=imnoise(Image,'gaussian');   %加入噪声
imshow(Image);
FImage=fftshift(fft2(double(Image)));  %傅里叶变换及频谱搬移
[N M]=size(FImage);
g=zeros(N,M);
r1=floor(M/2);  r2=floor(N/2);
%figure;
%imshow(log(abs(FImage)+1),[]),title('傅里叶频谱');
d0=[5 30];
d1=[45 70];

for i=1:2
    for x=1:M
        for y=1:N
            d=sqrt((x-r1)^2+(y-r2)^2);
            
            if d>d1  
                h=0;
            else
                if d>d0
                    h=(d-d1)/(d0-d1);
                else
                    h=1;
                end
            end            
            g(y,x)=h*FImage(y,x);
        end
    end
    g=ifftshift(g);
    g=real(ifft2(g));
    figure,imshow(uint8(g)),title(['梯度低通滤波D0=',num2str(d0(i)),',D1=',num2str(d1(i))]);
end

Python实现：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并添加高斯噪声
Image = cv2.imread('lena.bmp', cv2.IMREAD_GRAYSCALE)
Image = cv2.GaussianBlur(Image, (5, 5), 0)
Image = cv2.addWeighted(Image, 1.5, np.zeros(Image.shape, Image.dtype), 0, -0.5)

# 显示原始图像
plt.imshow(Image, cmap='gray')
plt.title('Original Image')
plt.show()

# 进行傅里叶变换及频谱搬移
FImage = np.fft.fftshift(np.fft.fft2(Image.astype(np.float64)))

# 获取图像尺寸
N, M = FImage.shape

# 初始化梯度低通滤波器参数
g = np.zeros((N, M), dtype=np.complex64)
r1 = int(M / 2)
r2 = int(N / 2)
d0 = [5, 30]
d1 = [45, 70]

# 循环处理两组参数
for i in range(2):
    # 计算滤波器系数
    for x in range(M):
        for y in range(N):
            d = np.sqrt((x - r1)**2 + (y - r2)**2)
            
            if d > d1[i]:
                h = 0
            else:
                if d > d0[i]:
                    h = (d - d1[i]) / (d0[i] - d1[i])
                else:
                    h = 1
                    
            g[y, x] = h * FImage[y, x]
    
    # 进行傅里叶逆变换并显示结果
    g = np.fft.ifftshift(g)
    g = np.real(np.fft.ifft2(g))
    plt.imshow(g, cmap='gray')
    plt.title(f'梯度低通滤波D0={d0[i]},D1={d1[i]}')
    plt.show()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/455509.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Day1_vue集成elementUI主体布局

Day1_vue集成elementUI主体布局

本次&#xff0c;将从0开始带你手撸一套SpringBootVue后台管理系统 从前端到后端&#xff0c;手把手搭建&#xff0c;方便学习从0学会基础实战&#xff01;&#xff01;&#xff01; 目录 软件版本 前端开发环境安装&#xff1a; vue-cli安装 : npm设置淘宝镜像加速: 创建v…
阅读更多...
vue2+vue3——1~35

vue2+vue3——1~35

vue2vue3 尚硅谷vue2vue2 课程简介【02:24】vue2 Vue简介【17:59】vue2 Vue官网使用指南【14:07】vue2 搭建Vue开发环境【13:54】vue2 Hello小案例【22:25】了解&#xff1a; 不常用常用&#xff1a;id 更常用 简单class 差值总结vue 实例vue 模板 &#xff1a; 先 取 &#xf…
阅读更多...
【香橙派+DHT11】香橙派（全志H616）+ DHT11温湿度传感器的驱动教程

【香橙派+DHT11】香橙派（全志H616）+ DHT11温湿度传感器的驱动教程

目录 一、前言产品概述特点数据传送逻辑DHT11通信时序 二、代码GPIO初始化起始信号读取数据整体代码执行结果 一、前言 最近写DHT11的代码到香橙派&#xff08;全志H616&#xff09;上&#xff0c;发现网上案例基本上都是树莓派DHT11的居多&#xff0c;香橙派的少&#xff0c;…
阅读更多...
Linux进程通信：无名管道

Linux进程通信：无名管道

进程通信目的&#xff1a; &#xff08;1&#xff09;数据传输&#xff1a;进程间数据传输&#xff1b; &#xff08;2&#xff09;通知事件&#xff1a;一个进程向另一个或一组进程发送消息&#xff0c;通知某个事件的发生&#xff08;如子进程终止时需通知父进程&#xff0…
阅读更多...
使用Lim测试平台快速完成批量造数

使用Lim测试平台快速完成批量造数

一、前言 在我们平时的测试过程中&#xff0c;经常遇到需要造大量数据的情况&#xff0c;比如&#xff1a;测试分页功能&#xff0c;性能压测、数据准备等。 这时我们可以通过写脚本或jmeter这类的工具来实现&#xff0c;但这些方式在团队协作的时候并不友好&#xff0c;当别人…
阅读更多...
MySQL 函数和运算符

MySQL 函数和运算符

文章目录 一、MySQL 函数二、MySQL 运算符总结 一、MySQL 函数 MySQL 有很多内置的函数&#xff0c;以下列出了这些函数的说明。 二、MySQL 运算符 算术运算符 比较运算符 逻辑运算符 位运算符算术运算符 MySQL 支持的算术运算符包括: 除法运算和模运算中&#xf…
阅读更多...
（2）elasticsearch环境搭建(win10)

（2）elasticsearch环境搭建(win10)

安装jdk 版本选择&#xff1a;最好是java 8、java11或者java14 jdk兼容性&#xff1a;https://www.elastic.co/cn/support/matrix#matrix_jvm 操作系统兼容性&#xff1a;https://www.elastic.co/cn/support/matrix 自身兼容性&#xff1a;https://www.elastic.co/cn/suppo…
阅读更多...
Linux下版本控制器(SVN) -服务器端环境搭建步骤

Linux下版本控制器(SVN) -服务器端环境搭建步骤

文章目录 进阶知识-Linux下版本控制器(SVN)4、服务器端环境搭建步骤4.1 安装服务器端程序4.2 验证是否安装成功4.3 创建并配置版本库4.4 配置 SVN对应的服务4.5 启动 SVN服务 本人其他相关文章链接 进阶知识-Linux下版本控制器(SVN) 4、服务器端环境搭建步骤 4.1 安装服务器端…
阅读更多...
AD7356_SPI驱动程序设计_5MSPS_Verilog

AD7356_SPI驱动程序设计_5MSPS_Verilog

好久没动手了&#xff0c;使用Verilog编写一个AD7356的SPI驱动程序。 AD7356是一个双通道、12位、低功耗的ADC。最高采样速率可达5MSPS&#xff0c;全功率输入带宽为110MHz。AD7356的引脚图如下。 SPI的时序图如下&#xff0c;为了使单通道的采样速率达到最高的5MSPS&#xff…
阅读更多...
mac m1的docker nacos2.0.3访问宿主机器的mysql

mac m1的docker nacos2.0.3访问宿主机器的mysql

一、环境介绍&#xff1a; 我的mac系统&#xff1a;m1芯片 macOs Ventura 13.1 我的docker版本&#xff1a;v20.10.8 本机msyql&#xff1a;8.0.25 端口&#xff1a;3306。 mysql版本查询脚本&#xff1a;select version() from dual; 二、准备安装nacos2.0.3 m1版本的镜像 …
阅读更多...
Vue+Echarts 项目演练（中）后台数据接口的创建

Vue+Echarts 项目演练（中）后台数据接口的创建

全局引用Echarts与axios 后台接口创建express路由 api接口数据创建 全局引用Echarts与axios vue3.0的挂载方式&#xff1a;使用Provide/Inject依赖注入&#xff0c;将替代vue2中在原型链上挂载一些属性在app.vue中使用provider来给后代们提供数据 <script> import { p…
阅读更多...
组态王与FX3U之间无线通讯（485BD口）

组态王与FX3U之间无线通讯（485BD口）

设备与设备之间互相通信&#xff0c;需要一座桥梁把二者连接起来&#xff0c;那就是传输通路与通信协议。 传输通路由传输介质与传输接口组成&#xff0c;传输介质可分为有线和无线传输介质两大类。传输接口即通信模块。传输接口常见的有三种RS-232、RS-485和RS-422通信模块。…
阅读更多...
干货|英国专利申请

干货|英国专利申请

英国是世界上公认的一个实施现代专利制度的国家。英国1624年颁布的《垄断法案》被认为是世界上一部具有现代意义的专利法&#xff0c;并成为现代专利保护制度系的起点。英国现行的专利法于1977年颁布&#xff0c;并于1978年生效。英国的专利制度在保护发明创造&#xff0c;促进…
阅读更多...
21.Java网络通信

21.Java网络通信

目录 1. Java基本介绍 2. JDK下载安装及其环境配置 3. 一个简单的java程序 4. Eclipse基本使用、数据类型、运算符 5. 控制语句&#xff08;if、switch、for、while、foreach&#xff09; 6. Java数组 7. Java字符串对象(String|StringBuffer|StringBuilder|StringJoiner…
阅读更多...
Asp.NET CORE实验室信息管理系统源码，支持LIS独立部署，Docker部署

Asp.NET CORE实验室信息管理系统源码，支持LIS独立部署，Docker部署

技术架构&#xff1a;Asp.NET CORE 3.1 MVC SQLserver Redis等 基于B/S架构的实验室管理系统源码&#xff0c;整个系统的运行基于WEB层面&#xff0c;只需要在对应的工作台安装一个浏览器软件有外网即可访问。全套系统采用云部署模式&#xff0c;部署一套可支持多家医院检验科…
阅读更多...
Java ---Object根类

Java ---Object根类

(一&#xff09;定义 官方说法&#xff1a; 在Java中&#xff0c; Object 类是所有类的父类&#xff0c;即Java 的所有类都继承了 Object&#xff0c;子类可以使用 Object 的所有方法。 注意&#xff1a; Object类型的变量与除Object以外的任意引用数据类型的对象都多态引用 所…
阅读更多...
youdiancms 9.5.0 版本 SQL注入（vulfocus复现）

youdiancms 9.5.0 版本 SQL注入（vulfocus复现）

启动服务 从上述信息&#xff0c;可以看到&#xff0c;web服务的80端口被映射到62461端口&#xff0c;并且该服务对外开启了3306端口并映射到20130 端口。并且给了数据库的相关信息。 配置web数据库 登陆后台&#xff0c;后台如下&#xff1a; 探测注入点 上述提到注入点是M…
阅读更多...
OpenGL教程之 纹理练习

OpenGL教程之 纹理练习

网址 LearnOpenGL 练习一 修改片段着色器&#xff0c;仅让笑脸图案朝另一个方向看。  解析&#xff1a;朝向另一个方向很简单&#xff0c;即让上文中的图片进行左右对称变换即可&#xff0c;即将片段着色器中笑脸的纹理坐标从textCord转换为vec2( 1 - textCord.x, text.y …
阅读更多...
【淘宝】商品列表页数据采集+商品销量数据采集代码

【淘宝】商品列表页数据采集+商品销量数据采集代码

采集场景 在淘宝首页&#xff08;https://s.taobao.com/&#xff09;输入关键词搜索&#xff0c;采集搜索后得到的商品列表页数据。示例中关键词为【耐克】&#xff0c;可根据需求进行更换&#xff0c;同时支持自动批量输入多个关键词。 采集字段 采集字段包括关键字文本值…
阅读更多...
Nginx和tomcat反向代理（动静分离）

Nginx和tomcat反向代理（动静分离）

正向代理&#xff1a; 当用户想访问某一网址时&#xff0c;用户先访问代理服务器&#xff0c;然后由代理服务器向目标网址发送请求最终将数据返回代理服务器&#xff0c;最后代理服务器将数据返回给用户这一过程我们称之为正向代理。 反向代理&#xff1a;基本流程是与正向代理…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023