冒泡排序介绍

它是一种较简单的排序算法。它会遍历若干次要排序的数列，每次遍历时，它都会从前往后依次的比较相邻两个数的大小；如果前者比后者大，则交换它们的位置。这样，一次遍历之后，最大的元素就在数列的末尾！采用相同的方法再次遍历时，第二大的元素就被排列在最大元素之前。重复此操作，直到整个数列都有序为止！

冒泡排序实现

下面以数列{20,40,30,10,60,50}为例，演示它的冒泡排序过程(如下图)。

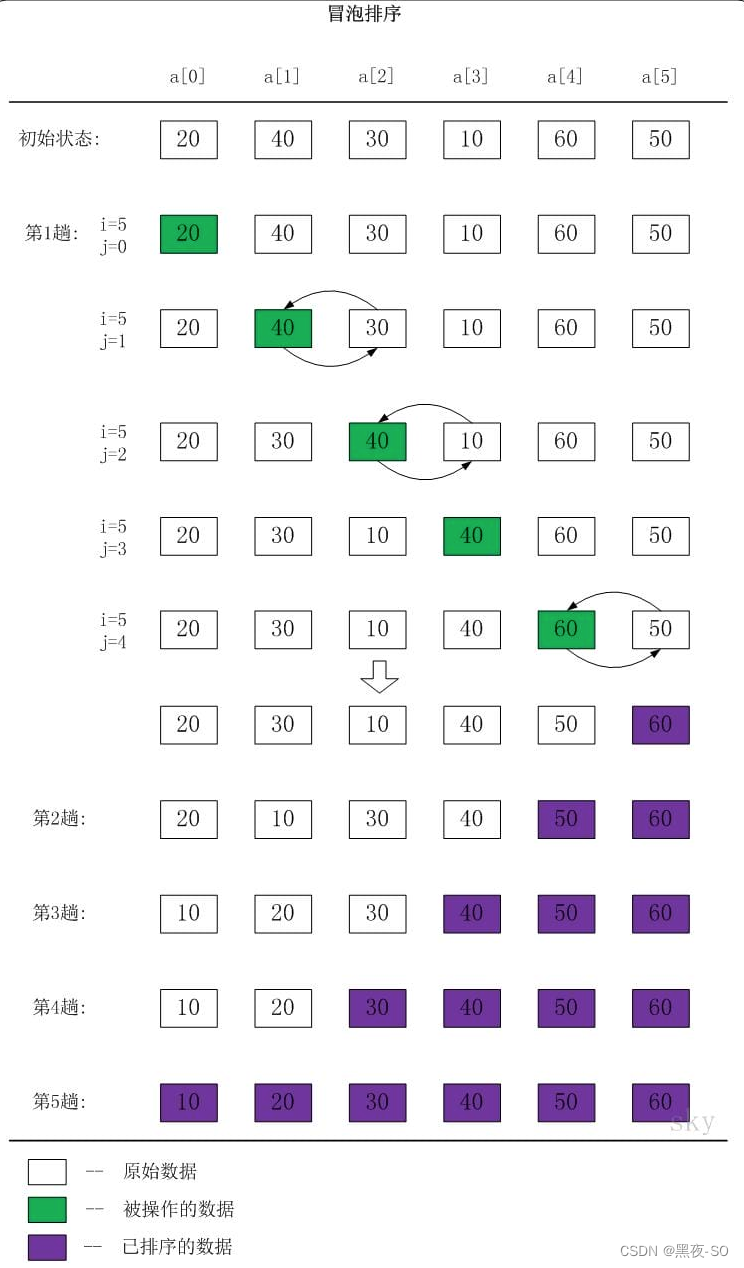
在这里插入图片描述

我们先分析第1趟排序

当i=5,j=0时，a[0]<a[1]。此时，不做任何处理！
当i=5,j=1时，a[1]>a[2]。此时，交换a[1]和a[2]的值；交换之后，a[1]=30，a[2]=40。
当i=5,j=2时，a[2]>a[3]。此时，交换a[2]和a[3]的值；交换之后，a[2]=10，a[3]=40。
当i=5,j=3时，a[3]<a[4]。此时，不做任何处理！
当i=5,j=4时，a[4]>a[5]。此时，交换a[4]和a[5]的值；交换之后，a[4]=50，a[3]=60。

于是，第1趟排序完之后，数列{20,40,30,10,60,50}变成了{20,30,10,40,50,60}。此时，数列末尾的值最大。

根据这种方法:

第2趟排序完之后，数列中a[5…6]是有序的。
第3趟排序完之后，数列中a[4…6]是有序的。
第4趟排序完之后，数列中a[3…6]是有序的。
第5趟排序完之后，数列中a[1…6]是有序的。整个数列也就是有序的了。

复杂度和稳定性

冒泡排序时间复杂度

冒泡排序的时间复杂度是O(N2)。假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? N-1次！因此，冒泡排序的时间复杂度是O(N2)。

冒泡排序稳定性

冒泡排序是稳定的算法，它满足稳定算法的定义。算法稳定性 – 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现


package com.zxn.test;

/**
 * @author zxn
 * @ClassName BubbleSort
 * @Description
 * @createTime 2023年04月24日 01:01:00
 */
public class BubbleSort {
    public static void main(String[] args) {
        int[] a ={30,22,13,4,5,6,7,8,1};
        bubbleSort1(a);
    }

   // 1.0版本
    public static void bubbleSort1(int[] a) {
        int a1,a2;
        for (int i = a.length-1; i >1 ; i--) {
            for (int j = 0; j < i; j++) {
                 a1 = a[j];
                 a2 = a[j + 1];
                 if (a2>a1){
                     int temp = a2;
                     a2 = a1;
                     a1 = temp;
                 }

            }
        }
    }

    // 2.0版本
    public static void bubbleSort2(int[] a) {
        boolean flag =false;
        int a1,a2;
        for (int i = a.length-1; i >1 ; i--) {
            for (int j = 0; j < i; j++) {
                a1 = a[j];
                a2 = a[j + 1];
                if (a2>a1){
                    int temp = a2;
                    a2 = a1;
                    a1 = temp;
                    flag = true;
                }

            }
            if (!flag){
                break;
            }
        }
    }
}