🧑‍💻作者：程序猿爱打拳，Java领域新星创作者，阿里云社区博客专家。

🗃️文章收录于：数据结构与算法

🗂️JavaSE的学习：JavaSE

🗂️MySQL数据库的学习: MySQL数据库

---

在学习数据结构过程中，我们难免会遇到二叉搜索树。网上已经有大量的关于二叉树的博文讲解，但只有少量博文以一步步写代码的形式进行讲解，学起来非常困难。因此，我把二叉搜索树的遍历方式、查找节点、插入节点、删除节点通过图片和文字以及代码的形式一步步展示给大家。

目录

1. 二叉搜索树的概念

2. 二叉搜索树的操作

2.1 查找节点

2.2 插入节点

2.3 删除结点

1. 二叉搜索树的概念

二叉搜索树又称为二叉排序树，它的特点为左子树往后的所有结点都比根节点小，右子树往后的所有结点都比根节点大。根据下图来理解：

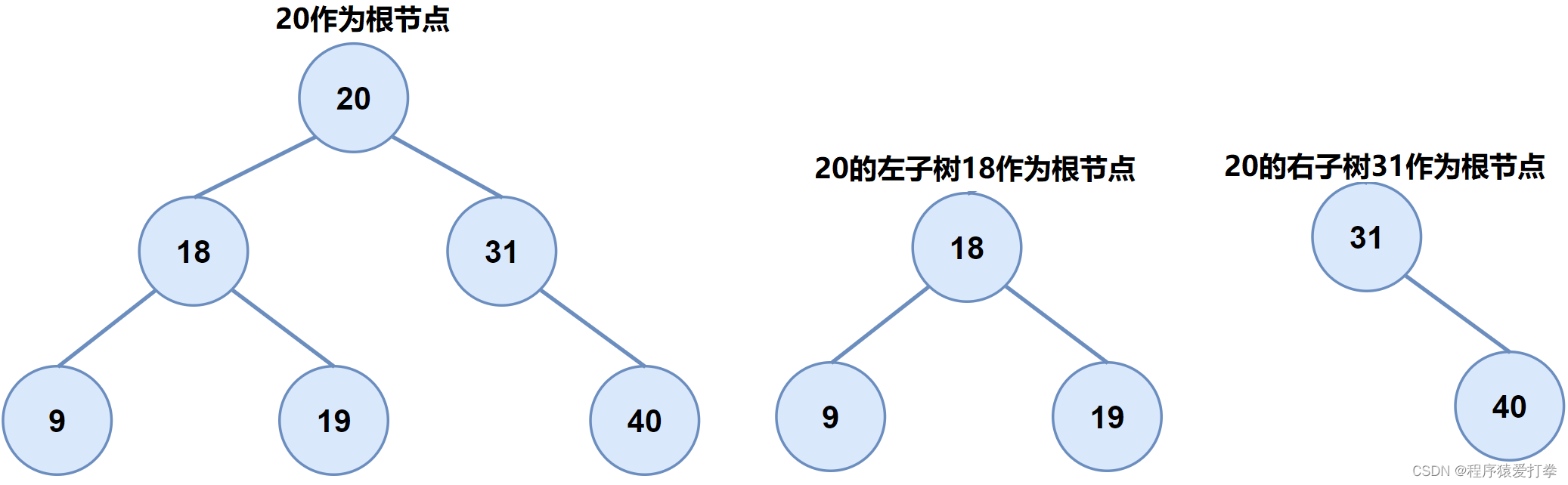
通过上图我们可以观察到，以20为根节点时左侧的所有节点都比20要小，右侧的所有节点都要比20要大。当以20的左子树18、右子树31作为根节点时也是左边节点比根节点小，右边节点比根节点大。

那么以这种结构组成的二叉树，我们就叫做二叉搜索树。因此我们能得出这些性质：

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

首先我们要知道，一个节点是由左子树，值，右子树组成，通常左子树用 left 表示，值用 val 表示，右子树用 right 表示。把三个部分综合起来这样就形成了一个节点，树的根节点用 root 表示因此我们可以定义一个静态内部类 TreeNode 来搭建这个节点：

    //节点结构
    static class TreeNode {
        public TreeNode left;//左子树
        public TreeNode right;//右子树
        public int val;//值

        public TreeNode(int val) {
            this.val = val;//构造方法为成员变量赋值
        }
    }
    public TreeNode root;//根节点

这样节点的搭建就完成了，我们可以看到这个节点内包含的 left、val、right 这三个代表量。 下面，我们就来讲解二叉搜索树的操作：查找节点、插入节点、删除节点。

---

2. 二叉搜索树的操作

2.1 查找节点

查找二叉树的节点，我们根据二叉搜索树的性质下可以列出以下几个条件，

1. 若根节点不为空
2. 根节点等于要查找的节点，返回根节点
3. 根节点大于要查找的节点，在根节点的左子树查找
4. 根节点小于要查找的节点，在根节点的右子树查找
5. 否则，返回null

---

(1).根节点为空

根节点为空代表这个树是不存在的，因此我们直接返回null即可：

    if(root == null) {
        return null;//根节点为空
    }

---

(2).根节点等于要查找的节点

根节点等于要查找的节点我们直接返回根节点即可，这种情况相当于一下子就找到了。因此它的时间复杂度为O(1)。

因此，我们可以写出这样的代码：

    if(root.val == key) {
        return root;//根节点等于要查找的值
    } 
 

root.val 是 root 节点值，key 是我们要查找的数据。注意，我们写代码是一步一步来写的，能实现当前的模块，就写当前的代码。最后综合起来并进行修改这样就能写出一段完整的代码。

---

(3).根节点大于要查找的节点，在根节点的左子树查找

根节点大于要查找的节点，为了满足二叉搜索树的左子树小于根节点的性质，我们要在根节点的左子树进行查找。

 因此，我们可以写出以下代码：

    if(root.val > key) {
        root = root.left; //被查找的值小于根节点
    }

如果 root.val 大于我们要查找的值key，使根节点变为 root 的 left 节点。

---

(4).根节点小于要查找的节点

根节点小于要查找的节点，为了满足二叉搜索树的右子树大于根节点的性质，在根节点的右子树查找。

因此，我们可以写出以下代码:

    if(root.val < key) {
        root = root.right;//被查找的值大于根节点
    }

把以上所有的代码综合起来，这样我们就能写出查找结点的方法。我把查找的结点的方法名命为 findNode，方法内的代码根据上方代码进行修改而成。

方法内的流程为：1.判断节点是否为空，为空则返回null。2.在根节点不为空的情况下，判断要查找的节点是否为根节点是则返回根节点，否则判断该节点在根节点的左子树还是右子树，是左子树就把根节点置为左子树，是右子树就把根节点置为右子树。3.没有该节点，返回null。

public class BinarySearchTree {

    //节点结构
    static class TreeNode {
        public TreeNode left;//左子树
        public TreeNode right;//右子树
        public int val;//值

        public TreeNode(int val) {
            this.val = val;//构造方法获取val的值
        }
    }

    //根节点
    public TreeNode root;

    //查找节点
    public TreeNode findNode(int key) {
        TreeNode node = root; //使node为根节点的一个代替
        if (node == null) { //根节点不为空
            return null;
        }
        while (node != null) { //根节点不为空
            if (node.val == key) { 
                return node;//找到根节点就返回node
            }else if (node.val > key) {
                node = node.left;//根节点的值大于查找的值
            }else {
                node = node.right;//根节点的值小于查找的值
            }
        }
        return null;//没有该节点返回null
    }
}

注意，我们直接使用根节点 root 进行操作的话会改变 root 的位置，这样在其他方法使用 root 结点时不能从最初的根节点(最顶层的根据)进行操作，因此我们可以创建一个代替根节点的代替值 node 来进行操作，这样无论如何 root 始终是在最初的根节点。

---

2.2 插入节点

插入节点，在满足二叉搜索树的性质情况下我们可以列出以下几种情况：

1. 如果树是空树，则之间插入即可。
2. 如果树不是空树，查找顺序确定插入的位置从而插入新节点。

(1)树是空树

我们直接插入一个新节点:

    if(root == null) {
        TreeNode node = new TreeNode(key);//新节点node
        root == node;//把新节点node赋值给root
        return;//结束程序
    }

以上代码中，key是我们要插入的值，因此我们要new一个新节点node来存放key值。然后直接将新节点node赋值给根节点root即可。

---

(2)树不是空树

按照顺序查找可以插入的位置，插入新节点。插入前的查找插入位置，跟上方的 findNode 方法是一样的，因此我们需要了解到的思想是如何进行插入这个环节。

在插入节点的操作时，我们要用一个 parent 来代表根节点的双亲结点，因为当根节点往后遍历走到空时我们无法确认要插入到哪个位置，这时可以使用 parent 这个结点作为根节点来插入新节点。

    TreeNode parent = root;//根节点的双亲结点
    TreeNode cur = root; //根节点的代表结点

当然，我们得使用一个根节点的代表结点 cur 来进行遍历。如何判断插入的位置是 parent 的左子树还是右子树呢？我们可以通过 parent 的 val 值与被插入值 key 进行比较，如果 key 小于 parent 的 val 值则插入到 parent 的左子树否则插入到右子树。因此，我们可以写出以下代码：

    TreeNode node = new TreeNode(key);//创建一个新结点node存放key值
    if(parent.val < key) {
        parent.right = node;//key值大于parent的val值，放在右子树
    }else {
        parent.left = node;//否则放在左子树
    }

---

把上述所有的代码综合起来，我们就能组成以下完整的代码。插入节点的方法名我定义为insertNode，当然你也可以根据自己的设计思想设定方法名以及变量名。

方法内的流程为：1.判断树是否为空，为空直接把插入的结点赋值给根节点。2.找到要插入的位置。3.插入到相应的位置。

 //插入节点
    public void insertNode(int val) {
        if (root == null) {
            root = new TreeNode(key);//新节点就是val值所在的节点
            return;//结束程序
        }
        TreeNode cur = root;//一个cur代替root根节点
        TreeNode parent = null;//根节点的上一个节点
        while(cur != null) {
            if (cur.val == key) {
                return;//如果这个节点存在直接结束程序
            }else if (cur.val > key) {
                parent = cur;
                cur = cur.left;//这个值小于根节点则往左子树走
            }else {
                parent = cur;
                cur = cur.right;//这个值大于根节点则往右子树走
            }
        }
        TreeNode node = new TreeNode(key);//使key值成为一个节点
        if (key > parent.val) {
            parent.right = node;//如果key值大于根节点值则把key值所在节点放在根节点右子树
        }else {
            parent.left = node;//否则放在左子树
        }
    }
}

---

2.3 删除结点

删除二叉搜索树的结点，我们必需在删除该结点后保证这个二叉树还是为二叉搜索树，因此这样的操作是比较难的。

二叉搜索树的难点(重点)就在于删除节点，我们可以设根节点为 root 待删除的节点为 cur，待删除的节点的双亲结点为 parent。因此会出以下情况：

1. cur.left为null时
2. cur.right为null时
3. cur.left不为空并且cur.right不为空时:

---

(1).cur.left为null

当cur.left为null时分为3种情况：

情况1，cur 是 root 时，需要将root=cur.right。

    if (cur.left == null) {
        if (cur == root) {
            root = cur.right;
        }
    }

---

情况2，cur不是root，cur是parent.left时，我们需要将parent.left = cur.right。

    if (cur.left == null) {
        if (cur == parent.left) {
            parent.left = cur.right;
        }
    }

---

情况3，cur不是root，cur是parent.right，我们需要将parent.right = cur.right。

    if (cur.left == null) {
        if (cur == parent.right) {
            parent.right = cur.right;
        }
    }

因此把cur.left为null的三种情况综合起来:

            if (cur.left == null) {
                if (cur == root) {
                    root = cur.right;
                }else if(cur == parent.left) {
                    parent.left = cur.right;
                }else {
                    parent.right = cur.right;
                }
             }

---

(2).cur.right为null

cur.right为null，也分为3种情况：

情况1，cur是root，root=cur.left

    if(cur.right == null) {
        if(cur == root) {
            root = cur.left;
        }
    }

---

情况2，cur不是root，cur是parent.left，parent.left = cur.left

    if(cur.right == null) {
        if(cur == parent.left) {
            parent.left = cur.left;
        }
    }

---

情况3，cur不是root，cur是parent.right，parent.right = cur.left

    if(cur.right == null) {
        if(cur == parent.right) {
            parent.right = cur.left;
        }
    }

把cur.right = null的三种情况综合起来，就能写出以下代码:

            if(cur.right == null) {
                if (cur == root) {
                    root = cur.left;
                }else if(cur == parent.left) {
                    parent.left = cur.left;
                }else {
                    parent.right = cur.left;
                }
             }

---

(3).cur.left不为空且cur.right不为空

当删除的结点左右子树都不为空的情况下，我们就得使用“替换法”来替换被删节点，被替换的节点为被删除节点的右子树的左侧子树的最后一个左子树是最适合用来替换被删节点的，无论哪种情况都是这样，大家可以自行画图测试一下。

目前我们知道了 cur 为要删除的结点，因此替换的结点我们设为 target ，替换节点的双亲结点为 targetParent ，设置替换节点双亲结点是为了当替换节点为空时，我们能找到替换节点！由于是从cur的右子树开始往下遍历，把 target = cur.right ，targetParent = cur。

---

当 cur.right 的最左子树为 target 时：

程序的结束条件为：target.left != null ，直接将该树的值赋值给cur的值即 cur.val = target.val。替换节点删除操作为：targetParent.left = target.right。

---

cur.right 的最左侧不为 target 时：

程序的结束条件为：target.left != null ，直接将该树的值赋值给cur的值即 cur.val = target.val。替换节点删除操作为：targetParent.right = target.right。

 因此，综合上方把cur.left不为空且cur.right不为空可以写成以下代码:

TreeNode target = cur.right;
TreeNode targetParent = cur;
    while (target.left != null) {//终止条件为最左侧为空
        targetParent = target;
        target = target.left;
    }
        cur.val = target.val;//把cur的值替换为target的值
        if (target == targetParent.left) {
                targetParent.left = target.right;//最左侧值等于target
        }else {
                targetParent.right = target.right;//最左侧值不等于target
        }

---

把删除节点中所有代码综合起来，我们就能写出完整的删除操作。当然，我们得先找到删除的节点又使用到了 findNode 的操作，我把删除节点的操作封装到一个名为 removeNode 的方法里面，以下为完整代码:

//查找节点
    public void delNode(int key) {
        TreeNode cur = root;
        TreeNode parent = null;
        while(cur != null) {
            if (cur.val == key) {
                removeNode(cur,parent);//调用删除节点方法
            }else if(cur.val > key) {
                parent = cur;
                cur = cur.left;
                removeNode(cur,parent);//调用删除节点方法
            }else {
                parent = cur;
                cur = cur.right;
                removeNode(cur,parent);//调用删除节点方法
            }
        }
    }

    //删除节点
    public void removeNode(TreeNode parent,TreeNode cur) {
        while (cur != null) {
            if (cur.left == null) {
                if (cur == root) {
                    root = cur.right;
                }else if(cur == parent.left) {
                    parent.left = cur.right;
                }else {
                    parent.right = cur.right;
                }
            }else if(cur.right == null) {
                if (cur == root) {
                    root = cur.left;
                }else if(cur == parent.left) {
                    parent.left = cur.left;
                }else {
                    parent.right = cur.left;
                }
            }else{
                TreeNode target = cur.right;
                TreeNode targetParent = cur;
                while (target.left != null) {
                    targetParent = target;
                    target = target.left;
                }
                cur.val = target.val;
                if (target == targetParent.left) {
                    targetParent.left = target.right;
                }else {
                    targetParent.right = target.right;
                }
            }

        }
    }

---

🧑‍💻作者：程序猿爱打拳，Java领域新星创作者，阿里云社区博客专家。

🗃️文章收录于：数据结构与算法

🗂️JavaSE的学习：JavaSE

🗂️MySQL数据库的学习: MySQL数据库

本片博文到这里就结束了，感谢各位的阅读。

​