11. 图的入门

news2024/10/6 10:41:53

11. 图的入门

11.1 图的实际应用：

​ 在现实生活中，有许多应用场景会包含很多点以及点点之间的连接，而这些应用场景我们都可以用即将要学习的图这种数据结构去解决。

地图：

​ 我们生活中经常使用的地图，基本上是由城市以及连接城市的道路组成，如果我们把城市看做是一个一个的点，把道路看做是一条一条的连接，那么地图就是我们将要学习的图这种数据结构。

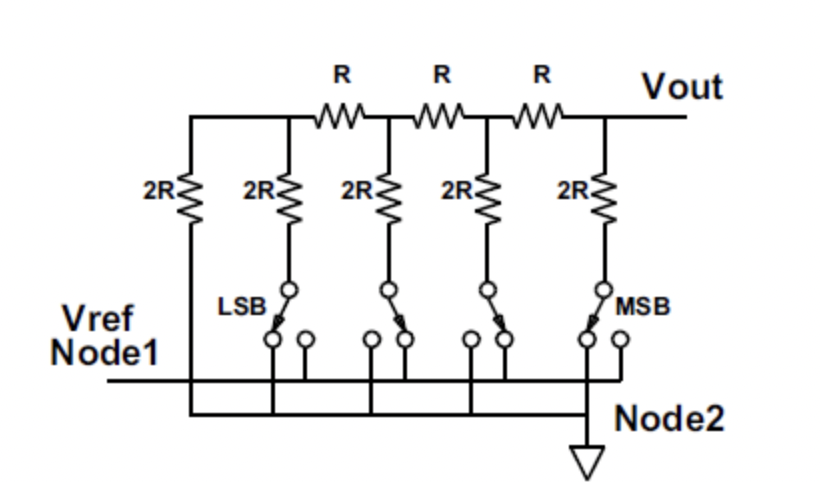
电路图：

​ 下面是一个我们生活中经常见到的集成电路板，它其实就是由一个一个触点组成，并把触点与触点之间通过线进行连接，这也是我们即将要学习的图这种数据结构的应用场景。

11.2 图的定义及分类

**定义：**图是由一组顶点和一组能够将两个顶点相连的边组成的

特殊的图：

  1. 自环：即一条连接一个顶点和其自身的边；

  2. 平行边：连接同一对顶点的两条边；

图的分类：

按照连接两个顶点的边的不同，可以把图分为以下两种：

无向图：边仅仅连接两个顶点，没有其他含义；

有向图：边不仅连接两个顶点，并且具有方向；

11.3 无向图

11.3.1 图的相关术语

相邻顶点：

当两个顶点通过一条边相连时，我们称这两个顶点是相邻的，并且称这条边依附于这两个顶点。

度：

某个顶点的度就是依附于该顶点的边的个数。

子图：

是一幅图的所有边的子集(包含这些边依附的顶点)组成的图；

路径：

是由边顺序连接的一系列的顶点组成

环：

是一条至少含有一条边且终点和起点相同的路径

连通图：

如果图中任意一个顶点都存在一条路径到达另外一个顶点，那么这幅图就称之为连通图

连通子图：

一个非连通图由若干连通的部分组成，每一个连通的部分都可以称为该图的连通子图

11.3.2 图的存储结构

要表示一幅图，只需要表示清楚以下两部分内容即可：

  1. 图中所有的顶点；

  2. 所有连接顶点的边；

常见的图的存储结构有两种：邻接矩阵和邻接表

11.3.2.1 邻接矩阵

  1. 使用一个V*V的二维数组int[V][V] adj,把索引的值看做是顶点；

  2. 如果顶点v和顶点w相连，我们只需要将adj[v][w]和adj[w][v]的值设置为1,否则设置为0即可。

很明显，邻接矩阵这种存储方式的空间复杂度是V^2的，如果我们处理的问题规模比较大的话，内存空间极有可能不够用。

11.3.2.2 邻接表

  1. 使用一个大小为V的队列数组 Queue[V] adj，把索引看做是顶点；

  2. 每个索引处adj[v]存储了一个队列，该队列中存储的是所有与该顶点相邻的其他顶点。

很明显，邻接表的空间是线性级别的，所以后面我们一直采用邻接表这种存储形式来表示图。

11.3.3 图的实现(邻接表实现)

11.3.3.1 图的API设计

package com.ynu.Java版算法.U11_图的入门.T1_无向图.S1_图的实现;

import java.util.LinkedList;
import java.util.Queue;

public class Graph {

    // 顶点数目
    private final int V;
    // 边的数目
    private int E;
    // 邻接表
    private Queue<Integer>[] adj;

    public Graph(int v) {
        // 初始化顶点的数量
        this.V = v;
        // 初始化边的数量
        E = 0;
        // 初始化邻接表
        adj = new Queue[V];
        for (int i = 0; i < adj.length; i++) {
            adj[i] = new LinkedList<Integer>();
        }

    }


    //获取顶点数目
    public int getV(){
        return V;
    }

    //获取边的数目
    public int getE(){
        return E;
    }

    // 向图中添加一条边 v-w 连接v,w顶点
    // v顶点的链表上添加w  w的顶点上添加v
    public void addEdge(int v,int w){
        // 把w添加到v的链表中，这样顶点v就多了一个相邻点w
        adj[v].offer(w);
        //把v添加到w的链表中，这样顶点w就多了一个相邻点v
        adj[w].offer(v);
        //边的数目自增1
        E++;
    }
    
    //获取和顶点v相邻的所有顶点
    public Queue<Integer> adj(int v){
        return adj[v];
    }


}

11.3.4 图的搜索

在很多情况下，我们需要遍历图，得到图的一些性质，例如，找出图中与指定的顶点相连的所有顶点，或者判定某

个顶点与指定顶点是否相通，是非常常见的需求。

有关图的搜索，最经典的算法有深度优先搜索和广度优先搜索，接下来我们分别讲解这两种搜索算法。

11.3.4.1 深度优先搜索(DFS)

所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，然后找

兄弟结点。

package com.ynu.Java版算法.U11_图的入门.T1_无向图.S2_图的搜索.A1_深度优先搜索;

import java.util.LinkedList;
import java.util.Queue;

public class DepthFirstSearch {

    // 标记数组。 索引代表顶点，值表示当前顶点是否已经被搜索过
    private boolean[] marked;

    // 记录有多少个顶点与s顶点相通
    private int count;

    // 记录遍历的结果
    private Queue<Integer> list = new LinkedList<>();

    public DepthFirstSearch(Graph graph) {
        marked = new boolean[graph.V()];
    }

    // 构造深度优先搜索对象，使用深度优先搜索找出G图中与s顶点相通的所有顶点。从s节点开始遍历整个图。
    public DepthFirstSearch(Graph graph,int s) {
        marked = new boolean[graph.V()];
        // 深度优先遍历
        dfs(graph,s);
        // 如果遍历完,marked全部为true。说明是graph是一个连通图
    }

    // 使用深度优先搜索找出G图中与v顶点相通的所有顶点
    public void dfs(Graph graph,int v){

        list.offer(v);
        marked[v] = true;  // v访问过，同时也表明s与v是相通的

        //获取顶点v的领接表
        Queue<Integer> adjV = graph.adj(v);
        //遍历顶点v的领接表，往下搜索    一个节点领接表上的所有节点就算是兄弟节点
        for (Integer w : adjV) {
            if (!marked[w])
                dfs(graph,w);
        }

        // 能连通的节点数加1
        count++;
    }

    // 判断顶点w与顶点s是否相通
    public boolean marked(int w){
        return marked[w];
    }

    // 判断是否是连通图
    public boolean isLianTong(){
        for (boolean b : marked) {
            if (b==false){
                return false;
            }
        }
        return true;
    }

    // 获取遍历结果
    public void printGraph(){
        while (!list.isEmpty()){
            System.out.print(list.peek() + " ");
            marked[list.poll()] = false;
        }
    }

}


package com.ynu.Java版算法.U11_图的入门.T1_无向图.S2_图的搜索.A1_深度优先搜索;

public class Main {
    public static void main(String[] args) {

        // 创建有10个节点的图
        Graph g = new Graph(10);
        g.addEdge(0,1);
        g.addEdge(1,2);
        g.addEdge(2,3);
        g.addEdge(3,4);
        g.addEdge(4,5);
        g.addEdge(5,6);
        g.addEdge(6,7);
        g.addEdge(7,8);
        g.addEdge(8,9);
        g.addEdge(9,1);
        // 输出边的个数   10
        System.out.println(g.E());

        // 从1节点开始遍历图
        DepthFirstSearch depthFirstSearch = new DepthFirstSearch(g);
        depthFirstSearch.dfs(g,0);
        depthFirstSearch.printGraph();

        System.out.println();

        // 从0开始深度遍历图
        depthFirstSearch.dfs(g,0);
        depthFirstSearch.printGraph();

        System.out.println();
        // 从3开始遍历图
        depthFirstSearch.dfs(g,3);
        depthFirstSearch.printGraph();


    }
}
11.3.4.2 广度优先搜索(BFS)

所谓的深度优先搜索，指的是在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后

找子结点。

package com.ynu.Java版算法.U11_图的入门.T1_无向图.S2_图的搜索.A2_广度优先搜索;

import java.util.LinkedList;
import java.util.Queue;

public class BreadthFirthSearch {

    // 标记数组  标记是否遍历过该节点
    private boolean[] marked;

    // 存储结果的队列
    private Queue<Integer> res = new LinkedList<>();

    // 辅助队列:等待遍历的队列。 类似二叉树的层序遍历，需要一个队列就行帮助。
    private Queue<Integer> waitSearch;

    //记录有多少个顶点与s顶点相通
    private int count;

    public BreadthFirthSearch(Graph graph) {
        marked = new boolean[graph.V()];
        waitSearch = new LinkedList<>();
    }

    public BreadthFirthSearch(Graph graph, int s) {
        waitSearch = new LinkedList<>();
        bfs(graph,s);
    }


    public void bfs(Graph graph,int s){

        waitSearch.offer(s);

        while (!waitSearch.isEmpty()){

            Integer w = waitSearch.poll();
            res.offer(w);   // 访问该节点
            marked[w] = true;
            // 获取w的邻接表
            Queue<Integer> adjW = graph.adj(w);
            for (Integer i : adjW) {
                if (!marked[i])
                    waitSearch.offer(i);   // 放进辅助队列
            }
        }
    }
    
    // 判断顶点w与顶点s是否相通
    public boolean marked(int w){
        return marked[w];
    }
    
    // 判断是否是连通图
    public boolean isLianTong(){
        for (boolean b : marked) {
            if (b==false){
                return false;
            }
        }
        return true;
    }


    // 获取遍历结果
    public void printGraph(){
        while (!res.isEmpty()){
            System.out.print(res.peek() + " ");
            marked[res.poll()] = false;
        }
    }


}

11.3.5 案例-畅通工程续1

​ 某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。目前的道路状况，9号城市和10号城市是否相通？9号城市和8号城市是否相通？

下面是对数据的解释：

package com.ynu.Java版算法.U11_图的入门.T1_无向图.S2_图的搜索.畅通工程;

import org.junit.Test;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class Main {


    @Test
    public void test(){
       List<List<Integer>> paths = new ArrayList<>();
        paths.add(Arrays.asList(0,1));  // 连通0,1
        paths.add(Arrays.asList(6,9));
        paths.add(Arrays.asList(3,8));
        paths.add(Arrays.asList(5,11));
        paths.add(Arrays.asList(2,12));
        paths.add(Arrays.asList(6,10));
        paths.add(Arrays.asList(4,8));

        // 9号和10号城市是否相通
        System.out.println(isConnected(20,paths,9,10));
        System.out.println(isConnected1(20,paths,9,10));
        // 9号和8号城市是否相通
        System.out.println(isConnected(20,paths,9,8));
        System.out.println(isConnected1(20,paths,9,8));
        // 5号和11号城市是否相通
        System.out.println(isConnected(20,paths,5,11));
        System.out.println(isConnected1(20,paths,5,11));


    }

    // 1.使用深度优先遍历
    public boolean isConnected(int nums,List<List<Integer>> paths,int i,int j){

        // 构建大小为20的图 表示20个城市   0-19号城市
        Graph graph = new Graph(20);
        boolean[] marked = new boolean[20];

        // 加边
        for (List<Integer> path : paths) {
            Integer v = path.get(0);
            Integer w = path.get(1);
            graph.addEdge(v,w);
        }

        // 深度优先遍历
        // i号城市对应的索引为i-1
        // j城市对应的索引为j-1
        dfs(graph,i,marked);
        return marked[j];
    }

    // 从v节点开始深度优先搜索
    public void dfs(Graph graph,int v,boolean[] marked){

        marked[v] = true;

        // 获取v节点的邻接表
        Queue<Integer> adjV = graph.adj(v);

        for (Integer i : adjV) {
            if (!marked[i]){
                dfs(graph,i,marked);
            }
        }


    }


    // 2.使用广度优先遍历
    public boolean isConnected1(int nums,List<List<Integer>> paths,int i,int j){


        // 构建大小为20的图 表示20个城市   0-19号城市
        Graph graph = new Graph(20);
        boolean[] marked = new boolean[20];

        // 加边
        for (List<Integer> path : paths) {
            Integer v = path.get(0);
            Integer w = path.get(1);
            graph.addEdge(v,w);
        }

        bfs(graph,i,marked);

        return marked[j];
    }

    // 从v节点开始深度优先搜索
    public void bfs(Graph graph,int v,boolean[] marked){

        // 辅助队列
        Queue<Integer> queue = new LinkedList<>();

        queue.offer(v);

        while (!queue.isEmpty()){
            Integer top = queue.poll();
            marked[top] =  true;

            // 获取邻接表
            Queue<Integer> adj = graph.adj(top);
            for (Integer i : adj) {
                if (!marked[i]){
                    queue.offer(i);
                }
            }
        }

    }

}

11.3.6 路径查找

​ 在实际生活中，地图是我们经常使用的一种工具，通常我们会用它进行导航，输入一个出发城市，输入一个目的地城市，就可以把路线规划好，而在规划好的这个路线上，会路过很多中间的城市。这类问题翻译成专业问题就是：

​ 从s顶点到v顶点是否存在一条路径？如果存在，请找出这条路径。

例如在上图上查找顶点0到顶点4的路径用红色标识出来,那么我们可以把该路径表示为 0-2-3-4。

​ 我们实现路径查找，最基本的操作还是得遍历并搜索图，所以，我们的实现暂且基于深度优先搜索来完成。其搜索的过程是比较简单的。我们添加了edgeTo[]整型数组，这个整型数组会记录从每个顶点回到起点s的路径。 如果我们把顶点设定为0，那么它的搜索可以表示为下图：

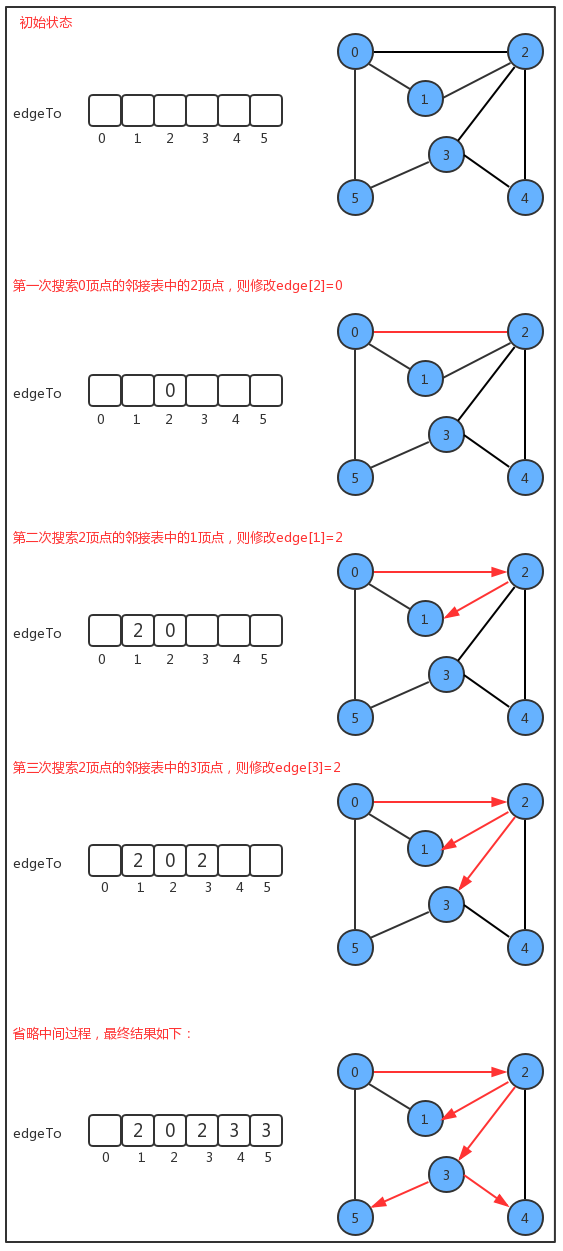
根据最终edgeTo的结果，我们很容易能够找到从起点0到任意顶点的路径； 只不过这个路径是反着的，需要再倒序遍历一下，可以借助栈。

代码：

package com.ynu.Java版算法.U11_图的入门.T1_无向图.S2_图的搜索.A4_路径查找;

import org.junit.Test;

import java.util.*;

public class Main {


    @Test
    public void test(){
        List<List<Integer>> paths = new ArrayList<>();
        paths.add(Arrays.asList(0,2));  // 连通0,1
        paths.add(Arrays.asList(0,1));
        paths.add(Arrays.asList(2,1));
        paths.add(Arrays.asList(2,3));
        paths.add(Arrays.asList(2,4));
        paths.add(Arrays.asList(3,5));
        paths.add(Arrays.asList(3,4));
        paths.add(Arrays.asList(0,5));

        // 从0-5的所有路径
        System.out.println(findPath(6, paths, 0, 5));

        // 从0-5的最短路径
        System.out.println(findPath1(6, paths, 0, 5));

        // 从1-5的所有路径
        System.out.println(findPath(6, paths, 1, 5));
        // 从1-5的最短路径
        System.out.println(findPath1(6, paths, 1, 5));

    }

    // 1.使用深度优先遍历  -- 能查出所有路径
    public List<List<Integer>> findPath(int nums,List<List<Integer>> paths,int i,int j){

        List<List<Integer>> res = new ArrayList<>(); // 所有路径结果
        LinkedList<Integer> tempPath = new LinkedList<>();  // 某一条路径

        // 1. 构建大小为20的图 表示20个城市   0-19号城市
        Graph graph = new Graph(20);
        boolean[] marked = new boolean[20];
        // 加边
        for (List<Integer> path : paths) {
            Integer v = path.get(0);
            Integer w = path.get(1);
            graph.addEdge(v,w);
        }

        // 2.深度优先遍历
        marked[i] = true;
        tempPath.add(i);
        dfs(res,tempPath,graph,i,j,marked);

        return res;
    }

    /**
     *
     * @param res
     * @param path
     * @param graph
     * @param start  起点
     * @param des    终点
     * @param marked
     */
    public void dfs(List<List<Integer>> res,LinkedList<Integer> path,Graph graph, int start, int des,boolean[] marked){
        // 到达目的地
        if (!path.isEmpty() && path.getLast()==des){
            res.add(new LinkedList<>(path));
            return;
        }

        //获取v的邻接表
        Queue<Integer> adjV = graph.adj(start);
        for (Integer j : adjV) {
            if (!marked[j]){
                path.add(j);
                marked[j] = true;
                dfs(res, path, graph, j, des, marked);
                // 回溯
                path.removeLast();
                marked[j] = false;
            }
        }


    }


    // 2.使用广优先遍历  一定是最短路径
    public List<Integer> findPath1(int nums,List<List<Integer>> paths,int start,int des){

        List<Integer> res = new ArrayList<>();
        // 大小为nums的标记数组 记录是否遍历过
        boolean[] marked = new boolean[nums];

        // 构建图
        Graph graph = new Graph(nums);
        for (List<Integer> path : paths) {
            Integer v = path.get(0);
            Integer w = path.get(1);
            graph.addEdge(v,w);
        }

        int[] edgeTo = new int[nums]; // edgeTo[]整型数组，这个整型数组会记录从每个顶点回到起点i的路径。很多地方是写为prev数组
        // 比如edge[j] = i  表示要到j,前一个节点是i
        Arrays.fill(edgeTo,-1);

        bfs(graph,edgeTo,start,des,marked);  // 广度优先遍历

        // 去寻找到des要经过的路径
        int j = des;
        res.add(j);
        while (edgeTo[j]!=-1 && edgeTo[j]!=des){
            res.add(edgeTo[j]);
            j = edgeTo[j];
        }
        //由于寻找是按照反着的顺序来的，所以需要把res倒序过来
        Collections.reverse(res);
        return res;
    }

    public void bfs(Graph graph,int[] edgeTo,int start,int end,boolean[] marked){

        // 辅助队列
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(start);

        while (!queue.isEmpty()){
            Integer top = queue.poll();
            marked[top] = true;

            if (top==end){
                return;
            }

            // 获取邻接表
            Queue<Integer> adjV = graph.adj(top);
            for (int j : adjV) {
                if (!marked[j]){
                    edgeTo[j] = top;
                    queue.offer(j);
                }
            }

        }

    }



}

11.3.7 路径查找——最短路径

在11.3.6遍历的时候使用广度优先遍历

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/451943.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

关于函数栈帧的创建与销毁和可变参数列表

关于函数栈帧的创建与销毁和可变参数列表

目录 1. 深刻理解函数调用过程1.1 基本概念1.2 函数栈帧的创建于销毁1.2.1 栈帧创建1.2.2 栈帧销毁1.2.3 有趣的现象 2. 了解可变参数列表的使用与原理2.1 可变参数列表与函数栈帧的关系2.2 宏的工作过程2.3 宏的具体实现原理 1. 深刻理解函数调用过程 1.1 基本概念 关于函数…
阅读更多...
VBA智慧办公9——图例控件教程

VBA智慧办公9——图例控件教程

如图&#xff0c;利用VBA进行可视化交互界面的设计&#xff0c;在界面中我们用到了label&#xff0c;button&#xff0c;text&#xff0c;title等多个工具&#xff0c;在进行框图效果的逐一实现后可进行相应的操作和效果实现。 VBA&#xff08;Visual Basic for Applications&a…
阅读更多...
家用洗地机要怎么选？平价洗地机推荐

家用洗地机要怎么选？平价洗地机推荐

国内大多数家庭比较注重地面清洁&#xff0c;不仅是要扫的干净&#xff0c;更要拖的干净&#xff0c;尤其追求地板锃亮的视觉效果&#xff0c;因此家用洗地机因其清洁效率高、能吸除干湿垃圾以及自清洁拖布等优点&#xff0c;成为很多家庭用于替代扫帚拖把等传统清洁工具的清洁…
阅读更多...
可视化Echarts 柱状图、饼状图、折线图的设置

可视化Echarts 柱状图、饼状图、折线图的设置

柱状图 饼状图 折线图 柱状图 基本的柱状图设置 <template> <div ref"ec" id"ec"></div> </template><script> import * as echarts from "echarts"; //引用echartsexport default {mounted(){let mc ech…
阅读更多...
【网络安全】CVE 漏洞分析以及复现

【网络安全】CVE 漏洞分析以及复现

漏洞详情 Shiro 在路径控制的时候&#xff0c;未能对传入的 url 编码进行 decode 解码&#xff0c;导致攻击者可以绕过过滤器&#xff0c;访问被过滤的路径。 漏洞影响版本 Shiro 1.0.0-incubating 对应 Maven Repo 里面也有 【一一帮助安全学习&#xff0c;所有资源获取一一…
阅读更多...
onnx手动操作001

onnx手动操作001

使用onnx.helper可以进行onnx的制造组装操作&#xff1a; 对象描述ValueInfoProto 对象张量名、张量的基本数据类型、张量形状算子节点信息 NodeProto算子名称(可选)、算子类型、输入和输出列表(列表元素为数值元素)GraphProto对象用张量节点和算子节点组成的计算图对象ModelP…
阅读更多...
王道计组(23版)3_存储系统

王道计组(23版)3_存储系统

概述 RAM&#xff1a;随机存储器&#xff0c;任一个存储单元可以随机存取&#xff0c;易失。用作主存(DRAM)或Cache(SRAM) ROM&#xff1a;只读存储器&#xff0c;可随机读出&#xff0c;写入较慢&#xff0c;需刷新&#xff0c;非易失。Flash、SSD固态硬盘、U盘 _____SSD&…
阅读更多...
某医院网络安全分析案例

某医院网络安全分析案例

背景 我们已将NetInside流量分析系统部署到某市医院的机房内&#xff0c;使用流量分析系统提供实时和历史原始流量。本次分析重点针对网络流量安全进行分析&#xff0c;以供安全取证、网络质量监测以及深层网络分析。 分析时间 报告分析时间范围为&#xff1a;2023-04-12 16…
阅读更多...
牛客网Verilog刷题——VL3

牛客网Verilog刷题——VL3

牛客网Verilog刷题——VL3 题目答案 题目 要求设计一个奇偶校验模块&#xff0c;根据sel信号选择进行奇校验还是偶校验&#xff08;sel0&#xff0c;进行偶校验&#xff1b;sel1&#xff0c;进行奇校验&#xff09;&#xff0c;根据输入的32位数据生成1位的奇偶校验位。   …
阅读更多...
云安全监控及云数据保护

云安全监控及云数据保护

如今&#xff0c;许多公司已经迁移到云&#xff0c;目的是进行扩展和现代化&#xff0c;但在此过程中&#xff0c;他们面临着新的、代价高昂的风险。云安全是一种多管齐下的方法&#xff0c;专注于保护数据和业务内容&#xff0c;同时确保企业的业务运营高效运行。 监控云访问 …
阅读更多...
JMM 内存模型

JMM 内存模型

文章目录 1、 java 内存模型1.1 原子性1.2 问题分析1.3 解决方法 2、可见性2.1 退不出的循环2.2 解决方法2.3 可见性 3、有序性3.1 诡异的结果3.2 解决方法3.3 有序性理解3.4 happens-before 4、CAS 与 原子类4.1 CAS4.2 乐观锁与悲观锁4.3 原子操作类 5、synchronized 优化5.1…
阅读更多...
MemCache详细解读

MemCache详细解读

目录 一、MemCache是什么 二、MemCache特性和限制 三、MemCache实现原理 四、MemCache的Java实现实例 五、MemCache指令汇总 一、MemCache是什么 MemCache是一个自由、源码开放、高性能、分布式的分布式内存对象缓存系统&#xff0c;用于动态Web应用以减轻数据库的负载。它…
阅读更多...
【李宏毅】自注意力机制self-attention

【李宏毅】自注意力机制self-attention

课件网址&#xff1a; 【機器學習2021】自注意力機制 (Self-attention) (上) - YouTube 【機器學習2021】自注意力機制 (Self-attention) (下) - YouTube 这两章课程主要在讲self-attention是怎么做的&#xff0c;对应的矩阵操作是什么&#xff0c;以及为什么要这样处理。 …
阅读更多...
MySQL_第13章_约束

MySQL_第13章_约束

第13章_约束 1. 约束(constraint)概述 1.1 为什么需要约束 数据完整性&#xff08;Data Integrity&#xff09;是指数据的精确性&#xff08;Accuracy&#xff09;和可靠性&#xff08;Reliability&#xff09;。它是防止数据库中存在不符合语义规定的数据和防止因错误信息…
阅读更多...
SQL Server 意向锁

SQL Server 意向锁

SQL Server 数据库引擎使用意向锁来确保共享锁&#xff08;S 锁&#xff09;或排他锁&#xff08;X 锁&#xff09;放置在锁层次结构的底层资源上。 意向锁之所以命名为意向锁&#xff0c;是因为在较低级别锁前可获取它们&#xff0c;因此会通知意向将锁放置在较低级别上。 意向…
阅读更多...
fastadmin后台用户管理中余额记录显示

fastadmin后台用户管理中余额记录显示

查询明细JS代码 {field: buttons,width: "200px",title: __(查询明细),table: table,events: Table.api.events.operate,buttons: [{name: money,text: __(余额),title: __(余额),classname: btn btn-xs btn-success btn-dialog,icon: fa fa-database,url: user/us…
阅读更多...
按照条件向Spring容器中注册bean

按照条件向Spring容器中注册bean

1.Conditional注解概述 Conditional注解可以按照一定的条件进行判断&#xff0c;满足条件向容器中注册bean&#xff0c;不满足条件就不向容器中注册bean。 package org.springframework.context.annotation;import java.lang.annotation.Documented; import java.lang.annota…
阅读更多...
数据转换器的工程师指南

数据转换器的工程师指南

数据转换是连接模拟和数字世界的重要电路&#xff0c;在大多数嵌入式系统中&#xff0c;您都会发现模拟到数字转换和数字到模拟转换&#xff0c;从物联网&#xff08;IoT&#xff09;传感器到无线网络&#xff0c;从智能家居自动化到电源&#xff0c;数据转换无处不在。在本文中…
阅读更多...
Git在工作中的使用流程

Git在工作中的使用流程

Git中的分支 master分支&#xff1a;所有用户可见的正式版本&#xff0c;都从master发布&#xff08;也是用于部署生产环境的分支&#xff0c;确保master分支稳定性&#xff09;。主分支作为稳定的唯一代码库&#xff0c;不做任何开发使用。master 分支一般由develop以及hotfi…
阅读更多...
自学黑客/网络安全，三个月究竟能学到多少知识？

自学黑客/网络安全，三个月究竟能学到多少知识？

现在可以看到很多标题都是三个月零基础转行网络安全&#xff0c;三个月成为网络安全工程师月入15K&#xff0c;还有很多一系列类似吸引人的标题&#xff0c;那这些话是不是真实情况呢&#xff1f;那我们就来整理一下这三个月可以学到什么&#xff0c;然后再来看根据三个月的学习…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023