文章目录
- 前言
- 一、邻接矩阵
- 1.概念
- 2.图像示例
- 3. 代码实现
- 注意
- 邻接矩阵的特点
- 二、邻接表
- 1.概念
- 2.图像示例
- 3.代码实现
- 邻接表的特点
前言
图是一种比较复杂的数据结构,每个结点之间可以有多种关系。
所以,一个图可以呈现出千奇百怪的形式。
对于不同的形式的图,我们可以用不同的存储方式来进行存储。
比如说:
- 对于边比较少而结点很多的图,我们需要把更多的存储空间用于存放顶点的信息,如果两个顶点之间不存在边,那么就不需要花费存储空间来说明这个地方没有边。
- 对于边比较多而顶点相对没那么多的图,在每一个顶点之间,都很有可能存在边,如果每一条边都单独考虑,会显得比较繁琐。
- 对于插入和删除边的操作做的比较多的图,我们更希望更快的找到这条边的信息在那个位置,于是具有随机存取性质的数据结构更加实用。
像这样的例子还有很多,下面总结一下最常用的两种存储方式——邻接矩阵和邻接表。
一、邻接矩阵
1.概念
所谓邻接矩阵存储,是指用一个一维数组存储图中顶点的信息,用一个二维数组存储图中边的信息(即各顶点之间的邻接关系),存储顶点之间邻接关系的二维数组称为邻接矩阵。
- 顶点数为n的图G的邻接矩阵为 n × n \ n×n n×n的二维数组,如果记顶点编号为v1, v2, …, vn,则对于顶点vi和vj,若存在一条边(vi, vj)∈E,则A[i][j] = 1, 否则A[i][j] = 0,即
A [ i ] [ j ] = { 1 , 若 ( v i , v j ) 或 ⟨ v i , v j ⟩ 是 E ( G ) 中的边 0 , 若 ( v i , v j ) 或 ⟨ v i , v j ⟩ 不是 E ( G ) 中的边 A[i][j]=\left\{\begin{array}{ll} 1, & \text { 若 }\left(v_{i}, v_{j}\right) \text { 或 }\left\langle v_{i}, v_{j}\right\rangle \text { 是 } E(G) \text { 中的边 } \\ 0, & \text { 若 }\left(v_{i}, v_{j}\right) \text { 或 }\left\langle v_{i}, v_{j}\right\rangle \text { 不是 } E(G) \text { 中的边 } \end{array}\right. A[i][j]={1,0, 若 (vi,vj) 或 ⟨vi,vj⟩ 是 E(G) 中的边 若 (vi,vj) 或 ⟨vi,vj⟩ 不是 E(G) 中的边
- 对于带权图而言,若顶点v,和 v;之间有边相连,则邻接矩阵中对应项存放着该边对应的权值,若顶点V和V不相连,则用 ∞ \ \infty ∞来代表这两个顶点之间不存在边:
A [ i ] [ j ] = { w i j , 若 ( v i , v j ) 或 ⟨ v i , v j ⟩ 是 E ( G ) 中的边 0 或 ∞ , 若 ( v i , v j ) 或 ⟨ v i , v j ⟩ 不是 E ( G ) 中的边 A[i][j]=\left\{\begin{array}{ll} w_{i j}, & \text { 若 }\left(v_{i}, v_{j}\right) \text { 或 }\left\langle v_{i}, v_{j}\right\rangle \text { 是 } E(G) \text { 中的边 } \\ 0 \text { 或 }\infty, & \text { 若 }\left(v_{i}, v_{j}\right) \text { 或 }\left\langle v_{i}, v_{j}\right\rangle \text { 不是 } E(G) \text { 中的边 } \end{array}\right. A[i][j]={wij,0 或 ∞, 若 (vi,vj) 或 ⟨vi,vj⟩ 是 E(G) 中的边 若 (vi,vj) 或 ⟨vi,vj⟩ 不是 E(G) 中的边
2.图像示例
- 无向图和它的邻接矩阵可以表示为下图形式:
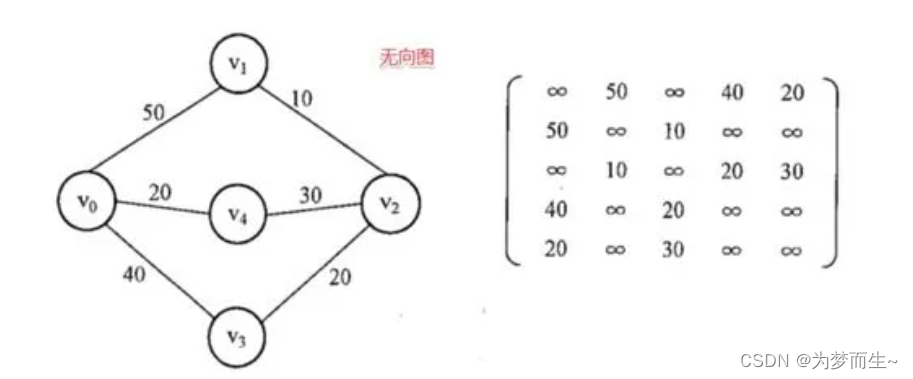
- 有向图和它的邻接矩阵可以表示为下图形式:
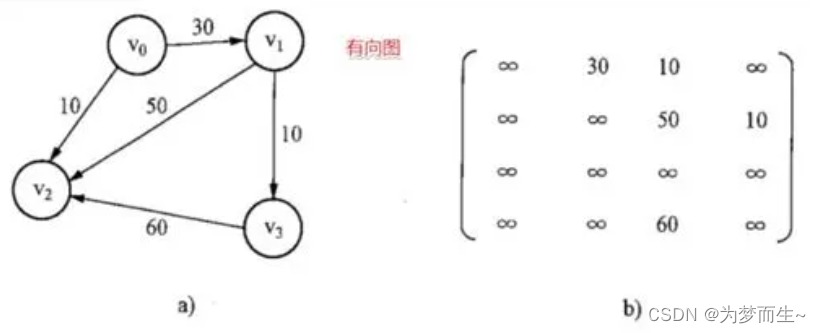
3. 代码实现
图的邻接矩阵代码实现:
#include<iostream>
#include<string>
#include<assert.h>
using namespace std;
#define MaxVertexNum 100 //顶点数目的最大值
#define INF 0xfffffff
//顶点的数据类型
typedef string VertexType;
//带权图中边上权值的数据类型
typedef int EdgeType;
//定义图的类型
typedef enum GraphType{
UDG, DG, UDN, DN
}GraphType;
//邻接矩阵数据结构定义
typedef struct{
VertexType Vex[MaxVertexNum]; //顶点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //边表
int vexnum, arcnum; //图的当前顶点数和弧数
GraphType type; //标记图的类型
}MGraph, *graph;
void graph_create(MGraph &g); //图的定义
int vertex_index(MGraph g, string v); //返回顶点v的坐标
void graph_add_vertex(MGraph &g, string v); //添加顶点
bool graph_has_vertex(MGraph &g, string v); //检查是否存在顶点v
void graph_add_edge(MGraph &g, string v1, string v2); //添加边
bool graph_has_edge(MGraph g, string v1, string v2); //检查是否存在v1->v2的边
void show_graph(MGraph g); //打印图
void graph_create(MGraph &g){
string str;
cout << "请输入要定义的图的类型:" << endl << "UDG(无向图) DG(有向图) UDN(无向网) DN(有向网)" << endl;
cin >> str;
//初始化邻接矩阵
for(int i = 0; i < g.vexnum; i++){
for(int j = 0; j < g.vexnum; j++){
if(i != j){
if(str == "UDN" || str == "DN")
g.Edge[i][j] = INF;
else g.Edge[i][j] = 0;
}
else g.Edge[i][j] = 0;
}
}
if(str == "UDG") g.type = UDG; //构建无向图
else if(str == "DG") g.type = DG; //构建有向图
else if(str == "UDN") g.type = UDN; //构建无向网
else if(str == "DN") g.type = DN; //构建有向网
}
void graph_add_vertex(MGraph &g, string v){
if(!graph_has_vertex(g, v)){
assert(g.vexnum <= MaxVertexNum);
g.Vex[g.vexnum++] = v;
}
}
bool graph_has_vertex(MGraph &g, string v){
for(int i = 0; i < g.vexnum; i++)
if(g.Vex[i] == v) return true;
return false;
}
void graph_add_edge(MGraph &g, string v1, string v2){
if(!graph_has_edge(g, v1, v2)){
int start = vertex_index(g, v1);
int end = vertex_index(g, v2);
if(g.type == UDG){
g.Edge[start][end] = 1;
g.Edge[end][start] = 1;
}else if(g.type == DG){
g.Edge[start][end] = 1;
}else if(g.type == UDN){
cout << "请输入边的权值:";
cin >> g.Edge[start][end];
g.Edge[end][start] = g.Edge[start][end];
}else if(g.type == DN){
cout << "请输入边的权值:";
cin >> g.Edge[start][end];
}
}
}
bool graph_has_edge(MGraph g, string v1, string v2){
int start = vertex_index(g, v1);
int end = vertex_index(g, v2);
assert(start != -1 && end != -1);
if(g.type == UDG || g.type == UDN){
//如果是无向图或无向网
if(g.Edge[start][end] != 0 && g.Edge[start][end] != INF) return true;
if(g.Edge[end][start] != 0 && g.Edge[end][start] != INF) return true;
}else if(g.type == DG || g.type == DN){
//如果是有向图或有向网
if(g.Edge[start][end] != 0 && g.Edge[start][end] != INF) return true;
}
return false;
}
int vertex_index(MGraph g, string v){
for(int i = 0; i < g.vexnum; i++){
if(g.Vex[i] == v) return i;
}
return -1;
}
void show_graph(MGraph g) {
cout << "图的邻接矩阵如下所示:" << endl;
for(int i = 0; i < g.vexnum; i++){
//cout << g.Vex[i] << " ";
for(int j = 0; j < g.vexnum; j++){
if(g.Edge[i][j] == INF)
cout << "∞" << " ";
else
cout << g.Edge[i][j] << " ";
}
cout << endl;
}
}
void test(MGraph &g){
int vexNum = 0, edgeNum = 0;
string str, str1, str2;
cout << "请输入图的顶点的数量:" << endl;
cin >> vexNum;
for(int i = 0; i < vexNum; i++){
cout << "输入顶点" << i+1 << "的信息:";
cin >> str;
graph_add_vertex(g, str);
}
cout << "请输入图的边的数量:" << endl;
cin >> edgeNum;
for(int i = 0; i < edgeNum; i++){
cout << "输入第" << i+1 << "条边的首尾顶点:";
cin >> str1 >> str2;
graph_add_edge(g, str1, str2);
}
}
int main(){
MGraph g;
graph_create(g);
test(g);
show_graph(g);
return 0;
}
当然,还可以根据需求,写一些个性化的函数来丰富图的功能。比如graph_destroy用来销毁图,graph_get_edge来获取边的权值,graph_edges_count计算与顶点v有关系的边的数量……
注意
- 在简单应用中,可直接用二维数组作为图的邻接矩阵(顶点信息等均可省略)。
- 当邻接矩阵的元素仅表示相应边是否存在时,EdgeType可采用值为0和1的枚举类型。
- 无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储。
- 邻接矩阵表示法的空间复杂度为 O ( n 2 ) \ O(n ^{2}) O(n2),其中n为图的顶点数 ∣ V ∣ \ |V| ∣V∣。
邻接矩阵的特点
- 无向图的邻接矩阵一定是一个对称矩阵(并且唯一)。因此,在实际存储邻接矩阵时只需存储上(或下)三角矩阵的元素。
- 对于无向图,邻接矩阵的第 i \ i i行(或第 i \ i i列)非零元素(或非 0 \ 0 0元素)的个数正好是顶点 i \ i i的度 T D ( v i ) \ TD(v _{i}) TD(vi)。
- 对于有向图,邻接矩阵的第 i \ i i行非零元素(或非 ∞ \ ∞ ∞元素)的个数正好是顶点 i \ i i的出度 O D ( v i ) \ OD(v _{i}) OD(vi);第 i \ i i列非零元素(或非 ∞ \ ∞ ∞元素)的个数正好是顶点i的入度 I D ( v i ) \ ID(v _{i}) ID(vi)。
- 用邻接矩阵存储图,很容易确定图中任意两个顶点之间是否有边相连。但是,要确定图中有多少条边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。
- 稠密图适合使用邻接矩阵的存储表示。
- 设图 G \ G G的邻接矩阵为 A \ A A, A n \ A ^{n} An的元素 A n [ i ] [ j ] \ A ^{n}[i][j] An[i][j]等于由顶点 i \ i i到顶点 j \ j j的长度为 n \ n n的路径的数目。该结论了解即可,证明方法请参考离散数学教材。
二、邻接表
1.概念
当一个图为稀疏图时,使用邻接矩阵法显然要浪费大量的存储空间,而图的邻接表法结合了顺序存储和链式存储方法,大大减少了这种不必要的浪费。
- 所谓邻接表,是指对图 G \ G G中的每个顶点 v \ v v建立一个单链表,第 i \ i i个单链表中的结点表示依附于顶点 v \ v v的边(对于有向图则是以顶点 v \ v v为尾的弧),这个单链表就称为顶点 v \ v v的边表(对于有向图则称为出边表)。
- 边表的头指针和顶点的数据信息采用顺序存储(称为顶点表),所以在邻接表中存在两种结点:顶点表结点和边表结点。
2.图像示例
-
顶点表结点的数据结构如下图所示:

-
边表结点的数据结构如下图所示:

顶点表结点由顶点域(data)和指向第一条邻接边的指针(firstarc)构成,边表结点(邻接表)由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc)构成。 -
无向图和它的邻接表可以表示为下图形式:
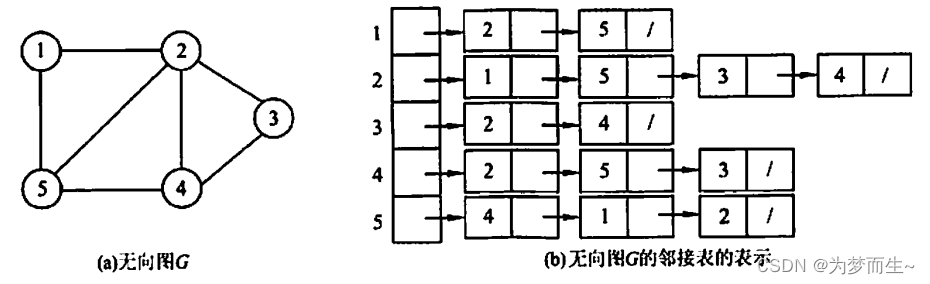
-
有向图和它的邻接表可以表示为下图形式:
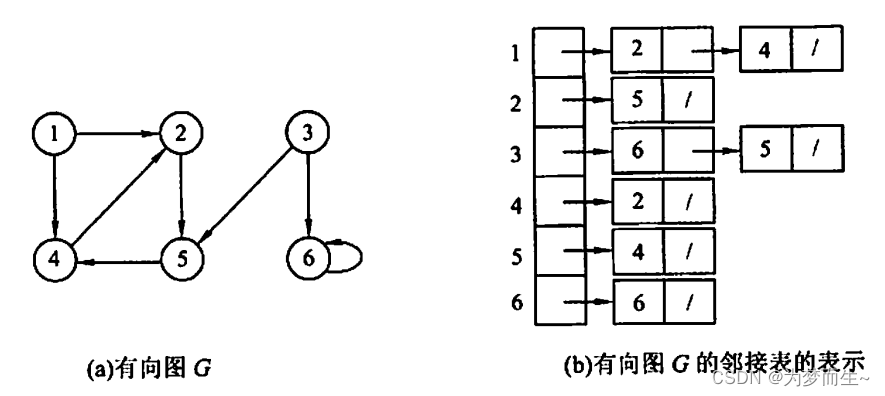
3.代码实现
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<string.h>
//#include<math.h>
#define string char*
#define VertexType string
#define MAXSIZE 100
#define REALLOCSIZE 50
#define INF 0xfffffff
//边表结点
typedef struct ArcNode{
int adjvex; //某条边指向的那个顶点的位置
ArcNode * next; //指向下一条弧的指针
weight w; //权值
}ArcNode;
//顶点表结点
typedef struct VNode{
VertexType data; //顶点信息
ArcNode * first; //指向第一条依附该顶点的弧的指针
}VNode;
typedef struct GraphRepr{
VNode * node; //邻接表
int vexnum, arcnum; //图的顶点数和弧数
}Graph, *graph;
graph graph_create(void) {
//初始化一个图的指针
graph g = (graph)malloc(sizeof(Graph));
if(g){
//初始化邻接表
g->node = (VNode*)malloc(MAXSIZE*sizeof(VNode));
if(!g->node) {
printf("error\n");
return NULL;
}
g->arcnum = g->vexnum = 0;
return g;
}
return NULL;
}
void graph_destroy(graph g) {
ArcNode *pre, *p; //定义临时指针
char * temp;
for(int i = 0; i < g->vexnum;i++){
pre = g->node[i].first; //指向边表
temp = g->node[i].data;
free(temp);
//等价于链表的销毁
if(pre != NULL) {
p = pre->next;
while(p != NULL) {
free(pre);
pre = p;
p = pre->next;
}
free(pre);
}
}
free(g);
return;
}
//判断字符串是否相等
bool is_equal(string s1, string s2){
//首先判断长度
int len_s1 = strlen(s1);
int len_s2 = strlen(s2);
if(len_s1 != len_s2) return false;
//长度相等后,判断每一个位置的字符
for(int i = 0; i < len_s1; i++)
if(s1[i] != s2[i]) return false;
return true;
}
void graph_add_vertex(graph g, string v) {
if(!graph_has_vertex(g, v)){
int vlen = strlen(v);
//判断是否超出邻接表的大小限制
if(g->vexnum+1 > MAXSIZE){
//重新申请一片空间
VNode * temp = (VNode*)malloc((g->vexnum+REALLOCSIZE)*sizeof(VNode));
//将原邻接表的信息复制到新的内存空间
for(int i = 0; i < g->vexnum; i++){
temp[i].data = g->node[i].data;
temp[i].first = g->node[i].first;
}
g->node = temp; //新的指针赋给邻接表
}
g->node[g->vexnum].data = (char*)malloc(sizeof(char)*vlen+1);
// printf("%p\t", strcpy(g->node[g->vexnum].data, v));
// printf("%p\t", g->node[g->vexnum].data);
// printf("%p\n", v);
// int i;
// for(i = 0; i < vlen; i++)
// g->node[g->vexnum].data[i] = v[i];
// v[i] = '\0';
g->node[g->vexnum].first = NULL; //初始化顶点的依附表结点为空
g->vexnum++;
}
return;
}
bool graph_has_vertex(graph g, string v) {
for(int i = 0; i < g->vexnum; i++)
if(is_equal(g->node[i].data, v)) //如果能够找到一个顶点的信息为v
return true;
return false;
}
size_t graph_vertices_count(graph g) {
return g->vexnum;
}
int get_index(graph g, string v){
for(int i = 0; i < g->vexnum; i++)
if(is_equal(g->node[i].data, v)) return i+1; //如果能找到这个结点,返回结点位置
return -1; //否则返回-1
}
void graph_add_edge(graph g, string v1, string v2, weight w){
//判断是否存在这两个顶点,如果不存在,添加这些顶点
if(!graph_has_vertex(g, v1)) graph_add_vertex(g, v1);
if(!graph_has_vertex(g, v2)) graph_add_vertex(g, v2);
int start = get_index(g, v1);
int end = get_index(g, v2);
//判断是否存在这条边
if(!graph_has_edge(g, v1, v2)){
//初始化一个边表结点
ArcNode * Next = (ArcNode*)malloc(sizeof(ArcNode));
Next->adjvex = end-1;
Next->next = NULL;
Next->w = w;
//如果start依附的边为空
if(g->node[start-1].first == NULL) g->node[start-1].first = Next;
else{
ArcNode * temp = g->node[start-1].first;//临时表结点
while(temp->next) temp = temp->next; //找到表结点中start-1这个结点的链表的最后一个顶点
temp->next = Next; //在该链表的尾部插入这个边表结点
}
g->arcnum++; //边的数量++
}
return;
}
bool graph_has_edge(graph g, string v1, string v2) {
int start = get_index(g, v1);
int end = get_index(g, v2);
//如果边表为空,则不存在边
if(g->node[start-1].first == NULL) return false;
ArcNode * temp = g->node[start-1].first; //临时表结点
while(temp) {
if(temp->adjvex == end-1) return true; //如果存在一条v1指向v2的边
temp = temp->next; //指针后移
}
return false;
}
weight graph_get_edge(graph g, string v1, string v2) {
double w;
//如果不存在这条边,返回0
if(!graph_has_edge(g, v1, v2)) return 0.0;
int start = get_index(g, v1);
int end = get_index(g, v2);
ArcNode * temp = g->node[start-1].first;
while(temp){
//找到v1指向v2的边,并返回weight
if(temp->adjvex == end-1) return temp->w;
temp = temp->next;
}
return 0.0;
}
void graph_show(graph g, FILE *output) {
//先打印每一个顶点信息
for(int i = 0; i < g->vexnum; i++){
fprintf(output, "%s\n", g->node[i].data);
// printf("%s\n", g->node[i].data);
}
//然后打印每一条边
for(int i = 0; i < g->vexnum; i++){
ArcNode * Next = g->node[i].first;
while (Next) {
fprintf(output, "%s %s %10.2lf\n", g->node[i].data, g->node[Next->adjvex].data, Next->w);
// printf("%s %s %10.2lf\n", g->node[i].data, g->node[Next->adjvex].data, Next->w);
Next = Next->next;
}
}
return;
}
邻接表的特点
- 若 G \ G G为无向图,则所需的存储空间为 O ( ∣ V ∣ + 2 ∣ E ∣ ) \ O(|V|+ 2|E|) O(∣V∣+2∣E∣);若 G \ G G为有向图,则所需的存储空间为 O ( ∣ V ∣ + ∣ E ∣ ) \ O(|V|+ |E|) O(∣V∣+∣E∣)。前者的倍数 2 \ 2 2是由于无向图中,每条边在邻接表中出现了两次。
- 对于稀疏图,采用邻接表表示将极大地节省存储空间。
- 在邻接表中,给定一顶点,能很容易地找出它的所有邻边,因为只需要读取它的邻接表。在邻接矩阵中,相同的操作则需要扫描一行,花费的时间为 O ( n ) \ O(n) O(n)。
- 但是,若要确定给定的两个顶点间是否存在边,则在邻接矩阵中可以立刻查到,而在邻接表中则需要在相应结点对应的边表中查找另一结点,效率较低。
- 在有向图的邻接表表示中,求一个给定顶点的出度只需计算其邻接表中的结点个数;但求其顶点的入度则需要遍历全部的邻接表。因此,也有人采用逆邻接表的存储方式来加速求解给定顶点的入度。当然,这实际上与邻接表存储方式是类似的。
- 图的邻接表表示并不唯一,因为在每个顶点对应的单链表中,各边结点的链接次序可以是任意的,它取决于建立邻接表的算法及边的输入次序。