前几期的推送已经讲解了网络计划的基本知识、数学模型和相关算法，相信大家对网络计划已经有了充分的了解，这期小编将带大家一起来读一篇基于关键路径的置换流水车间调度问题的文章。

1.文章信息

题目：An efficient critical path based method for permutation flow shop scheduling problem

作者：Yang Li，Xinyu Li，Liang Gao，Ling Fu，Cuiyu Wang

来源：Journal of Manufacturing Systems

出版信息：Volume 63，April 2022，Pages 344-353

网址：Redirectinghttps://doi.org/10.1016/j.jmsy.2022.04.005Redirecting

2.文章导读

置换流水车间调度问题（The permutation flow shop scheduling problem，PFSP）广泛存在于汽车、船舶、装备制造、电子信息产品等制造企业中，是对经典的流水车间调度问题进行简化后得到的一类子问题。PFSP是一个著名的NP难题，随着作业和机器数量的增加，问题的解空间和求解难度都会迅速增加，要在短时间内得到满意的解决方案非常困难。PFSP问题最初的研究集中在数学规划方法上，如整数规划、分支定界等。随着问题规模的增大，数学规划方法的计算效率逐渐降低，在可接受的代价下得到组合优化问题可行解的启发式方法成为后续研究的主流。如今，随着人工智能技术的兴起和计算机技术的发展，智能优化方法逐渐发展起来，如禁忌搜索（Tabu Search，TS）、模拟退火（Simulated Annealing，SA）、遗传算法（Genetic Algorithm，GA）、人工蜂群算法（Ant colony optimization，ACO）等，极大地推动了PFSP的研究，多种元启发式方法组合使用的混合算法也成为研究的热点。然而，对于大规模PFSP（工件数≥100），这些元启发式算法的求解速度依旧不适用于实际生产，且从计算精度的角度来看，元启发式算法的结果具有随机性，难以用于指导实际生产。因此，必须找到新的方法来加快算法的计算速度，同时保证解的质量。

3.摘要

置换流水车间调度问题是大规模定制生产中最重要、最典型的调度类型之一，也是一个著名的NP难题。然而，已有的算法大多缺乏理论指导，难以达到较好的精度和效率。针对这一问题，本文提出了一种基于关键路径的快速搜索方法，并给出了PFSP的三个定理及证明。首先，根据PFSP的特点，定义了关键路径和关键点的概念，并在此基础上，提出了一种新的求解PFSP的邻域搜索方法。在每次邻域搜索中，只需要计算加工序列中的第一个和最后一个工件以及关键路径上每台机器的第一个工件的相邻工件，无论问题规模有多大，该方法最多只需搜索（2m+2）次就能找到最优邻域解（m为机器数）。最后，将新的邻域搜索方法与改进的模拟退火算法相结合求解PFSP。为了验证所提算法的性能，本文在TA测试平台上与现有算法进行了对比实验，实验结果表明，本文提出的方法取得了明显的改进，在相同的算法框架下，该方法可以减少平均35.2%的计算时间。

4.主要内容

PFSP研究的是n个工件在m台机器上的流水加工过程，所有工件以相同的顺序在每一台机器上加工完成（加工顺序相同但每个加工步骤的工艺可能不同），同时要求每个工件在每台机器上只加工一次，每台机器每次最多只能加工一个工件，各工件在各机器上所需的加工时间已知，目标是找到使完成时间最小化的作业顺序。PFSP的解由n个作业的排列表示，即σ={σ1，σ2，…，σn}，Cσj,m表示工件σj在机器m上的完成时间，tij表示工件i在机器j上的加工时间，完成时间计算如下：

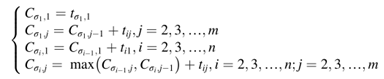
 从公式可以看出，每个完工时间的计算都有一定的复杂度，随着作业数量的增加，求解时间将呈指数增长。因此，对于大型车间来说，如何缩短完工时间的计算时间是必须思考的问题。JSP（单车间调度问题）中经常使用关键路径来加快搜索过程，它被定义为从第一个作业的第一步到最后一个作业的最后一步的最长路径，关键路径有一个重要的性质，即交换非关键路径的过程不影响最终的完工时间。以该定义为标准，关键路径仍然可以在PFSP中找到，如图1所示的例子中，20个工件在5个机器上流水加工，关键路径可由红色箭头表示，且对PFSP来说，由于在不同的机器上加工工艺的顺序均相同，因此所有的工件都在关键路径上。

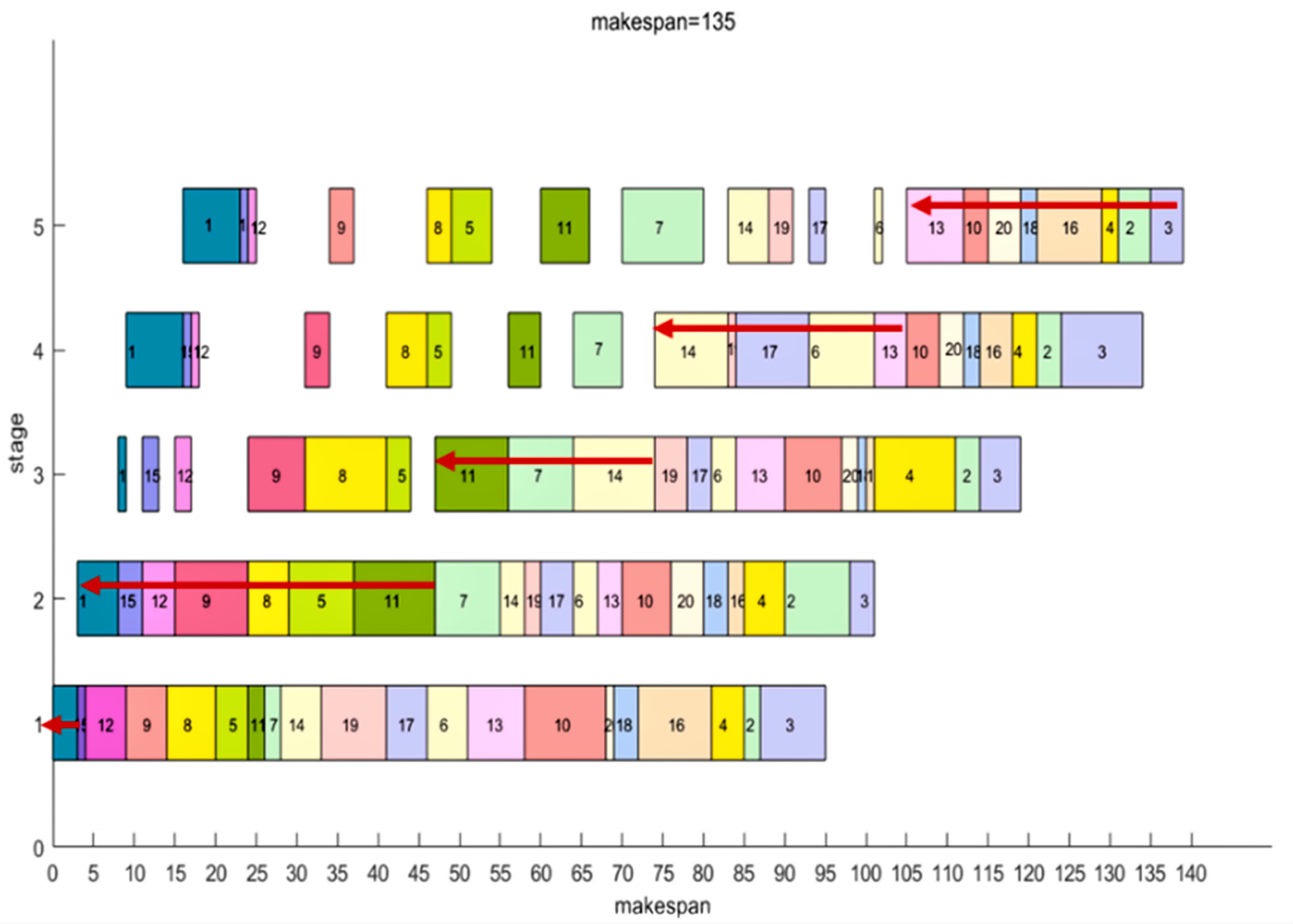
 图1 PFSP的关键路径

本文通过邻域搜索来获得最优解，并将有效的邻域搜索定义如下：相邻工件的加工顺序依次交换，如果解的质量变好，则保留当前的加工顺序并继续交换；否则，交换作业顺序，直到解决方案的质量无法提高为止，此时，可以获得局部最优解。

为了提高搜索速度、节约搜索时间，本文还定义了关键块和关键点的概念，结合上述20个工件在5个机器上流水加工的例子进行讲解。图2是PFSP的甘特图，对于图中工件8和5的交换，求解交换后的最大完工时间需要重新计算，这会花费很长时间。而甘特图表明，交换相邻的8和5工件后，整体结构变化并不大，因此整个调度结果的变化可以用红色区域来表示，本文将这里的红色区域定义为关键块。

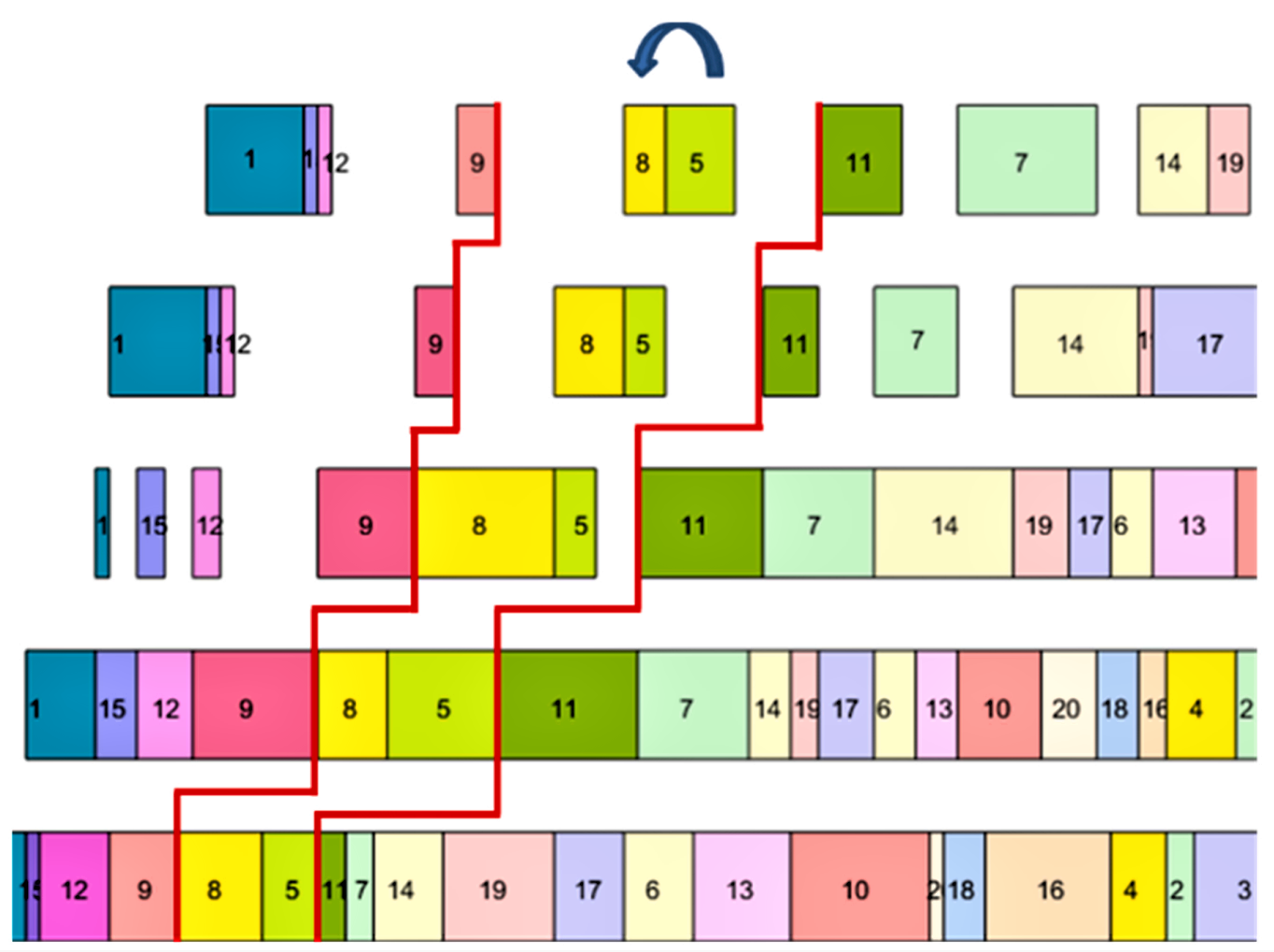
 图2 PFSP的关键块

另外，将图1的关键路径与图2所示的关键块结合起来，关键点被定义为关键路径和关键块的交点（如图中蓝色圈起来的部分为关键点）。通过研究和数学证明，本文给出了关键点的三个性质：

定理1.如果交换相邻作业后关键点的开始时间增加，解的质量一定不会变好；而如果关键点的开始时间减少，则解的质量一定不会变差。

定理2.在关键路径上，如果同一台机器上有4个或更多的工序相邻，当任意两个非外部工序对应的工件交换时，总加工时间不会缩短。

推论3.该邻域只需要计算加工序列中的第一个和最后一个工件，以及关键路径上每台机器的第一个工件的相邻工件。

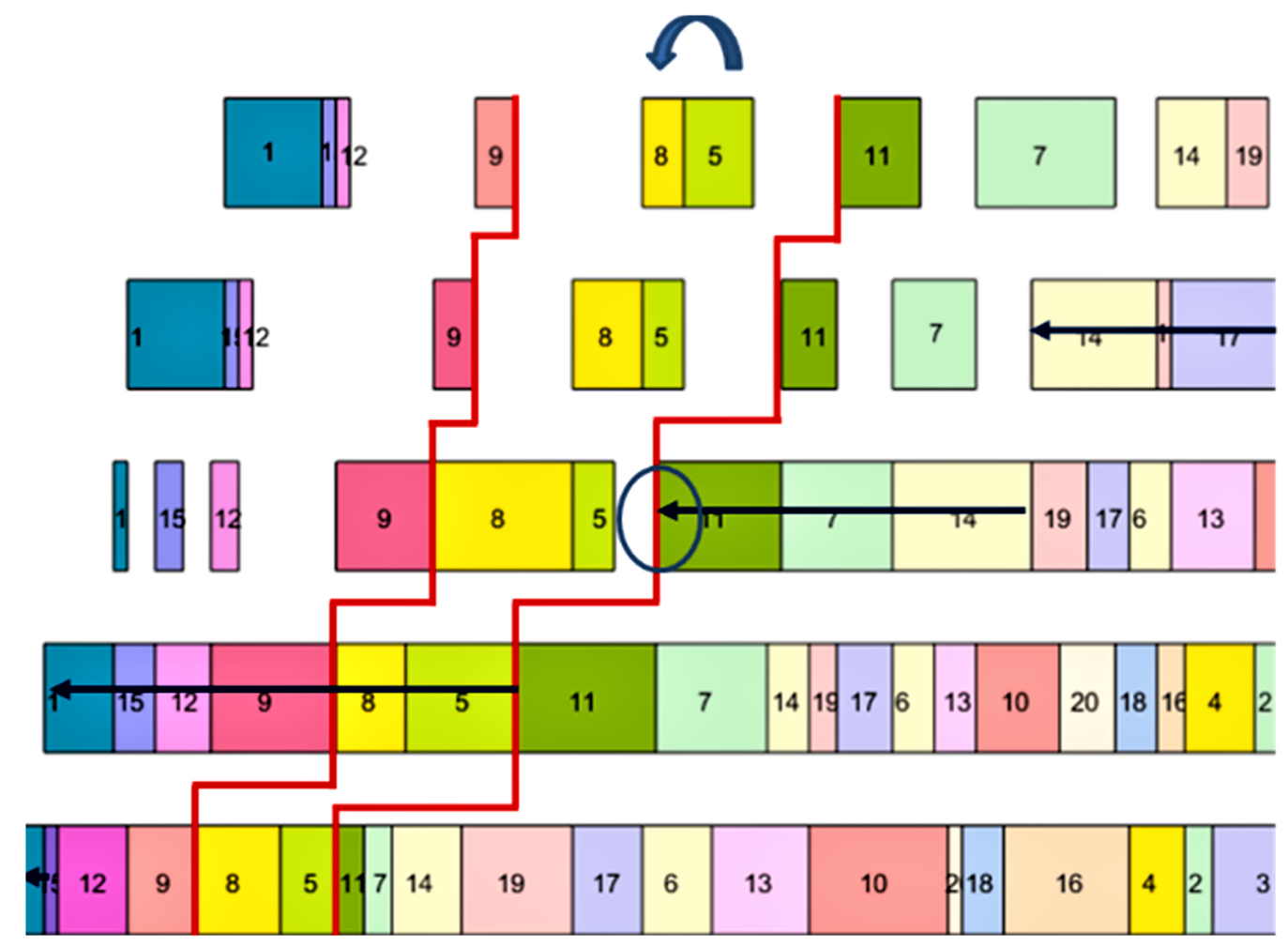
 图3 PFSP的关键点

结合甘特图和定理1、定理2与推论3，在每次邻域搜索中，只需要计算加工序列中的第一个和最后一个工件以及关键路径上每台机器的第一个工件的相邻工件，无论问题规模有多大，该方法最多只需搜索（2m+2）次就能找到最优邻域解（m为机器数）。例如，在图4中，当前邻域只需要搜索作业1和15、5和11、11和7、7和14、6和13、2和3，然后利用定理1对这6组工件进行简化计算后，便可得到局部最优解，从而加快了邻域搜索的速度。

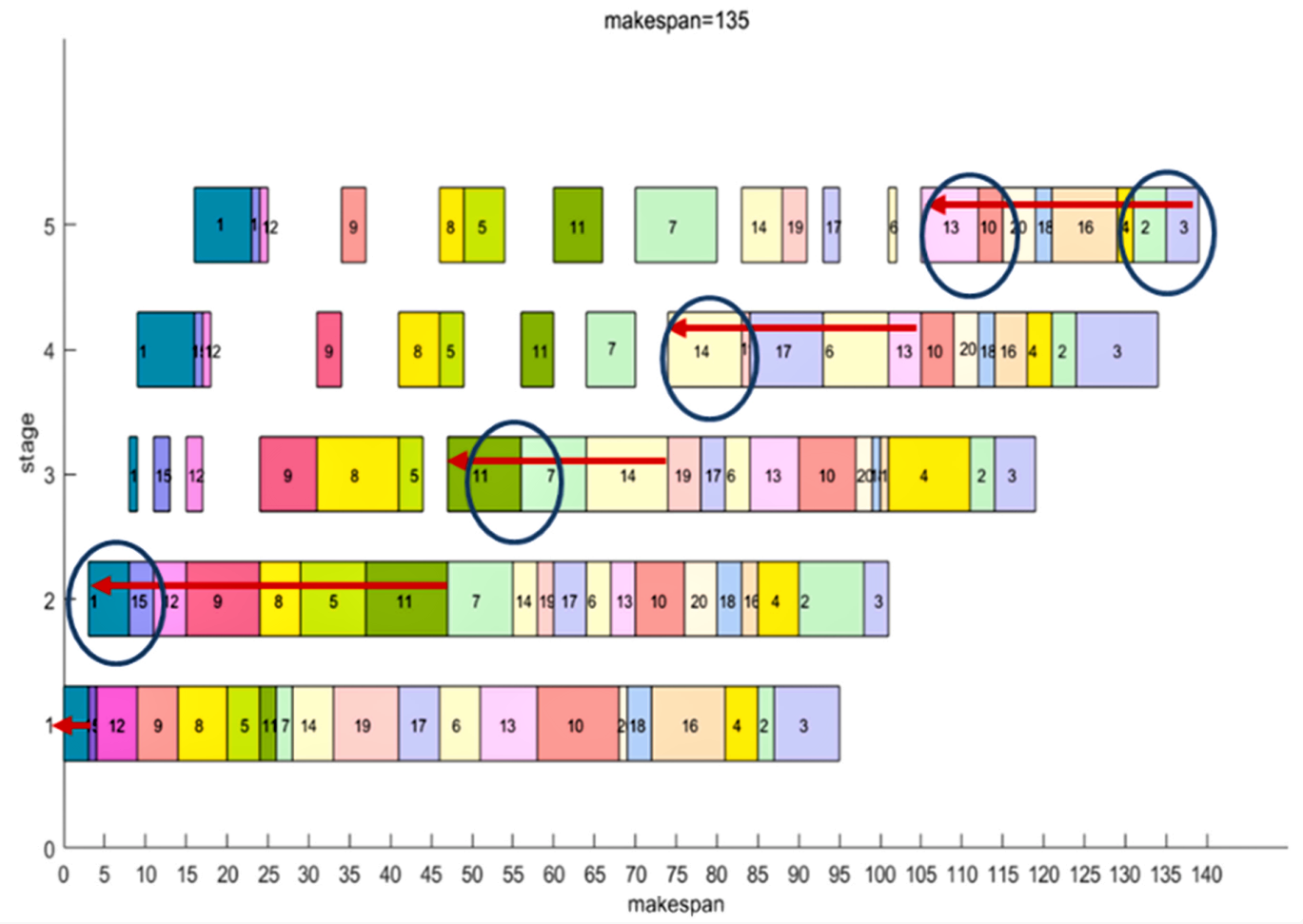
 图4 PFSP邻域搜索方法

综合上述的关键块、关键点及三条定理，本文给出了邻域搜索的总体框架，如图5所示。第一步：输入初始加工顺序，求解关键路径。第二步：如果遍历了所有作业，则输出局部最优解；否则，继续执行步骤三。第三步：交换下一个相邻作业（需要交换的作业由推论3计算），通过关键点的移动快速判断解的质量变化，如果解的质量变好，则更新序列和关键路径；否则，保持序列和关键路径不变，返回步骤二。

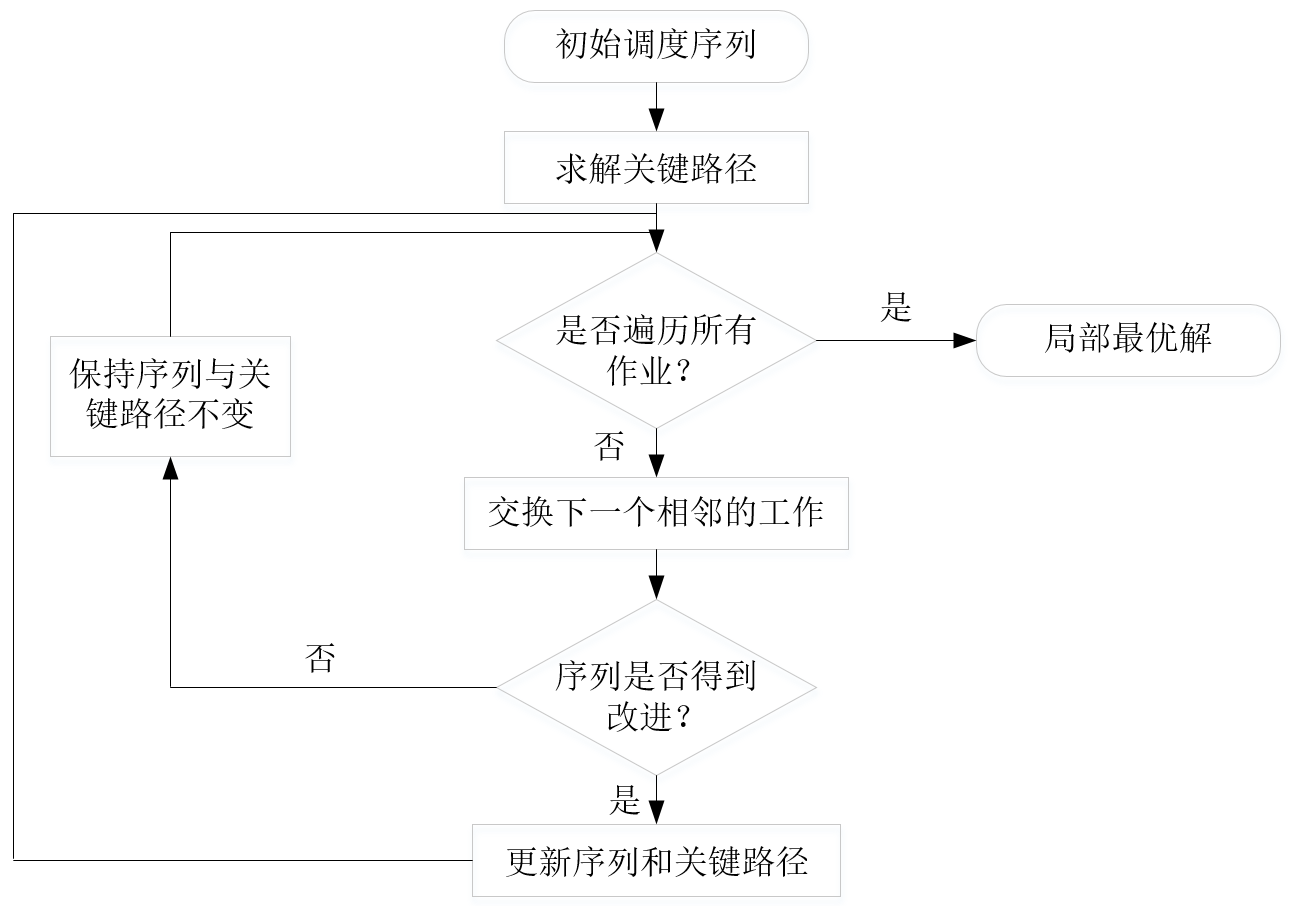
 图5 PFSP的邻域搜索框架

由于PFSP的邻域搜索方法在实际应用中需要与元启发式算法相结合，故本文选择并改进了1983年Kirkpatrick等人提出的基于Metropolis准则的SA算法，得到了基于邻域搜索的改进SA算法“NS-SA”。改进后的“NS-SA”算法的具体计算框架如图6所示。

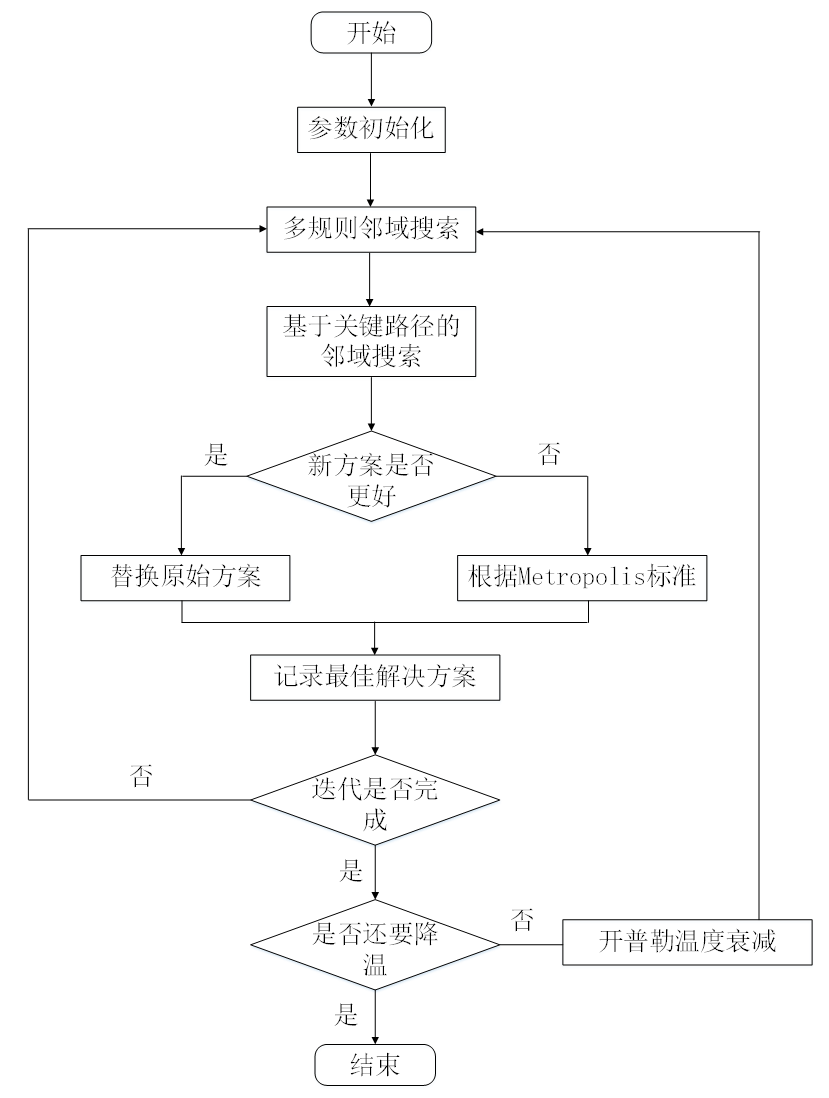
 图6 NS-SA算法框架

根据“NS-SA”算法的框架，该算法引入了基于关键路径的邻域搜索，可以在更短的时间内搜索到更多的解空间，且每次温度搜索都能保证一定的局部最优解，增强了元启发式算法的稳定性。此外，与SA算法相比，该算法的改进主要集中在以下三个方面：

（1）参数初始设置

本文采用自然数编码方式，即n个作业被连续编号为1-n，初始解由NEH算法生成。由于初始温度将影响接受劣质解的概率，因此为保证初始概率的准确性，本文采用的初始温度计算公式为T0=(- Δmax)/P0，其中P0是初始接受概率，|Δmax|表示一组随机解之间的最大适应性差异。

（2）更新新解方式

本文采用基于概率选择的多规则邻域搜索操作来协作更新新解，采用的邻域搜索操作包括三种：

①二进制交换：随机选择序列中的两个点，并颠倒它们之间所有作业的顺序；

②三点兑换：随机选择序列中的三个点，并交换它们之间的两个位置；

③两点兑换：随机选择序列中的两个点，并交换这两个点的工作。

本文在同一温度下，对初始序列进行三次独立的搜索，然后选取最优值作为提出的“NS-SA”算法的初始解。

（3）温度衰减函数

本文用开普勒型衰变函数代替了原来的指数函数，开普勒型衰减函数递减曲线公式如下：

 K和k分别表示迭代次数和总冷却时间，当温度衰减到终止温度时算法程序结束。

5.结论

PFSP作为一个经典的NP难题，随着作业和机器数量的增加，问题的解空间和求解难度都会迅速增加。本文针对这一问题，定义了PFSP的关键路径与关键点，并在此基础上提出了一种基于关键路径的快速搜索方法。在每次邻域搜索中，只需要计算加工序列中的第一个和最后一个工件以及关键路径上每台机器的第一个工件。无论问题规模有多大，该方法最多只需搜索（2m+2）次就能找到最优邻域解（m为机器数）。最后，将新的邻域搜索方法与改进的模拟退火算法相结合求解PFSP。

为了验证所提算法的性能，本文在TA测试平台上进行实验。根据在测试平台上的测试结果，“NS-SA”算法得到了38个最优解，其中22个达到了已知的上界。特别是在TA116测试平台中，本文得到的结果超过了网站上公布的当前最优解，这证明本文提出的方法对求解PFSP是有效可靠的，可以大大提高解的质量。另外，本文比较了邻域搜索过程和整个算法所花费的时间，根据测试结果，本文提出的改进算法的计算速度平均提高了35.2%，整体计算时间显著减少。最后，为了验证算法的鲁棒性，本文选取TA61-TA65作为算例，每种情况下测试10次，平均标准差仅为2.4437，证明了算法的鲁棒性。

6.贡献

1、本文根据PFSP的特点，定义了关键路径、关键块和关键点的概念，将车间调度问题中关键路径的概念引入到PFSP问题，并通过研究和数学证明，给出了PFSP的三个定理及相关证明。

2、本文分析了PFSP的本质，并结合PFSP的三个定理提出了一种基于关键路径的PFSP邻域搜索方法。在每次邻域搜索中，无论问题的规模有多大，该方法最多只需搜索（2 m+2）次就能找到最优邻域解（m为机器数），大大减少了计算量，提高了搜索精度。

3、文章将新的邻域搜索方法与改进的模拟退火算法相结合，得到了基于邻域搜索的改进SA算法“NS-SA”，改进的SA算法可以在更短的时间内搜索到更多的解空间，增强了元启发式算法的稳定性。

4、本文提出的邻域搜索方法还可以与其他元启发式算法相结合，也可以推广到PFSP的变体，具有广泛的应用空间。

7.展望

本文提出了一种基于关键路径的PFSP的邻域搜索方法，通过对PFSP本质的研究找到了相应的规律定理并将其应用于算法求解中，大大减少了算法的计算量，提高了算法的搜索精度。本文虽然取得了较好的效果，但仍存在一定的局限性：首先，本文提出的算法应用范围有限，仅适用于置换流水车间调度问题及其变体，无法进行大规模推广。其次，本文提出的算法中，更新新解的邻域搜索方法只适用于相邻工件的互换操作，无法解决插入操作，因此在某些特定的应用场景下，该算法可能无法完全满足需求。

因此，在今后的工作中，可以结合不同的调度问题进一步分析其数学模型，寻找更适合的邻域搜索方法应用于算法求解。另外还可以考虑在调度过程中新增任务的动态事件对调度方案的影响，进一步改进邻域搜索方法，为车间调度问题的解决提供帮助。

作者 | 隋朝阳 王一静

责编 | 陈梦   

审核 | 徐小峰

YUNCHOUSHUO· 

· 知乎｜运筹说 ·

· 简书｜运筹说 ·

·哔哩哔哩 | 运筹说 ·