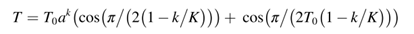假设神经网络同列数字之间有一种排斥力,且这种排斥力也与距离的平方成反比。设0是环境,1是粒子,则两个1之间的排斥力就是距离平方的倒数。
考虑任意遥远的两个粒子之间都有排斥力,可以得到同列排斥力的计算方法为

如计算"01001111111"的排斥力
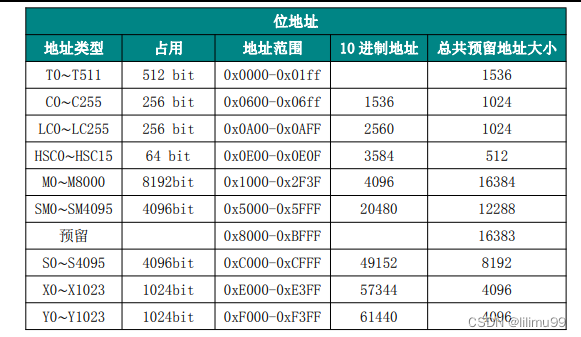
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
将力F具体展开

如计算第一项r14=3,F14=0.111

其余各项为
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 0 | |||||||||||||||||||
| 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0.111 | 0.063 | 0.04 | 0.028 | 0.02 | 0.016 | 0.012 | |||||
| 2 | |||||||||||||||||||
| 3 | |||||||||||||||||||
| 4 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 0.25 | 0.111 | 0.063 | 0.04 | 0.028 | |||||||
| 5 | 1 | 2 | 3 | 4 | 5 | 1 | 0.25 | 0.111 | 0.063 | 0.04 | |||||||||
| 6 | 1 | 2 | 3 | 4 | 1 | 0.25 | 0.111 | 0.063 | |||||||||||
| 7 | 1 | 2 | 3 | 1 | 0.25 | 0.111 | |||||||||||||
| 8 | 1 | 2 | 1 | 0.25 | |||||||||||||||
| 9 | 1 | 1 | |||||||||||||||||
| 10 |
将所有项相加F01001111111=8.2795.左右相同。
( A, B )---1*30*2---( 1, 0 )( 0, 1 )
用这种方法计算同列有3个0和8个1的其他各项得到
| 迭代次数 | 排斥力 | ||
| "00011111111" | 3+f1 | 20470.21 | 9.50152 |
| "01001111111" | 3+f2 | 21099.48 | 8.27949 |
| "00101111111" | 3+f3 | 21759.81 | 8.51714 |
| "01100111111" | 3+f4 | 21810.68 | 7.95441 |
| "01110011111" | 3+f5 | 22313.81 | 7.82899 |
| "01010111111" | 3+f6 | 22402.91 | 7.43879 |
| "01111001111" | 3+f7 | 22920.43 | 7.79426 |
| "00110111111" | 3+f8 | 22920.3 | 8.28755 |
| "01101011111" | 3+f9 | 23066.35 | 7.16969 |
| "00111011111" | 3+f10 | 23183.93 | 8.20422 |
| "01110101111" | 3+f11 | 23570.92 | 7.07899 |
| "01011011111" | 3+f12 | 23729.11 | 7.26518 |
| "01011101111" | 3+f13 | 24086.94 | 7.21656 |
| "01101101111" | 3+f14 | 24342.91 | 7.0308 |
| "01110111011" | 3+f15 | 24833.37 | 7.01691 |
将迭代次数画成图
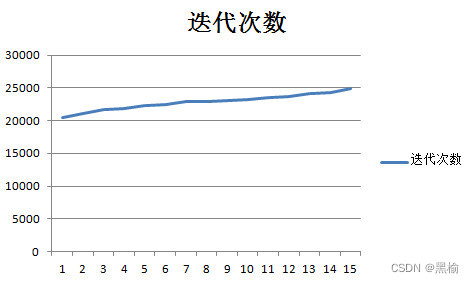
比较排斥力
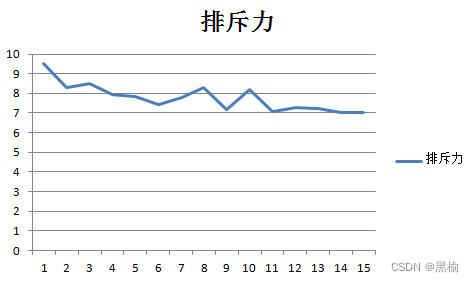
排斥力与迭代次数成反比,将这一列数据想象成一条纸带,纸带上镶嵌有粒子,粒子之间的排斥力越大,纸带越不稳定,所以迭代次数描述的是这个系统的稳定性。