本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
There are n piles of stones arranged in a row. The ith pile has stones[i] stones.
A move consists of merging exactly k consecutive piles into one pile, and the cost of this move is equal to the total number of stones in these k piles.
Return the minimum cost to merge all piles of stones into one pile. If it is impossible, return -1.
Example 1:
Input: stones = [3,2,4,1], k = 2
Output: 20
Explanation: We start with [3, 2, 4, 1].
We merge [3, 2] for a cost of 5, and we are left with [5, 4, 1].
We merge [4, 1] for a cost of 5, and we are left with [5, 5].
We merge [5, 5] for a cost of 10, and we are left with [10].
The total cost was 20, and this is the minimum possible.
Example 2:
Input: stones = [3,2,4,1], k = 3
Output: -1
Explanation: After any merge operation, there are 2 piles left, and we can't merge anymore. So the task is impossible.
Example 3:
Input: stones = [3,5,1,2,6], k = 3
Output: 25
Explanation: We start with [3, 5, 1, 2, 6].
We merge [5, 1, 2] for a cost of 8, and we are left with [3, 8, 6].
We merge [3, 8, 6] for a cost of 17, and we are left with [17].
The total cost was 25, and this is the minimum possible.
Constraints:
n == stones.length1 <= n <= 301 <= stones[i] <= 1002 <= k <= 30
题意:有 N 堆石头排成一排,第 i 堆中有 stones[i] 块石头。每次移动(move)需要将连续的 K 堆石头合并为一堆,而这个移动的成本为这 K 堆石头的总数。找出把所有石头合并成一堆的最低成本。如果不可能,返回 -1 。
相似题目(区间 DP)
- 猜数字大小 II
- 最长回文子序列
- 多边形三角剖分的最低得分
- 让字符串成为回文串的最少插入次数
- 切棍子的最小成本
解法1 记忆化搜索
不可能合并为一堆的情况是最简单的。从 n n n 堆变成 1 1 1 堆,需要减少 n − 1 n - 1 n−1 堆,每次合并会减少 k − 1 k - 1 k−1 堆,所以 n − 1 n - 1 n−1 必须是 k − 1 k - 1 k−1 的倍数。
再通过一个例子思考能合并的情况,比如一开始有
7
7
7 堆石头,
k
=
3
k = 3
k=3 。最后一步会发生什么?很简单,由
3
3
3 堆合并为
1
1
1 堆。注意:合并石头不会改变石头的总数,所以合并这
3
3
3 堆石头的成本等于
3
3
3 堆石头的总数、也等于原来的
7
7
7 堆石头的总数(后面会用到这个结论)。
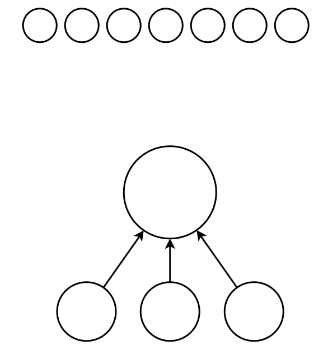
继续思考:这
3
3
3 堆中的第一堆是怎么合并的?有以下几种情况:
- 就是 s t o n e s [ 0 ] stones[0] stones[0] ,无需合并
- 由 s t o n e s [ 0 : 2 ] stones[0:2] stones[0:2] 进行 1 1 1 次合并得到
- 由 s t o n e s [ 0 : 4 ] stones[0:4] stones[0:4] 通过 2 2 2 次合并得到。具体这两次是怎么合并的,还需要继续计算。
- ……

而对于右边剩余的石头堆,需要计算的问题是:把这些石头堆合并为 2 2 2 堆的最低成本。
到这里了,应该能从中总结出一个和原问题相似的子问题了。找到了原问题和子问题的关系,就能通过递归(记忆化搜索)的方式解决。显然,问题是「求出把 s t o n e s [ i : j ] stones[i:j] stones[i:j] 合并为 p p p 堆的最低成本」,定义 d f s ( i , j , p ) dfs(i,j,p) dfs(i,j,p) 表示这个问题的解。
于是对
7
7
7 堆石头有
d
f
s
(
0
,
6
,
1
)
dfs(0, 6, 1)
dfs(0,6,1) ,它等于
d
f
s
(
0
,
6
,
3
)
+
∑
i
=
0
6
s
t
o
n
e
s
[
i
]
dfs(0, 6, 3) +\displaystyle \sum^6_{i=0} stones[i]
dfs(0,6,3)+i=0∑6stones[i] ,而
d
f
s
(
0
,
6
,
3
)
dfs(0, 6, 3)
dfs(0,6,3) 又等于下面几种情况的最小值:
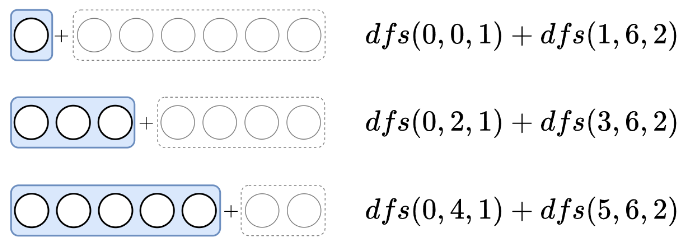
总结如下:
d
f
s
(
i
,
j
,
1
)
=
d
f
s
(
i
,
j
,
k
)
+
∑
q
=
i
j
子数组和可以用前缀和优化
d
f
s
(
i
,
j
,
p
)
=
min
m
=
i
+
(
k
−
1
)
x
{
d
f
s
(
i
,
m
,
1
)
+
d
f
s
(
m
+
1
,
j
,
p
−
1
)
}
p
≥
2
\begin{matrix} dfs(i, j, 1) = dfs(i, j, k) + \sum^j_{q=i} \quad 子数组和可以用前缀和优化 \\ dfs(i, j, p) = \min_{m=i+(k-1)x} \bigg\{ dfs(i, m, 1) + dfs(m + 1, j, p -1) \bigg\} \quad p \ge 2\end{matrix}
dfs(i,j,1)=dfs(i,j,k)+∑q=ij子数组和可以用前缀和优化dfs(i,j,p)=minm=i+(k−1)x{dfs(i,m,1)+dfs(m+1,j,p−1)}p≥2
- 递归边界: d f s ( i , i , 1 ) = 0 dfs(i, i,1) =0 dfs(i,i,1)=0 ,只有一堆石头,不用合并,代价为 0 0 0
- 递归入口: d f s ( 0 , n − 1 , 1 ) dfs(0, n-1,1) dfs(0,n−1,1) 把所有石头堆合并为一堆的最小代价
代码实现时,由于整个递归中有大量重复递归调用(递归入参相同),且递归函数没有副作用(同样的入参无论计算多少次,算出来的结果都是一样的),因此可用记忆化搜索来优化:
- 如果一个状态(递归入参)是第一次遇到,那么可以在返回前,把状态及其结果记到一个 d p dp dp 数组(或哈希表)中。
- 如果一个状态不是第一次遇到,那么直接返回 d p dp dp 中保存的结果。
问:为什么只考虑分出 1 1 1 堆和 p − 1 p-1 p−1 堆,而不考虑分出 x x x 堆和 p − x p-x p−x 堆?
答:无需计算,因为 p − 1 p-1 p−1 堆继续递归又可以分出 1 1 1 堆和 p − 2 p-2 p−2 堆,和之前分出的 1 1 1 堆组合,就已经能表达出「分出 2 2 2 堆和 p − 2 p−2 p−2 堆」的情况了。其他同理。所以只需要考虑分出 1 1 1 堆和 p − 1 p-1 p−1 堆。
class Solution {
public:
int mergeStones(vector<int> &stones, int k) {
int n = stones.size();
if ((n - 1) % (k - 1) != 0) return -1; // 不能合并为一堆
int sum[n + 1]; memset(sum, 0, sizeof(sum));
for (int i = 0; i < n; ++i) sum[i + 1] = sum[i] + stones[i];
int dp[n][n][k + 1]; memset(dp, -1, sizeof(dp)); // -1表示没计算过
// dp[i][j][p]: 把stones[i:j]合并为p堆的最低成本
function<int(int, int, int)> dfs = [&](int i, int j, int p) -> int {
int &ans = dp[i][j][p];
if (ans != -1) return ans;
if (p == 1) { // 将stones[i:j]中的k堆石头合并为1堆,成本为这K堆石头数的和
return ans = i == j ? 0 : dfs(i, j, k) + sum[j + 1] - sum[i]; // 当然,先要将stones[i:j]的石头合并为k堆
}
ans = INT_MAX;
for (int m = i; m < j; m += (k - 1)) // [m,m+k)
ans = min(ans, dfs(i, m, 1) + dfs(m + 1, j, p - 1));
return ans;
};
return dfs(0, n - 1, 1);
}
};
复杂度分析:
- 时间复杂度: O ( n 3 ) O(n^3) O(n3) ,其中 n n n 为 s t o n e s stones stones 的长度。这里状态个数为 n 2 k n^2k n2k 个,单个状态的计算时间为 O ( n k ) O(\dfrac{n}{k}) O(kn) ,因此时间复杂度为 O ( n 3 ) O(n^3) O(n3)
- 空间复杂度: O ( n 2 k ) O(n^2k) O(n2k) 。
下面进行优化:把
d
f
s
(
i
,
j
,
1
)
dfs(i, j,1)
dfs(i,j,1) 改写成下面的式子,
p
p
p 就取不到
k
k
k 了,即
1
≤
p
<
k
1\le p < k
1≤p<k :
d
f
s
(
i
,
j
,
1
)
=
min
m
=
i
+
(
k
−
1
)
x
)
{
d
f
s
(
i
,
m
,
1
)
+
d
f
s
(
m
+
1
,
j
,
k
−
1
)
}
+
∑
q
=
i
j
s
t
o
n
e
s
[
q
]
dfs(i,j,1) = \min_{m=i+(k-1)x)} \bigg \{dfs(i, m, 1) + dfs(m + 1, j, k - 1) \bigg\} + \sum^j_{q=i} stones[q]
dfs(i,j,1)=m=i+(k−1)x)min{dfs(i,m,1)+dfs(m+1,j,k−1)}+q=i∑jstones[q]
由于枚举 m m m 时,保证 m − i m - i m−i 是 k − 1 k - 1 k−1 的倍数:
- 所以对于 d f s ( i , j , 1 ) dfs(i, j, 1) dfs(i,j,1) 来说, j − i j - i j−i 必然是 k − 1 k - 1 k−1 的倍数。
- 而对于 d f s ( i , j , p ) ( p ≥ 2 ) dfs(i, j, p)\ (p\ge 2) dfs(i,j,p) (p≥2) 来说, j − k j - k j−k 必然不是 k − 1 k - 1 k−1 的倍数(否则可以合并成一堆)。
- 所以通过判断 j − i j - i j−i 是否为 k − 1 k - 1 k−1 的倍数,就能知道 p = 1 p = 1 p=1 还是 p ≥ 2 p \ge 2 p≥2 。所以第三个参数 p p p 其实是多余的。
化简后,
d
f
s
(
i
,
j
)
dfs(i,j)
dfs(i,j) 表示把从
i
i
i 到
j
j
j 的石头堆合并到小于
k
k
k 堆的最小代价:
d
f
s
(
i
,
j
)
=
{
min
m
=
i
+
(
k
−
1
)
x
)
{
d
f
s
(
i
,
m
)
+
d
f
s
(
m
+
1
,
j
)
}
+
∑
q
=
i
j
s
t
o
n
e
s
[
q
]
(
j
−
i
)
m
o
d
(
k
−
1
)
=
0
min
m
=
i
+
(
k
−
1
)
x
)
{
d
f
s
(
i
,
m
)
+
d
f
s
(
m
+
1
,
j
)
}
(
j
−
i
)
m
o
d
(
k
−
1
)
≠
0
dfs(i,j)= \begin{cases} \min_{m=i+(k-1)x)} \bigg \{dfs(i, m) + dfs(m + 1, j) \bigg\} + \sum^j_{q=i} stones[q] \quad& (j-i)\bmod (k-1)=0\\ \min_{m=i+(k-1)x)} \bigg \{dfs(i, m) + dfs(m + 1, j) \bigg\} \quad& (j-i)\bmod (k-1)\ne 0 \end{cases}
dfs(i,j)=⎩
⎨
⎧minm=i+(k−1)x){dfs(i,m)+dfs(m+1,j)}+∑q=ijstones[q]minm=i+(k−1)x){dfs(i,m)+dfs(m+1,j)}(j−i)mod(k−1)=0(j−i)mod(k−1)=0
- 递归边界: d f s ( i , i ) = 0 dfs(i,i) =0 dfs(i,i)=0 ,只有一堆石头,无需合并,代价为 0 0 0
- 递归入口: d f s ( 0 , n − 1 ) dfs(0, n-1) dfs(0,n−1) ,把所有石头堆合并成一堆的最小代价
class Solution {
public:
int mergeStones(vector<int> &stones, int k) {
int n = stones.size();
if ((n - 1) % (k - 1)) return -1; // 无法合并成一堆
int s[n + 1];
s[0] = 0;
for (int i = 0; i < n; i++) s[i + 1] = s[i] + stones[i]; // 前缀和
int dp[n][n];
memset(dp, -1, sizeof(dp)); // -1 表示还没有计算过
function<int(int, int)> dfs = [&](int i, int j) -> int {
if (i == j) return 0; // 只有一堆石头,无需合并
int &ans = dp[i][j]; // 注意这里是引用,下面会直接修改 dp[i][j]
if (ans != -1) return ans;
ans = INT_MAX;
for (int m = i; m < j; m += k - 1) // 枚举哪些石头堆合并成第一堆
ans = min(ans, dfs(i, m) + dfs(m + 1, j));
if ((j - i) % (k - 1) == 0) ans += s[j + 1] - s[i]; // 可以合并成一堆
return ans;
};
return dfs(0, n - 1);
}
};
解法2 动态规划
把解法1的 d f s dfs dfs 改为 f f f 数组,把递归改为循环即可。需要注意循环的顺序:
- 由于 i < m + 1 i < m+1 i<m+1 , f [ i ] f[i] f[i] 要能从 f [ m + 1 ] f[m + 1] f[m+1] 转移过来,必须先计算出 f [ m + 1 ] f[m+1] f[m+1] ,所以 i i i 要倒序枚举;
- 由于 j > m j > m j>m , f [ i ] [ j ] f[i][j] f[i][j] 要能从 f [ i ] [ m ] f[i][m] f[i][m] 转移过来,必须先计算出 f [ i ] [ m ] f[i][m] f[i][m] ,所以 j j j 要正序枚举。
class Solution {
public:
int mergeStones(vector<int> &stones, int k) {
int n = stones.size();
if ((n - 1) % (k - 1)) return -1; // 无法合并成一堆
int s[n + 1];
s[0] = 0;
for (int i = 0; i < n; i++) s[i + 1] = s[i] + stones[i]; // 前缀和
int f[n][n];
for (int i = n - 1; i >= 0; --i) {
f[i][i] = 0;
for (int j = i + 1; j < n; ++j) {
f[i][j] = INT_MAX;
for (int m = i; m < j; m += k - 1)
f[i][j] = min(f[i][j], f[i][m] + f[m + 1][j]);
if ((j - i) % (k - 1) == 0) // 可以合并成一堆
f[i][j] += s[j + 1] - s[i];
}
}
return f[0][n - 1];
}
};
复杂度分析:
- 时间复杂度: O ( n 3 k ) O(\dfrac{n^3}{k}) O(kn3) ,其中 n n n 为 s t o n e s stones stones 的长度。这里状态个数为 n 2 n^2 n2 个,单个状态的计算时间为 O ( n k ) O(\dfrac{n}{k}) O(kn) ,因此时间复杂度为 O ( n 3 k ) O(\dfrac{n^3}{k}) O(kn3)
- 空间复杂度: O ( n 2 ) O(n^2) O(n2) 。
![【参考文献不爆红】Word的多个参考文献连续交叉引用([1] [3]改为[1-3])](https://img-blog.csdnimg.cn/4367f3ac93f742668beb11ec2c48d188.png)