深度学习 -- 张量操作与线性回归 张量的数学运算以及用张量构建线性回归模型

news2024/12/24 0:04:18

前言

这篇博客继承前篇博客的内容，将对张量的操作进行阐述，同时在理解张量的一些数学的基础上，配合机器学习的理论，在pytorch环境中进行一元线性回归模型的构建。

张量的拼接与切分

torch.cat()
功能：将张量按维度dim进行拼接

torch.stack()
功能：在新创建的维度dim上进行拼接

在这里插入图片描述

  • tensors：张量序列
  • dim：要拼接的维度
import torch
a = torch.ones((2,3))
# 张量的拼接
a1 = torch.cat([a,a],dim=0)
print(a)
print(a1)

输出：

tensor([[1., 1., 1.],
        [1., 1., 1.]])
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])

dim=1

a2 = torch.cat([a,a],dim=1)
print(a2)

tensor([[1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.]])

stack：

import torch
a = torch.ones((2,3))

a1 = torch.stack([a,a],dim=2)
print(a1)

输出：

tensor([[[1., 1.],
         [1., 1.],
         [1., 1.]],

        [[1., 1.],
         [1., 1.],
         [1., 1.]]])

torch.chunk()
功能：将张量按维度dim进行平均切分
返回值：张量列表
注意事项：若不能整除，最后一份张量小于其他张量

在这里插入图片描述

  • input：要切分的张量
  • chunks：要切分的份数
  • dim：要切分的维度
b = torch.ones((2,5))
print(b)
b1 = torch.chunk(b,dim=1,chunks=2)
print(b1)

输出：

tensor([[1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.]])
(tensor([[1., 1., 1.],
        [1., 1., 1.]]), tensor([[1., 1.],
        [1., 1.]]))

torch.split()
功能：将张量按维度dim进行切分
返回值：张量列表

在这里插入图片描述

  • tensor：要切分的张量
  • split_size_or_setions:为int时，表示每一份的长度；为list时，按lisr元素切分
  • dim：要切分的维度
c = torch.ones((2,5))
c1 = torch.split(c,2,dim=1)
print(c1)

(tensor([[1., 1.],
        [1., 1.]]), tensor([[1., 1.],
        [1., 1.]]), tensor([[1.],
        [1.]]))

采用list：

c = torch.ones((2,5))
c1 = torch.split(c,[2,1,2],dim=1)
# print(c1)
for i in c1:
    print(i)

tensor([[1., 1.],
        [1., 1.]])
tensor([[1.],
        [1.]])
tensor([[1., 1.],
        [1., 1.]])

注意：
list中所有的元素加起来需要等于指定维度上的张量的长度。

张量的索引

torch.index_select()
功能：在维度dim上，按index索引数据
返回值：依index索引数据拼接的张量
在这里插入图片描述

  • input:要索引的张量
  • dim：要索引的维度
  • index：要索引数据的序号
d = torch.randint(0,9,size=(3,3))
idx = torch.tensor([0,2],dtype=torch.long)
d1 = torch.index_select(d,dim=0,index=idx)
print(d)
print(idx)
print(d1)

输出：

tensor([[5, 0, 3],
        [1, 0, 3],
        [0, 8, 2]])
tensor([0, 2])
tensor([[5, 0, 3],
        [0, 8, 2]])

注意：
index的值需要是一个张量 而且dtype也必须是torch.long

torch.masked_select()
功能：按mask中的True进行索引
返回值：一维张量

在这里插入图片描述

  • input:要索引的张量
  • mask:与input同形状的布尔类型张量
t = torch.randint(0,9,size=(3,3))
mask = t.ge(5)
print(t)
print(mask)

ge(x)方法的使用：
当张量中的元素>=x的时候就会变True，剩余情况则为False，该例子中x是5.

t和mask的值：（每次都会变）

tensor([[0, 3, 6],
        [7, 5, 8],
        [2, 8, 0]])
tensor([[False, False,  True],
        [ True,  True,  True],
        [False,  True, False]])

使用masked_select(）方法进行布尔值为True的元素索引

t = torch.randint(0,9,size=(3,3))
mask = t.ge(5)
print(t)
print(mask)

t1 = torch.masked_select(t,mask=mask)
print(t1)

输出：

tensor([[8, 8, 4],
        [1, 4, 7],
        [6, 4, 5]])
tensor([[ True,  True, False],
        [False, False,  True],
        [ True, False,  True]])
tensor([8, 8, 7, 6, 5])

张量变换

torch.reshape()
功能：变换张量的形状
注意事项：当张量在内存中是连续时，新张量与input共享数据内存

在这里插入图片描述

  • input:要变换的张量
  • shape:新张量的形状
t = torch.ones(8)
t_reshape = torch.reshape(t,(2,4))
print(t)
print(t_reshape)

输出：

tensor([1., 1., 1., 1., 1., 1., 1., 1.])
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.]])

如果把原始张量的第一个元素改为2

t[0] = 2
print(t_reshape)

tensor([[2., 1., 1., 1.],
        [1., 1., 1., 1.]])

会发现改变过形状的张量的第一个元素也会改变，说明新张量与input共享数据内存。

注：共享数据内存不代表，它们在同一个内存地址，而是代表它们所指向的内存空间是一样的。

print(id(t),id(t_reshape)) # 2081724628720 2081889008512
print(id(t.data),id(t_reshape.data)) # 1370880600800 1370880600800

torch.transpose()
功能：交换张量的两个维度

torch.t()
功能：2维张量转置，对矩阵而言，等价于torch.transpose(input,0,1)

在这里插入图片描述

  • input:要交换的张量
  • dim0：要交换的维度
  • dim1：要交换的维度
t = torch.rand(size=(2,3,4))
print(t)
t1 = torch.transpose(t,0,1)
print(t1)

tensor([[[0.6628, 0.1919, 0.1204, 0.3246],
         [0.0973, 0.0540, 0.3222, 0.4540],
         [0.2753, 0.3575, 0.4117, 0.2105]],

        [[0.0800, 0.7416, 0.3095, 0.6480],
         [0.9503, 0.8973, 0.0828, 0.2698],
         [0.6524, 0.1959, 0.3461, 0.8498]]])
tensor([[[0.6628, 0.1919, 0.1204, 0.3246],
         [0.0800, 0.7416, 0.3095, 0.6480]],

        [[0.0973, 0.0540, 0.3222, 0.4540],
         [0.9503, 0.8973, 0.0828, 0.2698]],

        [[0.2753, 0.3575, 0.4117, 0.2105],
         [0.6524, 0.1959, 0.3461, 0.8498]]])

Process finished with exit code 0

torch.squeeze()
功能：压缩维长度为1的维度（轴）

  • dim：若为None，移出所有长度为1 的轴；若指定维度，当且仅当该轴长度为1时，可以被移除；

torch.unsqueeze()
功能：依据dim扩展维度

  • dim：扩展的维度

在这里插入图片描述

t = torch.rand((1,2,3,1))
print(t.shape)
t1 = torch.squeeze(t)
print(t1.shape)

输出：

torch.Size([1, 2, 3, 1])
torch.Size([2, 3])

如果指定了dim参数：

t = torch.rand((1,2,3,1))
print(t.shape)
t1 = torch.squeeze(t,dim=0)
print(t1.shape)

输出：

torch.Size([1, 2, 3, 1])
torch.Size([2, 3, 1])

就只会压缩第四维度的轴。

张量的数学运算

pytorch中提供了丰富的张量数学运算

1、加减乘除

  • torch.add()
  • torch.addcdiv()
  • torch.addcmul()
  • torch.sub()
  • torch.div()
  • torch.mul()

2、对数，指数，幂函数

  • torch.log(input,out=None)
  • torch.log10(input,out=None)
  • torch.log2(input,out=None)
  • torch.exp(input,out=None)
  • torch.pow()

3、三角函数

  • torch.abs(input,out=None)
  • torch.acos(input,out=None)
  • torch.cosh(input,out=None)
  • torch.cos(input,out=None)
  • torch.asin(input,out=None)
  • torch.atan(input,out=None)
  • torch.atan2(input,out=None)

torch.add()
功能：逐元素计算 input + alpha x other

在这里插入图片描述

  • input:第一个张量
  • alpha:乘项因子
  • other:第二个张量

add()方法不仅仅可以做加法运算，还可以做线性运算

  • 机器学习中的公式：
    y = wx + b
import torch
# torch.add()

t = torch.rand((3,3))
t1 = torch.rand((3,3))
print("t",t)
print("t1",t1)
t2 = torch.add(t,t1)
t3 = torch.add(t,t1,alpha=2)
print("t2",t2)
print("t3",t3)

输出：

t tensor([[0.8218, 0.8576, 0.4829],
        [0.6046, 0.1290, 0.4835],
        [0.5752, 0.2386, 0.1260]])
t1 tensor([[0.5306, 0.7424, 0.4328],
        [0.3278, 0.1980, 0.4354],
        [0.4742, 0.4319, 0.8922]])
t2 tensor([[1.3524, 1.6000, 0.9157],
        [0.9324, 0.3270, 0.9189],
        [1.0494, 0.6705, 1.0182]])
t3 tensor([[1.8830, 2.3423, 1.3484],
        [1.2602, 0.5249, 1.3544],
        [1.5236, 1.1024, 1.9104]])

线性回归

线性回归时分析一个变量与另外一（多）个变量之间关系的 方法

因变量：y
自变量：x
关系：线性

y = wx + b

分析：求解w，b

求解步骤：
1、确定模型
Model: y = wx + b

2、选择损失函数
MSE: 均方差
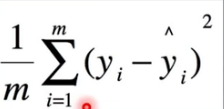
在这里插入图片描述

3、求解梯度并更新w，b
w = w - LRw.grad
b = b - LRw.grad

pytorch中实现一元线性回归模型

# 一元线性回归
import torch
import matplotlib.pyplot as plt

torch.manual_seed(10)

lr = 0.1 #学习率/步长

# 创建训练数据
x = torch.rand(20,1) * 10
y = 2*x + (5 + torch.randn(20,1))

# 构建线性回归参数
w = torch.randn((1),requires_grad=True) # 允许更新梯度
b = torch.zeros((1),requires_grad=True)

for iteration in range(1000):
    # 前向传播
    wx = torch.mul(w,x)
    y_pred = torch.add(wx,b)

    # 计算MSE loss
    loss = (0.5*(y-y_pred)**2).mean()

    # 反向传播
    loss.backward()

    # 更新参数
    w.data.sub_(lr * w.grad)
    b.data.sub_(lr * b.grad)

    if iteration % 20 == 0:
        plt.scatter(x.data.numpy(),y.data.numpy())
        plt.plot(x.data.numpy(),y_pred.data.numpy(),'r-',lw=5)
        plt.text(2,20,'Loss=%.4f' % loss.data.numpy())
        plt.xlim(1.5,10)
        plt.ylim(8,28)
        plt.title("huiguimoxing interation={}".format(iteration))
        plt.pause(0.5)
        plt.show()

        if loss.data.numpy() < 1:
            break

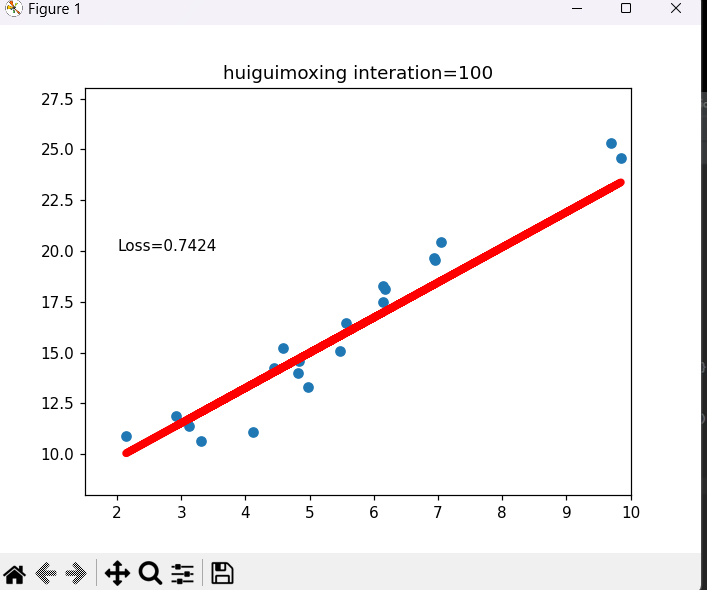
在这里插入图片描述

当迭代到100次时loss已经接近0了 此时该线性的图也接近这些这些数据。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/448553.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Node.js四：包管理工具

Node.js四：包管理工具

1.介绍 2.npm安装 3.npm基本使用 属性翻译 4.搜索下载安装包 npm搜索网站&#xff1a; npm 5.生产环境与开发环境 开发环境 是程序员 专门用来写代码 的环境&#xff0c;一般是指程序员的电脑&#xff0c;开发环境的项目一般 只能程序员自己访问 生产环境 是项目 代码正式运行 …
阅读更多...
海光信息业绩高歌猛进，但其作为国产CPU龙头的“地基”并不牢固

海光信息业绩高歌猛进，但其作为国产CPU龙头的“地基”并不牢固

‍数据智能产业创新服务媒体 ——聚焦数智 改变商业 在“芯片寒冬”的大背景下&#xff0c;2022年全球头部芯片半导体公司纷纷下调业绩预期&#xff0c;英特尔、英伟达、美光等无一幸免。但是随着AIGC异军突起&#xff0c;仿佛寒冬中的一股暖流&#xff0c;催生着半导体市场行…
阅读更多...
第四章 面向对象(OOP)

第四章 面向对象(OOP)

目录 一、编程思想 1.1. 面向对象 1.2. 面向过程 1.3.举例说明&#xff08;把大象装进冰箱&#xff09; 1.4.二者的联系与区别 1.5.面向对象的三个阶段 1.6.什么是类&#xff0c;什么是实例&#xff0c;二者的联系 二、面向对象三大特征 2.1 封装 2.2 继承 2.3 多态…
阅读更多...
go-zero入门

go-zero入门

文章目录 简介框架设计环境准备go安装Go Module设置goctl安装安装(mac\&linux)安装(windows) protoc & protoc-gen-go安装 goctl 各层代码生成一览goctl 生成REST和RPC微服务生成数据模型层Model生成API服务目录结构开发者需要做的修改配置文件修改上下文依赖修改业务逻…
阅读更多...
CMake基本使用

CMake基本使用

重要指令 cmake_minimum_required:指定CMake最小版本要求 project&#xff1a;定义工程名称&#xff0c;并可指定语言 set&#xff1a;显示的定义变量 include_directories&#xff1a;向工程添加多个特定头文件搜素路径 link_directories&#xff1a;向工程添加多个特定库文件…
阅读更多...
Spring lettuce读写分离

Spring lettuce读写分离

Redis 的 Sentinel 模式默认配置下 Redis 的客户端只对 Master 读写&#xff0c;另外2个Slave闲置。若主从节点在不同机房&#xff0c;在读取时会有跨机房的网络时延&#xff0c;并且比同机房访问更容易发生网络丢包。故在一些场景可以考虑将跨机房的服务节点设置为读写分离 Re…
阅读更多...
计算机组成原理——第五章中央处理器（下）

计算机组成原理——第五章中央处理器（下）

梦里不知身是客&#xff0c;一晌贪欢 文章目录 5.6.1 指令流水线的基本概念5.6.2 指令流水线的影响因素和分类五段式指令流水线5.7.1 多处理器的基本概念5.7.2 硬件多线程的基本概念 5.6.1 指令流水线的基本概念 想要对指令的过程进行优化&#xff0c;一条指令的执行过程可以被…
阅读更多...
世界新冠疫情数countrydata.csv 表，实战分析

世界新冠疫情数countrydata.csv 表，实战分析

一、环境要求 Hadoop hive spark hbase开发环境 开启hadoop&#xff1a;start-all.sh开启zookeeper&#xff1a;zkServer.sh start开启hive&#xff1a;nohup hive --service metastore &nohup hive --service hiveserver2 & 打开hive界面&#xff1a;beeline -u …
阅读更多...
单列集合之Set集合以及各种实现类

单列集合之Set集合以及各种实现类

Set集合 Set接口也是Collection单列结合的一个子接口&#xff0c;set集合中没有提供其他额外的方法&#xff0c;但是相比较Collection集合新增了其他的特性。所有实现了Set接口的类都可以叫做Set集合。 Coliection接口中的方法&#xff1a;Collection集合的方法 Set集合不允…
阅读更多...
更全面的对比GPT4和Claude对MLIR的掌握能力

更全面的对比GPT4和Claude对MLIR的掌握能力

本文构造了20个MLIR基础概念的问题以及使用OneFlow IR转换为Tosa IR的5个代码段来评测GPT4和Claude对于MLIR的掌握能力&#xff0c;我的结论是对于基础概念的理解Claude整体上和GPT4持平&#xff0c;而在阅读相关代码片段时Claude表现出了比GPT4更强一点的理解能力。 0x0. 前言…
阅读更多...
【Python】读取r语言数据+NMF算法（完整代码+详细注释）

【Python】读取r语言数据+NMF算法（完整代码+详细注释）

目录 依赖库代码功能完整代码总结 欢迎关注 『Python』 系列&#xff0c;持续更新中 欢迎关注 『Python』 系列&#xff0c;持续更新中 算法部分源码是我的数模兄弟想要深入研究nmf算法方面的内容发给我让我跑的 参考自博文 https://blog.csdn.net/atease0001/article/details/…
阅读更多...
计及光伏电站快速无功响应特性的分布式电源优化配置方法（Matlab代码实现）

计及光伏电站快速无功响应特性的分布式电源优化配置方法（Matlab代码实现）

&#x1f4a5; &#x1f4a5; &#x1f49e; &#x1f49e; 欢迎来到本博客 ❤️ ❤️ &#x1f4a5; &#x1f4a5; &#x1f3c6; 博主优势&#xff1a; &#x1f31e; &#x1f31e; &#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 …
阅读更多...
JS的函数定义和参数

JS的函数定义和参数

文章目录 一、JavaScript 函数定义二、JavaScript 函数参数总结 一、JavaScript 函数定义 JavaScript 使用关键字 function 定义函数。 函数可以通过声明定义&#xff0c;也可以是一个表达式。 函数声明 function functionName(parameters) {执行的代码 }函数声明后不会立即…
阅读更多...
【C++内联函数】

【C++内联函数】

目录 前言内联函数的概念内联函数的特性内联函数的总结 前言 假设有这样的一个场景&#xff0c;有一个代码量不足三行的函数被调用了一万次&#xff0c;现在让你做优化&#xff0c;你会怎么考虑优化&#xff1f; 我们都知道函数调用是有时间和空间开销的。程序在执行一个函数之…
阅读更多...
Ansys Lumerical | 使用 STACK 仿真抗反射偏振器件

Ansys Lumerical | 使用 STACK 仿真抗反射偏振器件

1、说明 在本示例中&#xff0c;我们将展示使用 Lumerical STACK 求解器来设计抗反射圆偏振器&#xff0c;以减少 OLED 显示器的环境光反射。 2、综述 OLED 显示器的底部金属电极可以用于增强光提取效率&#xff0c;然而它也会带来环境光反射的不利影响&#xff0c;导致显示器在…
阅读更多...
深度学习-基础（二）-numpy中的轴操作

深度学习-基础（二）-numpy中的轴操作

背景 使用Pytorch进行学习&#xff0c;少不了跟numpy打交道&#xff0c;比如数据集中去除通道reduction只有做加法运算等&#xff0c;但是numpy轴操作&#xff0c;很少有人讲清楚&#xff0c;此处加以梳理。 轴的概念 轴用来为超过一维的数组定义的属性&#xff0c;二维数据…
阅读更多...
【Atlas500】华为500小站预配置

【Atlas500】华为500小站预配置

目录 基础配置解决配置能力项未开启问题 基础配置 1.网线连接盒子 2.1口IP:192.168.2.111 2口IP&#xff1a;192.168.3.111 3.登临网页https://192.168.2.111 输入用户名和密码&#xff08;管理端用户&#xff09;。 ● 默认用户名&#xff1a;admin ● 默认密码&#xff1a;H…
阅读更多...
Eclipse安装插件及所有插件下载地址汇总

Eclipse安装插件及所有插件下载地址汇总

Eclipse安装插件及所有插件下载地址汇总 插件的意义安装插件各插件下载地址汇总kepler&#xff08;Eclipse配置本地安装好的Tomcat时使用的插件&#xff09;另一个插件名称 插件的意义 自认是为了解耦&#xff0c;使使用eclipse的人可以依据自己所需&#xff0c;有针对性的下载…
阅读更多...
MySQL_第04章_运算符

MySQL_第04章_运算符

第04章_运算符 讲师&#xff1a;尚硅谷 - 宋红康&#xff08;江湖人称&#xff1a;康师傅&#xff09; 官网&#xff1a; http://www.atguigu.com 1. 算术运算符 算术运算符主要用于数学运算&#xff0c;其可以连接运算符前后的两个数值或表达式&#xff0c;对数值或表达式…
阅读更多...
Node第三方包 【mysql2】

Node第三方包 【mysql2】

文章目录 &#x1f31f;前言&#x1f31f;访问数据库&#x1f31f;MySQL驱动&#x1f31f;mysql2&#x1f31f;安装 &#x1f31f;方法&#x1f31f;连接数据库&#x1f31f;通过 query() 方法执行SQL语句&#x1f31f;通过 execute() 方法执行SQL语句 &#x1f31f;使用连接池…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023