霍夫变换是1962年由霍夫发明的一种检测图像中直线、圆等形状的方法。后来1972年经过Richard O. Duda和Peter E. Hart改进,形成了今天的霍夫变换算法。
今天我就带大家了解了解霍夫变换之直线检测是怎么特么的一回事。
1.霍夫变换
说到霍夫变换,首先就得说说坐标系的事情,虽然这都是初、高中的知识了,但经过大学几年的洗刷,不知道各位还能记住多少。为了使大家的远古记忆觉醒,我就领大家回忆回忆!
首先是直线的直角坐标系方程(以x,y为坐标轴),y=k*x+b,不知道还记不记得?k是斜率,b是直线与y轴的交点,x、y是变量,如图1所示:
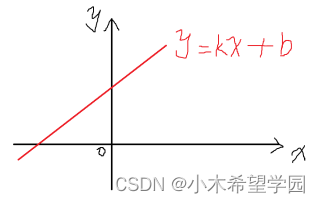
图1
如果我们已知图像上面任意两个点,系数k,b就能够确定,那么方程就可以写成图2的形式。
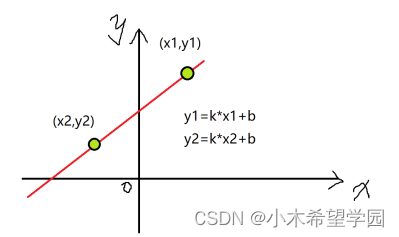
图2
我们确定了k,b之后得到(k1,b1),把它作为一个点的位置,画到另外一个以k,b为坐标轴的直角坐标系中,我们就会得到图3,图3的直角坐标系我们就称为霍夫空间。
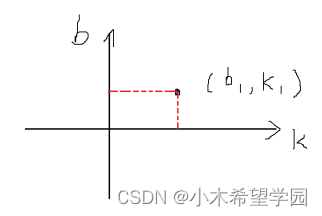
图3
假定霍夫空间中有一条线,它的方程为b=-x3*k+y3,也就是y3=k*x3+b。那么它对应的x,y直角坐标系就是一个点(x3,y3),如图4。反过来也可以说,直角坐标系中的一个点,就是霍夫空间中的一条直线。
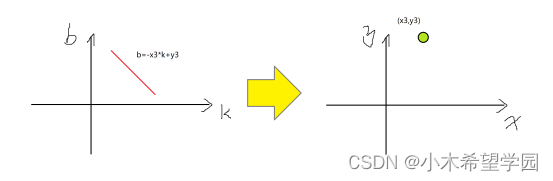
图4
霍夫空间有一个定理:假定直角坐标系有N个点,如果这N个点能够在直角坐标系中连成一条直线,那么它们在霍夫空间中就会交于一点。
假如N=3,有三个点,分别是(1,2),(2,4),(3,6),这三个点在直角坐标系中可以连成一条直线y=2*x,我们看图5,他们在霍夫空间中肯定会交于一点。
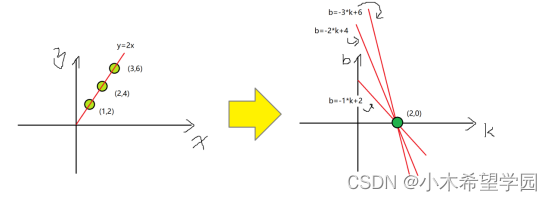
图5
但是在我们计算机视觉里面,很少有人使用直角坐标系来解决问题,而使用极坐标。其原因是当直角坐标系的直线垂直于x轴时,k为无穷大。这很难在计算机中表示,使用极坐标就能够很好的解决这个问题。极坐标方程如图6所示,ρ代表长度,θ代表角度。这个怎么来的呢,假如我们有一点(x4,y4),它的极坐标求法看图7,一下就明白了。
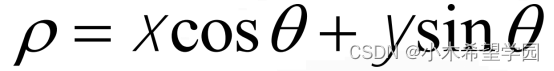
图6
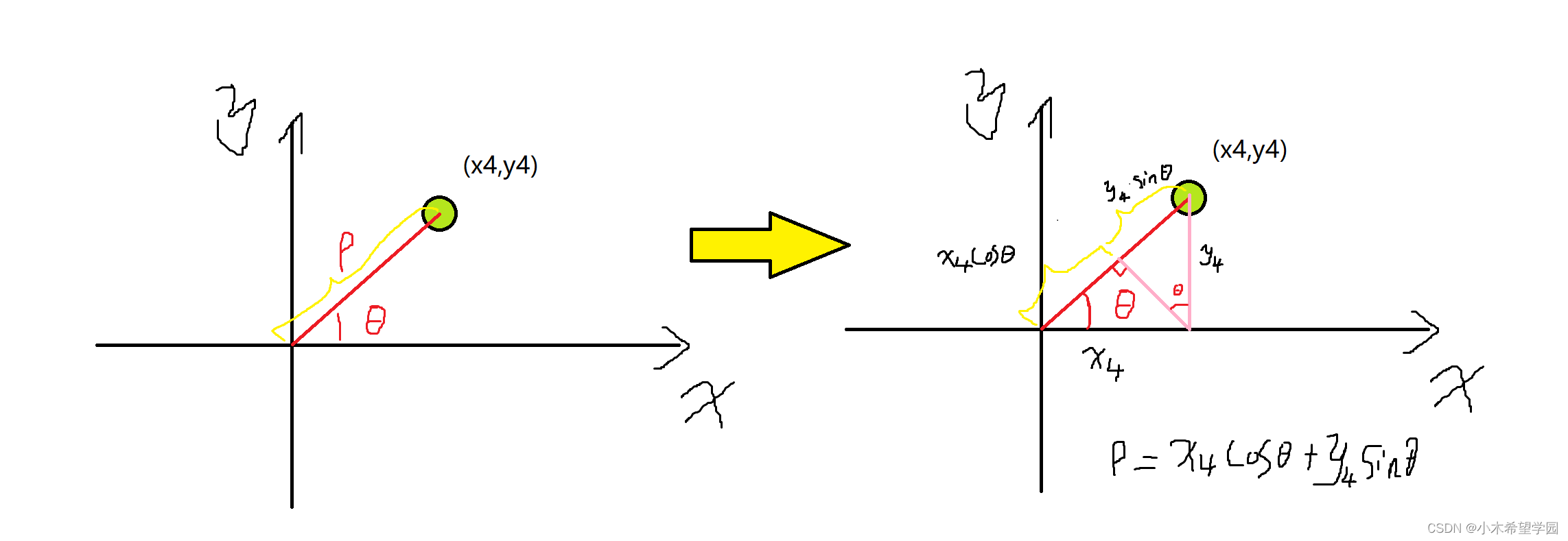
图7
直角坐标系的一点(x4,y4),对应极坐标系下的一条正弦曲线ρ4=x4*cosθ4+y4*sinθ4,我们称这个极坐标系为“极坐标霍夫空间”,盗用别人一张图:
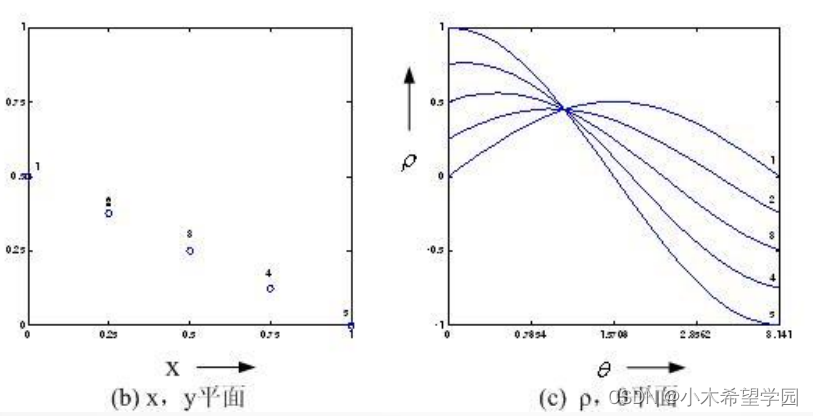
图8
我们根据上面的原理,直角坐标系有N个点,如果这N个点能够在直角坐标系中连成一条直线,那么它们在霍夫空间中肯定会交于一点。在“极坐标霍夫空间”中也是一样,只是变为曲线交于一点,如图8所示。
这样,我们就把直角坐标系的点,变换到极坐标霍夫空间中了。
2.直线检测
我们想象一下,如图8所示,如果有三个点,这三个点在霍夫空间的曲线是交于一点的,那么三个点肯定在一条直线上。我们通过这个原理就可以对直线进行检测了。
首先我们第一步需要把一张图的边缘给勾勒出来,比如使用canny边缘检测算法。
接下来,我们来检测边缘中那些是直线。为了简化问题,我们拿一条直线作为边缘来举例。这条直线如图9所示,
- 将空间量化成许多小格,绿色的字代表X,Y坐标。黑色为边缘点,是由8个像素点组成。白色为非边缘点(在这里我们不予考虑)
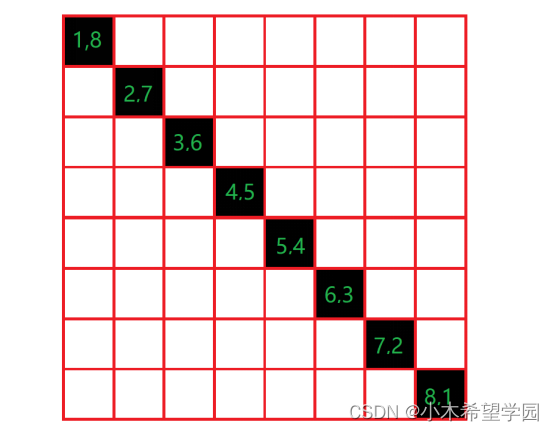
图9
2. 假设我们的像素分辨率为1,θ变换角度变换的分辨率为45°,那么我们就对全部8个黑色的点进行极坐标霍夫变换, 变换后我们会得到8条曲线,如第一条曲线是ρ=cosθ+8*sinθ,接下来我们根据曲线求θ=0、45、90、135、180° 的ρ值,用公式ρ=x*cosθ+y*sinθ计算,一共8*8=64个数。计算结果如图10所示(横向代表5个角度,纵向代表从(1,8)到(8,1)的8个像素点,值为ρ)
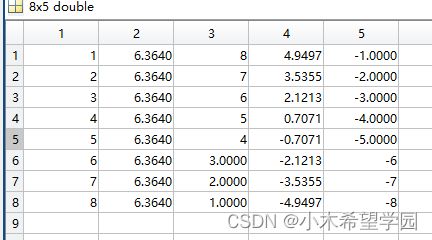
图10
3. 计算完成后,我们发现θ=45°时候,ρ=6.3640数目最多,为8个,别的θ对应的ρ值数目均小于8个,因此,直线的极坐标方程为 6.3640=x*cos45°+y*sin45°,到此该直线方程就求出来了。我们换算成直角坐标系,在画出线段来即可。
3.一个实例
举个例子,我们图11(a)是一张原图,我们通过第五节讲过的canny算法,把边缘勾勒出来,如图9(b)所示:
白话文讲计算机视觉-第五讲-canny边缘检测算法_小木希望学园的博客-CSDN博客
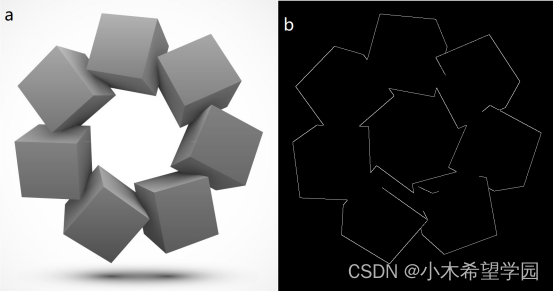
图11
接下来,我们通过一条python语句来进行霍夫变换直线检测:
lines=cv2.HoughLinesP(edges, rho, theta, threshold, np.array([]), min_line_length, max_line_gap)我们需要在找到一个边缘图中值为1的点(X1,Y1)(0为背景,1为边缘),设定像素分辨率为rho,也就是说我们沿着某一个方向(可以是0°,±45°,±90°,180°等等),一次走一个格子,一直走下去,看看能不能和这个(X1,Y1)点连成一条直线。
那么我们沿着某一个方向怎么确定呢,很简单,再设定一个角度分辨率theta,就是我们可以沿着哪一个方向的角度行走,如果为1的话,走的方向可以是(0,1,2,3,。。。,180度)。
我们继续设定一个参数threshold——检测一条直线所需最少的交点,假如我们设定该值为20,我们沿着这个角度一直往前走,走20个点之后,我们如果发现20个点在该方向处的极坐标ρ值都与(X1,Y1)相同,那么我们就认为它是一条直线,如果没到20个点值就变了,就不认为这是一条直线了。
上述情况中,max_line_gap这个值为1,也就是走一个格子检测一下是否有极坐标值交点(ρ值相同),如果要是max_line_gap这个值不为1,为5,那就是说,我沿着这个角度一直往前走,先走5个点,如果这5个点中有2个点和(X1,Y1)的ρ值相同,那么就可以认为是一条直线,然后我们接着往下面走,再走5个点走到第10个点后,里面需要再有一个点和(X1,Y1)的ρ值相同;再走5个点到第15个点,里面需要再有一个点和(X1,Y1)的ρ值相同,依次类推继续前进,直到有20个点和(X1,Y1)的ρ值相同即可认为是一条直线;当小于20个点时,走5个点之后没有点相交就不认为是直线。
我们把所有的边缘点进行霍夫变换,把所有的角度都给遍历了,我们就会得到一堆线段。
我们设定变量min_line_length,表示组成一条直线的最少点的数量。比如我们设定和threshold相同或者小于threshold,那么我们就不舍弃任何一个点。如果设定比threshold大,如为50,就舍弃一些直线像素点数小于50个的就不要了。
最后线段的坐标保存在line中。
我们的参数设定为:
rho = 1 # 像素分辨率(1 pix)
theta = np.pi / 180 # 角度分辨率(1度)
threshold = 20 # 检测一条直线所需最少的交点
min_line_length = 50 # 组成一条直线的最少点的数量
max_line_gap = 20 # 能被认为在一条直线上的亮点的最大距离最终获得的图像如图12所示,检测的线段效果还行,有些遗漏,有些误检,这需要慢慢调参数来优化。

图12
以下是python的代码:
# 导入类库
import cv2
import numpy as np
if __name__ == '__main__':
# 读入灰度图片
img = cv2.imread("linetest.jpg", 0)
# 显示图片
cv2.imshow('orgin', img)
# 进行边缘检测,设定高低阈值分别为50,75。后把canny边缘图片保存到硬盘,名字为canny.jpg
edges = cv2.Canny(img, 50, 75)
# 保存图片
cv2.imwrite("canny.jpg", edges)
# 显示边缘图片
cv2.imshow("canny", edges)
# 输入霍夫变换参数
rho = 1 # 像素分辨率(1 pix)
theta = np.pi / 180 # 角度分辨率(1度)
threshold = 20 # 检测一条直线所需最少的交点
min_line_length = 50 # 组成一条直线的最少点的数量
max_line_gap = 20 # 能被认为在一条直线上的亮点的最大距离
# 创建一张新图
line_image = cv2.imread("linetest.jpg")
# 霍夫检测函数
lines = cv2.HoughLinesP(edges, rho, theta, threshold, np.array([]), min_line_length, max_line_gap)
# 把线段画到line_image上面
for line in lines:
for x1, y1, x2, y2 in line:
cv2.line(line_image, (x1, y1), (x2, y2), (0, 0, 255), 5) # 5代表粗细
# 显示直线检测图片
cv2.imshow("Hough", line_image)
# 保存图片
cv2.imwrite("Hough.jpg", line_image)
# 按任意键退出
cv2.waitKey()
cv2.destroyAllWindows()
PS:直线检测是所有的点在极坐标空间交于一点,我们利用同样的方法可以检测圆形,方法是“所有的点到某一定点的距离都是同一个值”。大家可以自己继续琢磨琢磨看。
霍夫变换直线检测到这里就结束啦,谢谢大家!